Dos masas unidas en un aro

De Laplace

Contenido

1 Enunciado
2 Posiciones, velocidades y aceleraciones
3 Velocidad angular
4 Momento cinético y energía cinética
- 4.1 Momento cinético
- 4.2 Energía cinética
5 Fuerzas y momentos

1 Enunciado

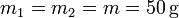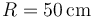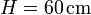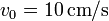Dos pequeñas masas iguales $m_1=m_2=m=50\,\mathrm{g}$ se encuentran ensartadas en un aro circular de radio $R=50\,\mathrm{cm}$ (de masa despreciable). Las masas están unidas entre sí por una varilla rígida de longitud $H=60\,\mathrm{cm}$ y masa despreciable. La masa $m 1$ se mueve en todo momento con rapidez $v_0=10\,\mathrm{cm}/\mathrm{s}$ .

Empleando el sistema de ejes de la figura en el que el eje OX es ortogonal a la varilla, determine las posiciones, velocidades y aceleraciones de ambas masas y del centro de masas del sistema.
Calcule la velocidad angular del sistema de dos masas.
Halle el momento cinético y la energía cinética del sistema respecto al centro del aro y respecto al centro de masas.
Calcule la fuerza que el aro ejerce sobre cada una de las masas. Determine la resultante y el momento resultante de estas fuerzas respecto al centro del anillo y respecto al centro de masas.

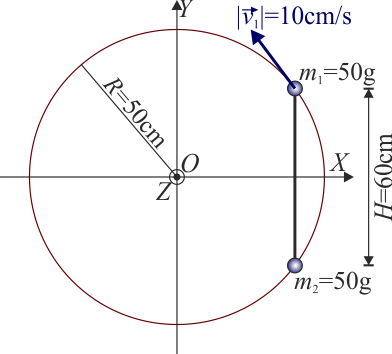
2 Posiciones, velocidades y aceleraciones

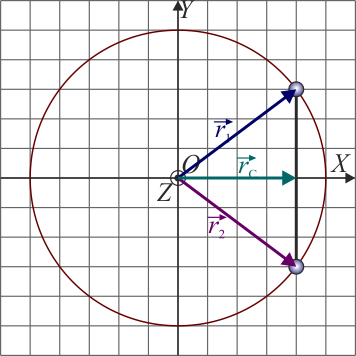
2.1 Posiciones

Obtenemos las tres posiciones casi por simple inspección.

Masa 1: Conocemos su coordenada $y$ , ya que por simetría, el OX pasa por el centro de la varilla

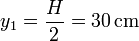
$y_1 = \frac{H}{2}=30\,\mathrm{cm}$

y calculamos su coordenada

x

aplicando el teorema de Pitágoras

$x = \sqrt{50^2-30^2}\,\mathrm{cm} = 40\,\mathrm{cm}$

lo que nos da el vector de posición

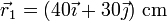
$\vec{r}_1 = \left(40\vec{\imath}+30\vec{\jmath}\right)\,\mathrm{cm}$

Masa 2: Su posición es la simétrica de la 1.

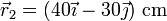
$\vec{r}_2 = \left(40\vec{\imath}-30\vec{\jmath}\right)\,\mathrm{cm}$

Centro de masas: Por ser las dos masas iguales, el CM está en el punto medio entre las dos

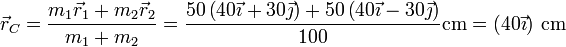
$\vec{r}_C = \frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}=\frac{50\left(40\vec{\imath}+30\vec{\jmath}\right)+50\left(40\vec{\imath}-30\vec{\jmath}\right)}{100}\mathrm{cm}=\left(40\vec{\imath}\right)\,\mathrm{cm}$

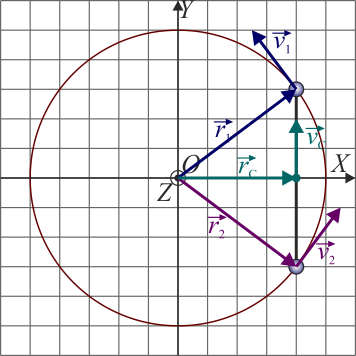
2.2 Velocidades

De la masa 1 conocemos su rapidez

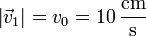
$\left|\vec{v}_1\right|=v_0 = 10\,\frac{\mathrm{cm}}{\mathrm{s}}$

De esta masa sabemos describe una trayectoria circular alrededor del origen, por lo que su velocidad cumple

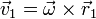
$\vec{v}_1 = \vec{\omega}\times\vec{r}_1$

siendo la velocidad angular en la dirección del eje de giro

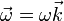
$\vec{\omega} = \omega\vec{k}$

El valor de esta velocidad angular es

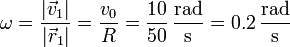
$\omega = \frac{|\vec{v}_1|}{|\vec{r}_1|}= \frac{v_0}{R}=\frac{10}{50}\,\frac{\mathrm{rad}}{\mathrm{s}} = 0.2\,\frac{\mathrm{rad}}{\mathrm{s}}$

y esto nos da la velocidad lineal, en cm/s

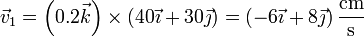
$\vec{v}_1=\left(0.2\vec{k}\right)\times(40\vec{\imath}+30\vec{\jmath}) = \left(-6\vec{\imath}+8\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

Operando igualmente obtenemos la velocidad de la segunda masa, que describirá otro movimiento circular con la misma velocidad angular

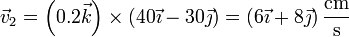
$\vec{v}_2=\left(0.2\vec{k}\right)\times(40\vec{\imath}-30\vec{\jmath}) = \left(6\vec{\imath}+8\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

La velocidad del CM es, como la posición, la media aritmética de las dos velocidades

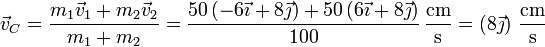
$\vec{v}_C = \frac{m_1\vec{v}_1+m_2\vec{v}_2}{m_1+m_2}=\frac{50\left(-6\vec{\imath}+8\vec{\jmath}\right)+50\left(6\vec{\imath}+8\vec{\jmath}\right)}{100}\,\frac{\mathrm{cm}}{\mathrm{s}}=\left(8\vec{\jmath}\right)\,\frac{\mathrm{cm}}{\mathrm{s}}$

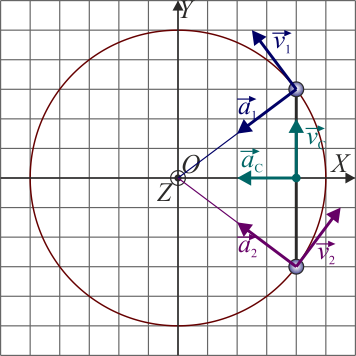
2.3 Aceleraciones

El movimiento circular de la masa 1 es uniforme, con rapidez constante. Por tanto, su aceleración es puramente normal e igual en módulo a

$a_1 = \frac{v_0^2}{R}=\omega^2 R$

Su dirección será radial y hacia adentro, lo que se puede escribir en forma vectorial

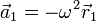
$\vec{a}_1 = -\omega^2\vec{r}_1$

y lo mismo para la masa 2. Esto nos da las aceleraciones, en cm/s²

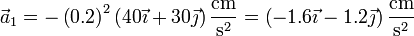
$\vec{a}_1 = -\left(0.2\right)^2\left(40\vec{\imath}+30\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}^2} = \left(-1.6\vec{\imath}-1.2\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}^2}$

y para la masa 2 será la simétrica

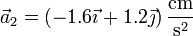
$\vec{a}_2 = \left(-1.6\vec{\imath}+1.2\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}^2}$

La aceleración del CM es la media de estas dos

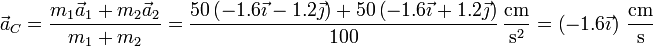
$\vec{a}_C = \frac{m_1\vec{a}_1+m_2\vec{a}_2}{m_1+m_2}=\frac{50\left(-1.6\vec{\imath}-1.2\vec{\jmath}\right)+50\left(-1.6\vec{\imath}+1.2\vec{\jmath}\right)}{100}\,\frac{\mathrm{cm}}{\mathrm{s}^2}=\left(-1.6\vec{\imath}\right)\,\frac{\mathrm{cm}}{\mathrm{s}}$

3 Velocidad angular

El centro instantáneo de rotación del sólido formado por las dos masas y la varilla es el origen O, ya que en él se cortan las dos perpendiculares a las velocidades. Por tanto, la velocidad de cada punto del sólido (incluyendo su CM) se puede escribir

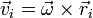
$\vec{v}_i = \vec{\omega}\times\vec{r}_i$

Esta es justamente la relación que empleamos antes para hallar la velocidad de la masa 1. Por tanto, no hace falta volver a hallar la velocidad angular. La que tiene en la partícula en su movimiento circular es la misma que la que tiene el sólido en su movimiento de rotación:

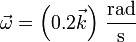
$\vec{\omega} = \left(0.2\vec{k}\right)\,\frac{\mathrm{rad}}{\mathrm{s}}$

4 Momento cinético y energía cinética

4.1 Momento cinético

El momento cinético respecto al origen es la suma de los momentos cinéticos individuales

$\vec{L}_O = m_1\vec{r}_1\times\vec{v}_1+m_2\vec{r}_2\times\vec{v}_2=50\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 40 & 30 & 0 \\ -6 & 8 & 0 \end{matrix}\right|+50\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 40 & -30 & 0 \\ 6 & 8 & 0 \end{matrix}\right| = \left(50000\vec{k}\right)\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

Este momento cinético se puede descomponer como

$\vec{L}_O = M\vec{r}_C\times\vec{v}_C+\vec{L}_C$

y de aquí despejamos el momento cinético respecto al centro de masas

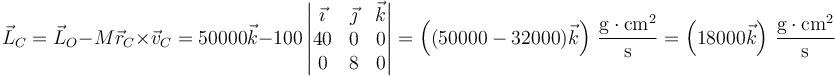
$\vec{L}_C=\vec{L}_O-M\vec{r}_C\times\vec{v}_C = 50000\vec{k}-100\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 40 & 0 & 0 \\ 0 & 8 & 0 \end{matrix}\right|=\left((50000-32000)\vec{k}\right)\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}= \left(18000\vec{k}\right)\,\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}}$

Estos dos momentos cinéticos pueden calcularse también según la fórmula

$\vec{L}_O = I_O\vec{\omega}\qquad \vec{L}_C = I_C\vec{\omega}$

siendo los momentos de inercia las sumas de las masas multiplicadas por las distancias al cuadrado al punto O y al CM respectivamente

$I_O = mR^2+mR^2 = 2(50\mathrm{g})\left(50\,\mathrm{cm}\right)^2=250000\,\mathrm{g}\cdot\mathrm{cm}^2\qquad\qquad I_C = my_1^2+my_2^2 = 2(50\mathrm{g})\left(30\,\mathrm{cm}\right)^2=90000\,\mathrm{g}\cdot\mathrm{cm}^2$

4.2 Energía cinética

Como con el momento cinético, la energía cinética es la suma de las de las dos partículas

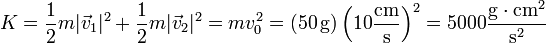
$K = \frac{1}{2}m|\vec{v}_1|^2+\frac{1}{2}m|\vec{v}_2|^2 = mv_0^2 = (50\,\mathrm{g})\left(10\frac{\mathrm{cm}}{\mathrm{s}}\right)^2 = 5000\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}$

Esta energía cinética puede también descomponerse en dos partes

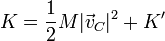
$K = \frac{1}{2}M|\vec{v}_C|^2+K'$

y de aquí despejamos la energía cinética respecto al centro de masas

$K' = K-\frac{1}{2}M|\vec{v}_C|^2 = 5000\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}-\frac{1}{2}\left(100\,\mathrm{g}\right)\left(8\frac{\mathrm{cm}}{\mathrm{s}}\right)^2 = \left(5000-3200\right)\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2} = 1800\frac{\mathrm{g}\cdot\mathrm{cm}^2}{\mathrm{s}^2}$

Estas dos energías cinéticas puedes también calcularse a partir de los momento de inercia hallados anteriormente

$K=\frac{1}{2}I_O|\vec{\omega}|^2 \qquad\qquad K'=\frac{1}{2}I_C |\vec{\omega}|^2$

5 Fuerzas y momentos

La fuerza neta sobre la masa 1 es, de acuerdo con la segunda ley de Newton

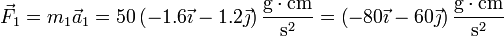
$\vec{F}_1 = m_1\vec{a}_1 = 50\left(-1.6\vec{\imath}-1.2\vec{\jmath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}^2} = \left(-80\vec{\imath}-60\vec{\jmath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}^2}$

Esta fuerza es suma vectorial de la reacción del anillo con la tensión de la varilla

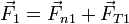
$\vec{F}_1 = \vec{F}_{n1}+\vec{F}_{T1}$

La reacción del anillo es puramente normal, mientras que la tensión de la varilla debe ir en la dirección de esta. Sin embargo, en este caso la suma de los dos vectores da como resultado un vector que es perpendicular al aro, es decir, va en la dirección de $\vec{F}_n$ . Concluimos entonces que la tensión de la varilla es nula y la fuerza de reacción del aro es toda la fuerza

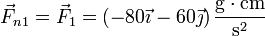
$\vec{F}_{n1} =\vec{F}_1=\left(-80\vec{\imath}-60\vec{\jmath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}^2}$

Análogamente, para la masa 2

$\vec{F}_{n2} =\vec{F}_2=\left(-80\vec{\imath}+60\vec{\jmath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}^2}$

La resultante de estas fuerzas es su suma vectorial

$\vec{F}=\vec{F}_1+\vec{F}_2 = \left(-160\vec{\imath}\right)\frac{\mathrm{g}\cdot\mathrm{cm}}{\mathrm{s}^2}$

Esta resultante es igual a la masa total del sistema multiplicada por la la aceleración del CM.

El momento resultante respecto al punto O de las fuerzas ejercidas por el aro es la suma de los dos productos vectoriales

$\vec{M}_O = \vec{r}_1\times\vec{F}_1+\vec{r}_2\times\vec{F}_2$

Sin embargo, ambas fuerzas son paralelas a los respectivos vectores de posición, por lo que

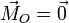
$\vec{M}_O = \vec{0}$

Para el momento respecto al CM aplicamos de nuevo la descomposición

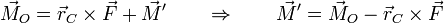
$\vec{M}_O = \vec{r}_C\times\vec{F}+\vec{M}'\qquad\Rightarrow\qquad \vec{M}'=\vec{M}_O-\vec{r}_C\times\vec{F}$

La resultante de las fuerzas también es paralela al vector de posición del CM, luego en estasustracción los dos términos son nulos y

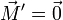
$\vec{M}'=\vec{0}$

A este resultado también se llega observando que puesto que la velocidad angular es constante

$\vec{M}_O = I_O\vec{\alpha}=\vec{0}\qquad\qquad \vec{M}'=I_C\vec{\alpha} = \vec{0}$

Dos masas unidas en un aro

De Laplace

Contenido

1 Enunciado

2 Posiciones, velocidades y aceleraciones

2.1 Posiciones

2.2 Velocidades

2.3 Aceleraciones

3 Velocidad angular

4 Momento cinético y energía cinética

4.1 Momento cinético

4.2 Energía cinética

5 Fuerzas y momentos

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES