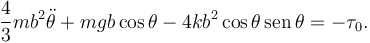De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

El sistema de la figura consta de dos barra articuladas. La longitud de las dos barras es $L = 2 b$ . La masa de la barra "2" es $m$ , mientras que la de la masa "0" es despreciable. Las barras se articulan entre sí en el punto $B$ . El extremo $A$ de la barra "0" se conecta con un pasador, de modo que desliza sobre el eje fijo $O X 1$ . La barra "2" está articulada sobre el eje $O X 1$ en el punto fijo $C$ . Un muelle de constante elástica $k$ y longitud natural nula conecta los centros de las barras.

Determina gráfica y analíticamente la posición de los CIR de los tres movimientos que se pueden definir en el sistema.
¿Cuántos grados de libertad tiene el problema?. Encuentra reducciones cinemáticas de los movimientos ${21}$ , ${20}$ y ${01}$ . Las reducciones deben expresarse en función de los grados de libertad.
Calcula la energía cinética y potencial del sistema.
Determina la posición de equilibrio.
Se aplica un par 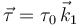$\vec{\tau}=\tau_0\,\vec{k}_1$ sobre la barra "2". Dibuja el diagrama de fuerzas y pares que actúan sobre cada barra.
Calcula la cantidad de movimiento de cada barra.
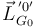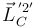Calcula $\vec{L}^{\,'0'}_{G_0}$ y $\vec{L}^{\,'2'}_C$ .
Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el sistema.
Escribe la función de Lagrange y las ecuaciones de Lagrange del sistema.

2 Solución

2.1 Posiciones de los C.I.R.s

Las barras están articuladas en el punto $B$ . Por tanto

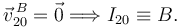
$\vec{v}^{\,B}_{20} = \vec{0} \Longrightarrow I_{20}\equiv B.$

La barra "2" esta articulada en el punto fijo $C$ . Entonces

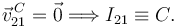
$\vec{v}^{\,C}_{21} = \vec{0} \Longrightarrow I_{21}\equiv C.$

El punto $A$ desliza sobre el eje fijo $O X 1$ . Entonces 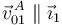$\vec{v}^{\,A}_{01}\parallel \vec{\imath}_1$ . El C.I.R. $I 01$ debe estar en la recta perpendicular a esta velocidad trazada en $A$ . Por otro lado, el Teorema de los Tres Centros nos dice que ese C.I.R. también debe encontrarse en la recta que une $I 21$ y $I 20$ . El punto de corte nos da la posición de $I 01$ . Los vectores de posición de estos puntos son

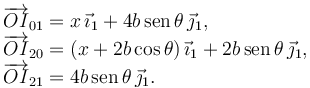
$\begin{array}{l} \overrightarrow{OI}_{01} = x\,\vec{\imath}_1 + 4b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1,\\ \overrightarrow{OI}_{20} = (x + 2b\cos\theta)\,\vec{\imath}_1 + 2b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1,\\ \overrightarrow{OI}_{21} = 4b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1. \end{array}$

2.2 Cinemática

Observando el dibujo tenemos

$\vec{\omega}_{01} = \dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,A}_{01} = \dot{x}\,\vec{\imath}_1.$

Para la barra "2" tenemos

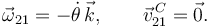
$\vec{\omega}_{21} = -\dot{\theta}\,\vec{k}, \qquad \vec{v}^{\,C}_{21} = \vec{0}.$

Ahora aplicamos el vínculo en el punto de articulación de las barras: 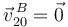$\vec{v}^{\,B}_{20}=\vec{0}$ . Usando las leyes de composición de velocidades

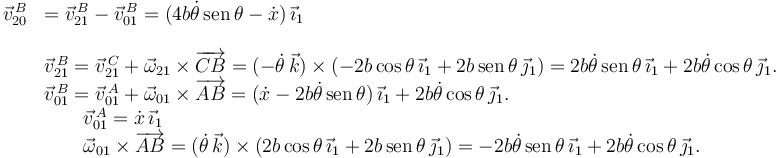
$\begin{array}{ll} \vec{v}^{\,B}_{20} &= \vec{v}^{\,B}_{21} - \vec{v}^{\,B}_{01}= (4b\dot{\theta}\,\mathrm{sen}\,\theta - \dot{x})\,\vec{\imath}_1 \\ &\\ & \vec{v}^{\,B}_{21} = \vec{v}^{\,C}_{21} + \vec{\omega}_{21}\times\overrightarrow{CB} = (-\dot{\theta}\,\vec{k})\times(-2b\cos\theta\,\vec{\imath}_1 + 2b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) = 2b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + 2b\dot{\theta}\cos\theta\,\vec{\jmath}_1.\\ & \vec{v}^{\,B}_{01} = \vec{v}^{\,A}_{01} + \vec{\omega}_{01}\times\overrightarrow{AB} = (\dot{x} -2b\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 + 2b\dot{\theta}\cos\theta\,\vec{\jmath}_1. \\ & \qquad \vec{v}^{\,A}_{01} = \dot{x}\,\vec{\imath}_1\\ & \qquad \vec{\omega}_{01}\times\overrightarrow{AB}= (\dot{\theta}\,\vec{k})\times(2b\cos\theta\,\vec{\imath}_1 + 2b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) = -2b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + 2b\dot{\theta}\cos\theta\,\vec{\jmath}_1. \end{array}$

Para que esa velocidad se anula debe cumplirse

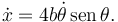
$\dot{x} = 4b\dot{\theta}\,\mathrm{sen}\,\theta.$

Otra forma de obtener esta expresión es darse cuenta de que

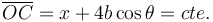
$\overline{OC} = x + 4b\cos\theta = cte.$

Derivando respecto al tiempo esta expresión se obtiene el resultado anterior.

Así pues, el sistema tiene un grado de libertad. Elegimos la coordenada ${θ}$ para trabajar. Las reducciones cinemáticas quedan

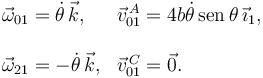
$\begin{array}{ll} \vec{\omega}_{01} = \dot{\theta}\,\vec{k}, & \vec{v}^{\,A}_{01} = 4b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1, \\ &\\ \vec{\omega}_{21} = -\dot{\theta}\,\vec{k}, & \vec{v}^{\,C}_{01} = \vec{0}. \end{array}$

2.3 Energía cinética y potencial

La masa de la barra "0" es despreciable. Por tanto, no contribuye ni a la energía cinética ni a la energía potencial del sistema.

La barra "2" tiene un punto fijo. Entonces su energía cinética puede expresarse

$T^{'2'} = \dfrac{1}{2}I_C|\vec{\omega}_{21}|^2 = \dfrac{2}{3}mb^2\dot{\theta}^2. \qquad\qquad (I_C = mL^2/3 = 4mb^2/3)$

Su energía potencial gravitatoria es

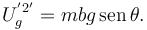
$U^{'2'}_g = mbg\,\mathrm{sen}\,\theta.$

La energía potencial elástica del muelle es

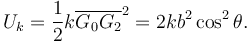
$U_k = \dfrac{1}{2}k\overline{G_0G_2}^2 = 2kb^2\cos^2\theta.$

Entonces, la energía potencial total es

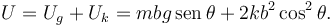
$U = U_g + U_k = mbg\,\mathrm{sen}\,\theta + 2kb^2\cos^2\theta.$

2.4 Posición de equilibrio

Como no hay fuerzas aplicadas no conservativas, la condición de equilibrio es

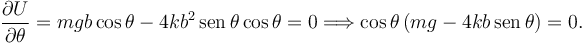
$\dfrac{\partial U}{\partial\theta} = mgb\cos\theta - 4kb^2\,\mathrm{sen}\,\theta\cos\theta = 0 \Longrightarrow \cos\theta\,(mg-4kb\,\mathrm{sen}\,\theta) = 0.$

Tenemos dos posibles soluciones

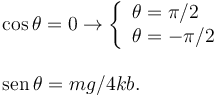
$\begin{array}{l} \cos\theta = 0 \to \left\{\begin{array}{l} \theta=\pi/2 \\ \theta=-\pi/2\end{array}\right.\\ \\ \mathrm{sen}\,\theta = mg/4kb. \end{array}$

La última posición sólo puede observarse si $m g < 4 k b$ , pues el seno debe ser siempre menor que 1.

Aunque no se pide en el enunciado, vamos a analizar la estabilidad de estas posiciones de equilibrio. Para ello calculamos la derivada segunda del potencial

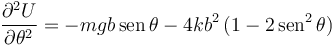
$\dfrac{\partial^2U}{\partial\theta^2} = -mgb\,\mathrm{sen}\,\theta - 4kb^2\,(1-2\,\mathrm{sen}^2\,\theta)$

Ahora evaluamos la segunda derivada en las posiciones de equilibrio

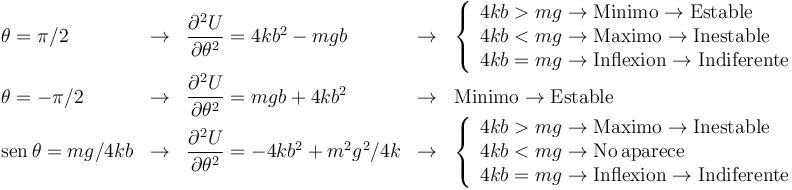
$\begin{array}{lclcl} \theta = \pi/2 & \to & \dfrac{\partial^2U}{\partial\theta^2} = 4kb^2-mgb &\to &\left\{ \begin{array}{l} 4kb>mg \to \mathrm{Minimo} \to \mathrm{Estable}\\ 4kb<mg \to \mathrm{Maximo} \to \mathrm{Inestable}\\ 4kb=mg \to \mathrm{Inflexion} \to \mathrm{Indiferente} \end{array} \right. \\ \theta = -\pi/2 & \to & \dfrac{\partial^2U}{\partial\theta^2} = mgb + 4kb^2&\to & \mathrm{Minimo} \to \mathrm{Estable}\\ \mathrm{sen}\,\theta = mg/4kb & \to & \dfrac{\partial^2U}{\partial\theta^2} = -4kb^2+ m^2g^2/4k &\to &\left\{ \begin{array}{l} 4kb>mg \to \mathrm{Maximo} \to \mathrm{Inestable}\\ 4kb<mg \to \mathrm{No\, aparece}\\ 4kb=mg \to \mathrm{Inflexion} \to \mathrm{Indiferente} \end{array} \right. \end{array}$

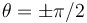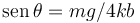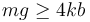La gráfica representa la función $U / k b 2$ en función del ángulo. Vemos que cuando $m g < 4 k b$ la función tiene dos mínimos y un máximo. Los mínimos son las soluciones estables ( $\theta=\pm\pi/2$ ) y el máximo la inestable ( $\mathrm{sen}\,\theta=mg/4kb$ ). Cuando $mg\geq4kb$ sólo hay un mínimo ( $θ = - π / 2$ ). En el caso $m g = 4 k b$ la curva es plana en $θ = π / 2$ correspondiendo a la situación de equilibrio indiferente.

2.5 Diagrama de fuerzas con par aplicado

La figura de la derecha muestra las fuerzas y pares que actúan sobre cada sólido. Sus expresiones en la base "1" son

Sólido 2

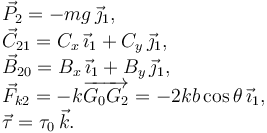
$\begin{array}{l} \vec{P}_2 = -mg\,\vec{\jmath}_1,\\ \vec{C}_{21} = C_x\,\vec{\imath}_1 + C_y\,\vec{\jmath}_1,\\ \vec{B}_{20} = B_x\,\vec{\imath}_1 + B_y\,\vec{\jmath}_1,\\ \vec{F}_{k2} = -k\overrightarrow{G_0G_2} = -2kb\cos\theta\,\vec{\imath}_1,\\ \vec{\tau} = \tau_0\,\vec{k}. \end{array}$

Sólido 0

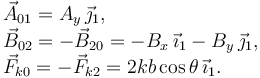
$\begin{array}{l} \vec{A}_{01} = A_y\,\vec{\jmath}_1,\\ \vec{B}_{02} = -\vec{B}_{20} = -B_x\,\vec{\imath}_1 - B_y\,\vec{\jmath}_1,\\ \vec{F}_{k0} = -\vec{F}_{k2} = 2kb\cos\theta\,\vec{\imath}_1.\\ \end{array}$

Las incógnitas del problema son: ${θ, C x, C y, B x, B y, A y}$ . Son 6, por lo que el problema puede resolverse aplicando los teoremas fundamentales.

2.6 Cantidad de movimiento y momentos angulares

La barra "0" no tiene ni cantidad de movimiento ni momento angular, pues no tiene masa. Para la barra "2" la cantidad de movimiento es

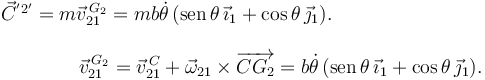
$\begin{array}{l} \vec{C}^{'2'} = m\vec{v}^{\,G_2}_{21} = mb\dot{\theta}\,(\mathrm{sen}\,\theta\,\vec{\imath}_1 + \cos\theta\,\vec{\jmath}_1). \\ \\ \qquad\qquad\vec{v}^{\,G_2}_{21} = \vec{v}^{\,C}_{21} + \vec{\omega}_{21}\times\overrightarrow{CG_2} = b\dot{\theta}\,(\mathrm{sen}\,\theta\,\vec{\imath}_1 + \cos\theta\,\vec{\jmath}_1). \end{array}$

Para calcular el momento angular pedido aprovechamos que $C$ es un punto fijo

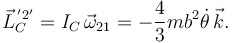
$\vec{L}^{\,'2'}_C = I_C\,\vec{\omega}_{21} = -\dfrac{4}{3}mb^2\dot{\theta}\,\vec{k}.$

2.7 Ecuaciones aplicando los teoremas fundamentales

2.7.1 T.C.M.

Sólido 2 Tenemos

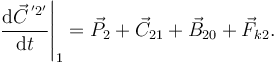
$\left.\dfrac{\mathrm{d}\vec{C}^{\,'2'}}{\mathrm{d}t}\right|_1 = \vec{P}_2 + \vec{C}_{21} + \vec{B}_{20} + \vec{F}_{k2}.$

La derivada temporal es

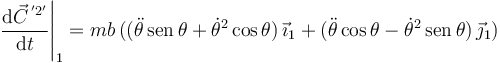
$\left.\dfrac{\mathrm{d}\vec{C}^{\,'2'}}{\mathrm{d}t}\right|_1 = mb\,((\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta)\,\vec{\imath}_1 + (\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1)$

Obtenemos así dos ecuaciones

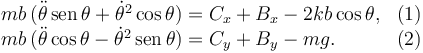
$\begin{array}{lr} mb\,(\ddot{\theta}\,\mathrm{sen}\,\theta + \dot{\theta}^2\cos\theta) = C_x + B_x - 2kb\cos\theta, & (1)\\ mb\,(\ddot{\theta}\cos\theta - \dot{\theta}^2\,\mathrm{sen}\,\theta) = C_y + B_y -mg. & (2) \end{array}$

Sólido 2 En este caso la derivada temporal se anula pues la cantidad de movimiento es cero

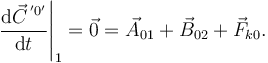
$\left.\dfrac{\mathrm{d}\vec{C}^{\,'0'}}{\mathrm{d}t}\right|_1 = \vec{0}= \vec{A}_{01} + \vec{B}_{02} + \vec{F}_{k0}.$

Obtenemos así dos ecuaciones

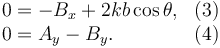
$\begin{array}{lr} 0 = -B_x + 2kb\cos\theta, & (3)\\ 0 = A_y - B_y. & (4) \end{array}$

2.7.2 T.M.C.

Sólido 2 Como el punto $C$ es fijo, aplicamos el T.M.C. en él

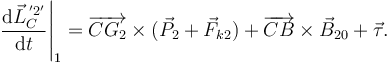
$\left.\dfrac{\mathrm{d}\vec{L}^{\,'2'}_C}{\mathrm{d}t}\right|_1 = \overrightarrow{CG_2}\times(\vec{P}_2 + \vec{F}_{k2}) + \overrightarrow{CB}\times\vec{B}_{20} + \vec{\tau}.$

El peso y la fuerza elástica están aplicados en el mismo punto y el par externo está aplicado en el sólido "2".

La derivada temporal es

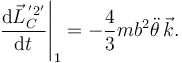
$\left.\dfrac{\mathrm{d}\vec{L}^{\,'2'}_{C}}{\mathrm{d}t}\right|_1 = -\dfrac{4}{3}mb^2\ddot{\theta}\,\vec{k}.$

Haciendo los productos vectoriales (sabiendo que 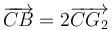$\overrightarrow{CB} = 2\overrightarrow{CG_2}$ obtenemos otra ecuación

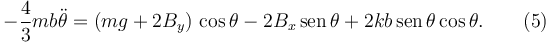
$-\dfrac{4}{3}mb\ddot{\theta} = (mg+ 2B_y)\,\cos\theta - 2B_x\,\mathrm{sen}\,\theta + 2kb\,\mathrm{sen}\,\theta\cos\theta. \qquad (5)$

Sólido 0 De nuevo, la derivada temporal es nula porque el momento angular es nulo. Aplicando el T.M.C. en el centro de masas tenemos

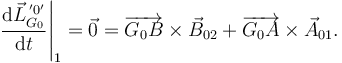
$\left.\dfrac{\mathrm{d}\vec{L}^{\,'0'}_{G_0}}{\mathrm{d}t}\right|_1 = \vec{0} = \overrightarrow{G_0B}\times\vec{B}_{02} + \overrightarrow{G_0A}\times\vec{A}_{01}.$

Haciendo los productos vectoriales obtenemos la última ecuación

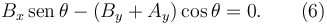
$B_x\,\mathrm{sen}\,\theta - (B_y+A_y)\cos\theta = 0. \qquad (6)$

2.8 Ecuaciones de Lagrange

La función de Lagrange es

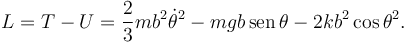
$L = T - U = \dfrac{2}{3}mb^2\dot{\theta}^2 - mgb\,\mathrm{sen}\,\theta - 2kb^2\cos\theta^2.$

Hay sólo una ecuación de Lagrange, pues hay sólo un grado de libertad. Hay que tener en cuenta que hay un par aplicado que no está incluido en la Lagrangiana. Por tanto, la ecuación es

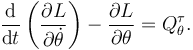
$\dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right) - \dfrac{\partial L}{\partial\theta} = Q^{\tau}_{\theta}.$

Calculamos los diferentes términos

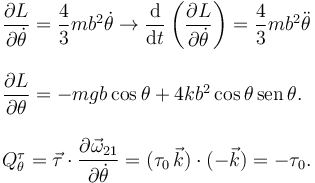
$\begin{array}{l} \dfrac{\partial L}{\partial\dot{\theta}} = \dfrac{4}{3}mb^2\dot{\theta} \to \dfrac{\mathrm{d}}{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right) = \dfrac{4}{3}mb^2\ddot{\theta}\\ \\ \dfrac{\partial L}{\partial\theta} = -mgb\cos\theta + 4kb^2\cos\theta\,\mathrm{sen}\,\theta.\\ \\ Q^{\tau}_{\theta} = \vec{\tau}\cdot\dfrac{\partial\vec{\omega}_{21}}{\partial\dot{\theta}} = (\tau_0\,\vec{k})\cdot(-\vec{k}) = -\tau_0. \end{array}$

Finalmente, la ecuación de Lagrange es

$\dfrac{4}{3}mb^2\ddot{\theta} + mgb\cos\theta - 4kb^2\cos\theta\,\mathrm{sen}\,\theta = -\tau_0.$

Dos barras articuladas con muelle (Feb. 2020)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Posiciones de los C.I.R.s

2.2 Cinemática

2.3 Energía cinética y potencial

2.4 Posición de equilibrio

2.5 Diagrama de fuerzas con par aplicado

2.6 Cantidad de movimiento y momentos angulares

2.7 Ecuaciones aplicando los teoremas fundamentales

2.7.1 T.C.M.

2.7.2 T.M.C.

2.8 Ecuaciones de Lagrange

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES