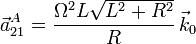Disco y varilla con movimiento conico
De Laplace
Contenido |
1 Enunciado
(Final, Diciembre 2009, P1)
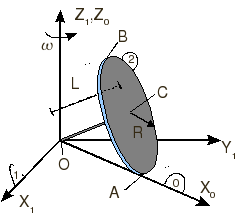
A un disco de radio R y espesor despreciable se le acopla en su centro una barra
perpendicular a él (sólido "2") de longitud L. El disco gira de modo que el extremo de esta barra permanece fijo en el
punto O1, como se indica en la figura, y rueda sin deslizar sobre el plano OX1Y1. El eje
X0 (sólido "0") se elige de modo que acompaña al disco en su giro. La velocidad angular
es 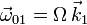 con Ω constante.
con Ω constante.
- Aplicando las leyes de composición de movimientos, calcula la velocidad angular
 y la aceleración angular
y la aceleración angular 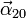 .
.
- Determina las reducciones cinemáticas de los movimientos {01}, {20} y {21}, así como las ecuaciones vectoriales de los respectivos ejes de rotación y mínimo deslizamiento.
- Calcula
 y
y 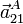 en el instante indicado en la figura.
en el instante indicado en la figura.
- Calcula numéricamente los vectores de los apartados 1 y 3 si se tiene L=4 cm, R=3 cm, ω=5 s-1.
2 Solución
Vamos a analizar los movimientos {01} y {21}, y a partir de su composición obtendremos las magnitudes del movimiento {20}.
2.1 Movimiento {01}
Esta es una rotación pura, con eje de giro permanente que coincide con la línea
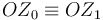 . La velocidad angular es la dada en el enunciado y
es constante en el tiempo. Podemos reducir en el punto O, que al
estar siempre en el eje tiene velocidad nula siempre. La reducción cinemática de
este movimiento es
. La velocidad angular es la dada en el enunciado y
es constante en el tiempo. Podemos reducir en el punto O, que al
estar siempre en el eje tiene velocidad nula siempre. La reducción cinemática de
este movimiento es

La ecuación vectorial del eje de rotación es
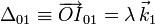
Podemos también calcular las aceleraciones angular y lineal en el punto O

2.2 Movimiento {21}
El enunciado nos dice que el disco rueda sin deslizar, por tanto
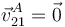 . Por otro lado el punto O
pertenece tanto a la varilla (sólido "2") como al eje OX1 (sólido
"1"). Entonces también tenemos
. Por otro lado el punto O
pertenece tanto a la varilla (sólido "2") como al eje OX1 (sólido
"1"). Entonces también tenemos 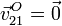 . Como la
velocidad es nula en los puntos O y A, el eje de
rotación Δ21 debe pasar por esos puntos. Entonces la
velocidad angular
. Como la
velocidad es nula en los puntos O y A, el eje de
rotación Δ21 debe pasar por esos puntos. Entonces la
velocidad angular  es de la forma
es de la forma
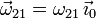
Necesitamos la velocidad en otro punto para poder determinar ω21. Para ello nos fijamos en el puntp C. Este punto pertenece
a la vez al sólido "2" (el disco) y al sólido "0" (el plano OX0Z0. Esto quiere decir que 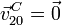 . Utilizando
la descomposición {21}={20}+{01} tenemos
. Utilizando
la descomposición {21}={20}+{01} tenemos
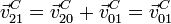
Pero esta velocidad la podemos calcular a partir de la reducción del movimiento {01}. Tenemos
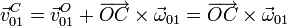
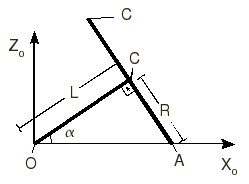
Para obtener el vector  observamos la figura de
la derecha. Tenemos
observamos la figura de
la derecha. Tenemos
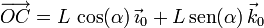
y para el ángulo α se tiene

Es decir
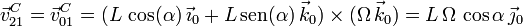
Ahora podemos calcular ω21 utilizando la ecuación del campo de velocidades del movimiento {21} para relacionar las velocidades en los puntos O y C
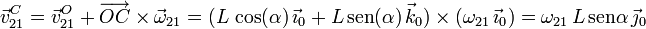
Comparando esta expresión con la que hemos obtenido antes para
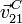 obtenemos
obtenemos
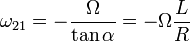
La reducción cinemática del movimiento {21} en el punto O es
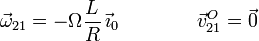
La ecuación vectorial del eje instantáneo de rotación Δ21 es
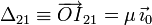
Para calcular la aceleración angular hay que utilizar la ecuación de Poisson que relaciona la derivada temporal en el triedro "0" con la derivada en en el triedro "1"
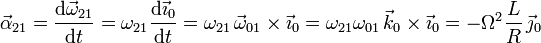
Y teniendo en cuenta que el punto O pertenece en todo instante tanto al sólido "2" como al "1", se tiene
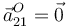
2.3 Movimiento {20}
Para caracterizar este movimiento utilizamos la composición
{21} = {20} + {01}
Tenemos
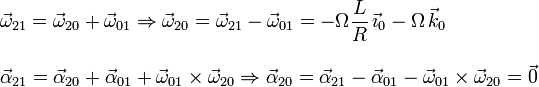
Calculamos la velocidad y aceleración en el punto O usando la misma composición
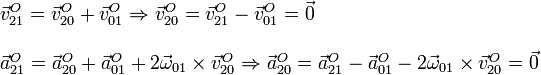
El punto O pertenece al eje instantáneo de rotación Δ20. Su ecuación vectorial es
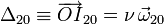
2.4 Cálculo de vB21
Calculamos  a partir de la reducción del movimiento
{21} en el punto O. Utilizando la ecuación del campo de
velocidades de este movimiento tenemos
a partir de la reducción del movimiento
{21} en el punto O. Utilizando la ecuación del campo de
velocidades de este movimiento tenemos
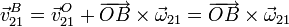
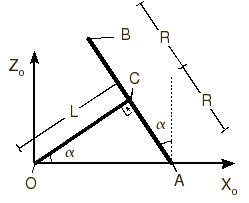
El vector 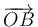 se puede expresar como
se puede expresar como
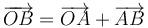
De la figura tenemos
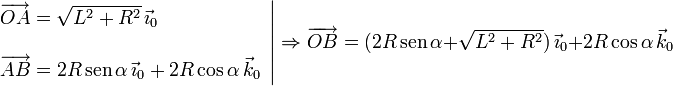
La velocidad buscada es
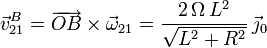
2.5 Cálculo de aA21
Ahora utilizamos la ecuación del campo de aceleraciones del movimiento {21}. Partiendo del punto O tenemos
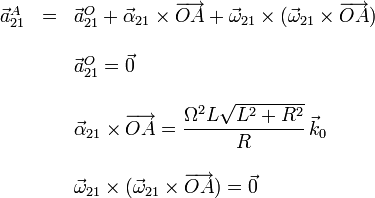
Por tanto