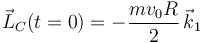Disco con barra articulada, Noviembre 2015 (MR G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

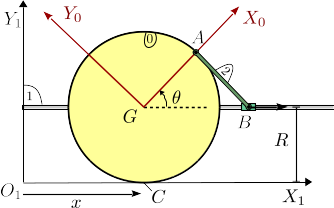
El disco de la figura (sólido "0"), de masa $m$ y radio $R$ , rueda sin deslizar sobre el eje $O X 1$ . Una barra (sólido "2"), de masa $m$ y longitud $R$ , se encuentra articulada en el punto $A$ de la circunferencia del disco. El otro extremo, $B$ se conecta a un deslizador que se mueve sobre una barra paralela al eje $O X 1$ . En el instante inicial los puntos $G$ y $A$ se encontraban sobre el eje $O 1 Y 1$ (con el punto $A$ por encima del $G$ ).

Calcula la velocidad absoluta del punto $A$ .
Determina la velocidad de rotación $\vec{\omega}_{20}$ .
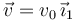En esta pregunta y las siguientes suponemos que el punto $B$ se mueve con velocidad $\vec{v}=v_0\,\vec{\imath}_1$ . Calcula el valor de $\dot{\theta}$ .
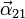Calcula el valor de $\vec{\alpha}_{21}$ .
Determina el valor de 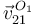$\vec{v}^{\,O_1}_{21}$ en el instante incial.
Calcula el momento cinético del disco respecto al punto de contacto con el suelo en el instante inicial.

2 Solución

2.1 Velocidad absoluta del punto $A$

Se trata de un movimiento plano. En este caso podemos encontrar una expresión que nos da el vector de posición del punto $A$ válida para todo instante de tiempo. Tenemos

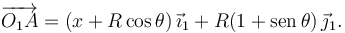
$\overrightarrow{O_1A} = (x+R\cos\theta)\,\vec{\imath}_1 + R(1+\mathrm{sen}\,\theta)\,\vec{\jmath}_1.$

La velocidad absoluta del punto $A$ es

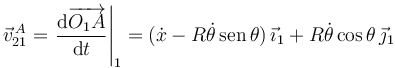
$\vec{v}^{\,A}_{21} = \left.\dfrac{\mathrm{d}\overrightarrow{O_1A}}{\mathrm{d}t}\right|_1= (\dot{x} - R\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 + R\dot{\theta}\cos\theta\,\vec{\jmath}_1$

Existe un vínculo interligado entre $x$ y $θ$ . Para explicitarlo usamos la reducción cinemática del movimiento {01}.

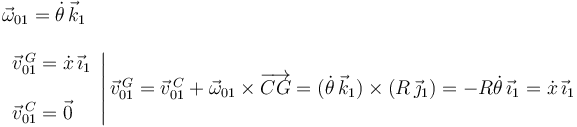
$\begin{array}{l} \vec{\omega}_{01} = \dot{\theta}\,\vec{k}_1 \\ \\ \left. \begin{array}{l} \vec{v}^{\,G}_{01} = \dot{x}\,\vec{\imath}_1\\ \\ \vec{v}^{\,C}_{01} = \vec{0} \end{array}\right| \vec{v}^{\,G}_{01} = \vec{v}^{\,C}_{01} + \vec{\omega}_{01}\times\overrightarrow{CG} =(\dot{\theta}\,\vec{k}_1)\times(R\,\vec{\jmath}_1) = -R\dot{\theta}\,\vec{\imath}_1 =\dot{x}\,\vec{\imath}_1 \end{array}$

Por tanto tenemos 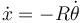$\dot{x} = -R\dot{\theta}$ y la velocidad pedida es

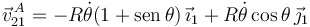
$\vec{v}^{\,A}_{21} = -R\dot{\theta}(1+\mathrm{sen}\,\theta)\,\vec{\imath}_1 +R\dot{\theta}\cos\theta\,\vec{\jmath}_1$

2.2 Velocidad de rotación del punto $B$

La forma mas fácil de calcular este valor es darse cuenta, observando la figura, de que la barra (y por tanto un uje $X 2$ que coincida con ella) forma un ángulo $θ$ con el eje $X 1$ , pues el triángulo $G A B$ es isósceles. La rotación del movimiento {21} es

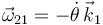
$\vec{\omega}_{21} = -\dot{\theta}\,\vec{k}_1$

Usando las leyes de composición {21} = {20} + {01}

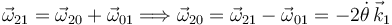
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = -2\dot\theta\,\vec{k}_1$

2.3 Valor de $\dot{\theta}$

El vector absoluto de posición del punto $B$ es

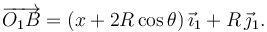
$\overrightarrow{O_1B} = (x+2R\cos\theta)\,\vec{\imath}_1 + R\,\vec{\jmath}_1.$

La velocidad absoluta del punto $B$ es

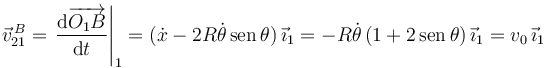
$\vec{v}^{\,B}_{21} = \left.\dfrac{\mathrm{d}\overrightarrow{O_1B}}{\mathrm{d}t}\right|_1= (\dot{x} - 2R\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 = -R\dot{\theta}\,(1+ 2\,\mathrm{sen}\,\theta)\,\vec{\imath}_1 = v_0\,\vec{\imath}_1$

Por tanto

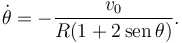
$\dot{\theta} = -\dfrac{v_0}{R(1+2\,\mathrm{sen}\,\theta)}.$

2.4 Aceleración angular 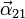$\vec{\alpha}_{21}$

Hemos visto antes que

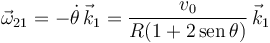
$\vec{\omega}_{21} = -\dot{\theta}\,\vec{k}_1 = \dfrac{v_0}{R(1+2\,\mathrm{sen}\,\theta)}\,\vec{k}_1$

Derivamos respecto del tiempo

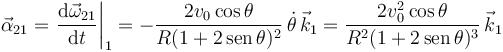
$\vec{\alpha}_{21} = \left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1 = -\dfrac{2v_0\cos\theta}{R(1+2\,\mathrm{sen}\,\theta)^2}\,\dot{\theta}\,\vec{k}_1 = \dfrac{2v_0^2\cos\theta}{R^2(1+2\,\mathrm{sen}\,\theta)^3}\,\vec{k}_1$

2.5 Velocidad 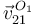$\vec{v}^{\,O_1}_{21}$ en el instante inicial

En el instante inicial tenemos $θ = π / 2$ , pues el punto $A$ esta en el eje $O 1 Y 1$ encima del punto $G$ . Entonces

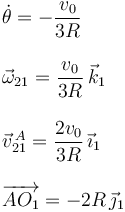
$\begin{array}{l} \dot{\theta} = -\dfrac{v_0}{3R}\\ \\ \vec{\omega}_{21} = \dfrac{v_0}{3R}\,\vec{k}_1\\ \\ \vec{v}^{\,A}_{21} = \dfrac{2v_0}{3R}\,\vec{\imath}_1\\ \\ \overrightarrow{AO_1} = -2R\,\vec{\jmath}_1 \end{array}$

Usando el Teorema de Chasles para el movimiento {21} tenemos

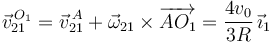
$\vec{v}^{\,O_1}_{21} = \vec{v}^{\,A}_{21} + \vec{\omega}_{21} \times\overrightarrow{AO_1} = \dfrac{4v_0}{3R}\,\vec{\imath}_1$

Esta velocidad no es cero. En ese instante hay tres puntos distintos en el punto geométrico $O 1$ , uno por cada sólido que consideramos. Sólo los puntos que pertenecen a los sólidos "0" y "1" tienen velocidad cero respecto al sólido "1".

2.6 Momento cinético 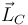$\vec{L}_C$ en el instante inicial

Al ser un movimiento plano, el eje $Z 1$ es eje principal de inercia en todos los puntos de los sólidos. Por tanto

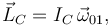
$\vec{L}_C = I_C\,\vec{\omega}_{01},$

donde $I C$ es el momento de inercia del disco respecto a un eje perpendicular a él que pase por $C$ . Usando el teorema de Steiner o de los ejes paralelos, lo relacionamos con el momento de inercia respecto al centro de masas

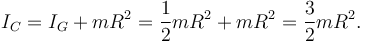
$I_C = I_G + mR^2 = \dfrac{1}{2}mR^2 + mR^2 = \dfrac{3}{2}mR^2.$

En el instante inicial

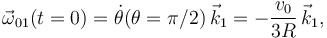
$\vec{\omega}_{01}(t=0) = \dot{\theta}(\theta=\pi/2)\,\vec{k}_1 = -\dfrac{v_0}{3R}\,\vec{k}_1,$

y por tanto

$\vec{L}_C(t=0) = -\dfrac{mv_0R}{2}\,\vec{k}_1$

Disco con barra articulada, Noviembre 2015 (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad absoluta del punto $A$

2.2 Velocidad de rotación del punto $B$

2.3 Valor de $\dot{\theta}$

2.4 Aceleración angular $\vec{\alpha}_{21}$

2.5 Velocidad $\vec{v}^{\,O_1}_{21}$ en el instante inicial

2.6 Momento cinético $\vec{L}_C$ en el instante inicial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Disco con barra articulada, Noviembre 2015 (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Velocidad absoluta del punto A

2.2 Velocidad de rotación del punto B

2.3 Valor de

2.4 Aceleración angular

2.5 Velocidad en el instante inicial

2.6 Momento cinético en el instante inicial

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1 Velocidad absoluta del punto $A$

2.2 Velocidad de rotación del punto $B$

2.3 Valor de $\dot{\theta}$

2.4 Aceleración angular $\vec{\alpha}_{21}$

2.5 Velocidad $\vec{v}^{\,O_1}_{21}$ en el instante inicial

2.6 Momento cinético $\vec{L}_C$ en el instante inicial