Disco cayendo Segunda Prueba de Control (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un disco de radio $R$ cae en dirección vertical rodando sin deslizar sobre una cuerda vertical. El módulo de la velocidad del centro del disco es 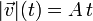$|\vec{v}|(t) = A\,t$ , siendo $A$ una constante. Calcula

Velocidad angular del movimiento {21}.
La velocidad $\vec{v}_{21}^B$ .
La acelaración $\vec{a}_{21}^B$ .

2 Solución

2.1 Velocidad angular

El vector rotación angular es perpendicular al plano del dibujo. Por tanto

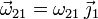
$\vec{\omega}_{21} = \omega_{21}\,\vec{\jmath}_1$

Como el disco rueda sin deslizar sobre el hilo en el punto $A$ tenemos

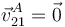
$\vec{v}_{21}^A = \vec{0}$

Además, siguiendo el enunciado la velocidad del punto $C$ es

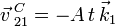
$\vec{v}\,^C_{21} = -A\,t\,\vec{k}_1$

Usando la ecuación del campo de velocidades

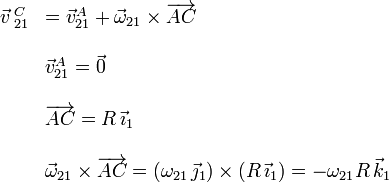
$\begin{array}{rl} \vec{v}\,^C_{21} &= \vec{v}_{21}^A + \vec{\omega}_{21}\times\overrightarrow{AC} \\&\\ &\vec{v}_{21}^A = \vec{0} \\&\\ &\overrightarrow{AC} = R\,\vec{\imath}_1 \\&\\ &\vec{\omega}_{21}\times\overrightarrow{AC} = (\omega_{21}\,\vec{\jmath}_1)\times(R\,\vec{\imath}_1) =-\omega_{21}R\,\vec{k}_1 \end{array}$

Comparando con la expresión anterior de 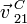$\vec{v}\,^C_{21}$ tenemos

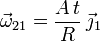
$\vec{\omega}_{21} = \dfrac{A\,t}{R}\,\vec{\jmath}_1$

2.2 Velocidad del punto B

Utilizamos de nuevo la ecuación del campo de velocidades

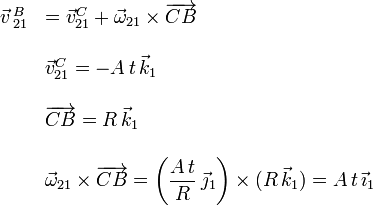
$\begin{array}{rl} \vec{v}\,^B_{21} &= \vec{v}_{21}^C + \vec{\omega}_{21}\times\overrightarrow{CB} \\&\\ &\vec{v}_{21}^C = -A\,t\,\vec{k}_1 \\&\\ &\overrightarrow{CB} = R\,\vec{k}_1 \\&\\ &\vec{\omega}_{21}\times\overrightarrow{CB} = \left(\dfrac{A\,t}{R}\,\vec{\jmath}_1\right)\times(R\,\vec{k}_1) = A\,t\,\vec{\imath}_1 \end{array}$

El resultado final es

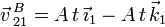
$\vec{v}\,^B_{21} = A\,t\,\vec{\imath}_1 -A\,t\,\vec{k}_1$

2.3 Aceleración del punto B

La velocidad del punto $C$ obtenida en el apartado anterior es válida para todo instante de tiempo. Entonces

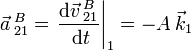
$\vec{a}\,^B_{21} = \left.\dfrac{\mathrm{d}\vec{v}\,^B_{21}}{\,\mathrm{d}t}\right|_1 = -A\,\vec{k}_1$

Obtenemos la aceleración angular derivando la velocidad angular

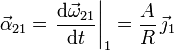
$\vec{\alpha}_{21} = \left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1 = \dfrac{A}{R}\,\vec{\jmath}_1$

Podemos calcular la aceleración del punto $B$ usando la ecuación del campo de aceleraciones

$\begin{array}{rl} \vec{a}\,^B_{21} &= \vec{a}_{21}^C + \vec{\alpha}_{21}\times\overrightarrow{CB} + \vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{CB}) \\&\\ &\vec{a}_{21}^C = -A\,\vec{k}_1 \\&\\ &\vec{\alpha}_{21}\times\overrightarrow{CB} =\left(\dfrac{A}{R}\,\vec{\jmath}_1\right)\times(R\,\vec{k}_1) = A\,\vec{\imath}_1 \\&\\ &\vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{CB)} = -\dfrac{A^2\,t^2}{R}\,\vec{k}_1 \end{array}$