Dimensiones y unidades (GIOI)

De Laplace

Contenido

1 Dimensiones
2 Unidades de medida

1 Dimensiones

1.1 Medidas directas e indirectas

En su versión más simple, una medida es la comparación de un resultado experimental con un patrón (unidad de medida). Esto es, cuando se dice que una distancia mide 3 m lo que se está diciendo es que la longitud medida es 3 veces la de la medida patrón, tomada como 1 m.

A partir de una serie de medidas experimentales directas pueden obtenerse cantidades indirectas o derivadas. Por ejemplo, para medir el área del suelo de una habitación rectangular nos basta con medir las longitudes de dos lados y aplicar la fórmula $S = b h$ . La existencia de estas relaciones permite definir las magnitudes en fundamentales y derivadas.

1.2 Dimensiones de una magnitud

Independientemente de la unidad que se emplee para expresar una magnitud física, estas se clasifican en tipos diferentes, según en la forma que puedan sumarse. Por ejemplo, podemos sumar una distancia de 3 km con una de 2 millas, o podemos sumar 5 kg a 3 libras, pero sabemos que es erróneo sumar 3 km con 5 kg. Vemos que hay algo más básico que la unidad de medida y es el tipo de magnitud de que se trata: distancia, masa, tiempo,… A cada uno de estos tipos se denomina dimensión y decimos que una magnitud tiene “dimensiones de distancia” o “dimensiones de masa”.

1.3 Homogeneidad dimensional

Para clasificar las magnitudes tenemos el principio de homogeneidad dimensional que establece que:

En toda ecuación y en toda suma, los términos igualados o sumados deben tener las mismas dimensiones.

Ésta es una forma elegante de decir “no se pueden sumar peras con manzanas”. Este principio constituye una herramienta extremadamente útil para detectar errores en los cálculos. Imaginemos que como resultado de un problema se llega a que una fuerza es igual a

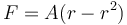
$F = A(r-r^2)\,$

siendo $r$ un radio y $A$ una constante. Esta ecuación es necesariamente incorrecta, sin necesidad de sustituir valor numérico alguno. Estamos sumando una distancia, $r$ , (que tiene dimensiones de longitud) con una distancia al cuadrado (que sería un área). Puesto que estas cantidades poseen dimensiones diferentes, la ecuación no es válida.

Aquí tenemos otro ejemplo de ecuación dimensionalmente incorrecta:

La homogeneidad dimensional permite localizar de forma rápida errores en los resultados de un problema.

Una relación entre magnitudes no implica ninguna unidad en concreto (solo las dimensiones). Al decir que la distancia Sevilla y Cádiz es la misma que entre Sevilla y Huelva, da igual que la midamos en kilómetros o en pulgadas. Por ello, es incorrecto escribir una ley como

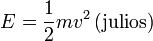$E = \frac{1}{2}mv^2\,(\mathrm{julios})$ (expresión incorrecta)

ya que la energía podría estar expresada en ergios, calorías, kilovatios·hora o muchas otras, dependiendo de en qué midamos la masa o la velocidad. Por ello, la regla es que si una fórmula es puramente algebraica, no hay que incluir las unidades. Por contra, si se sustituyen uno o todos los valores numéricos, es obligatorio incluir las unidades.

1.4 Ecuaciones dimensionales

Aunque magnitudes diferentes no se pueden sumar, si se pueden multiplicar. Podemos dividir una magnitud con dimensiones de distancia por una con dimensiones de tiempo y obtenemos una magnitud con dimensiones de velocidad. Escribimos esta relación

$[v] = \frac{[x]}{[t]}$

donde el corchete representa “dimensiones”. Debemos insistir en que esta ecuación no nos dice que la velocidad sea igual al espacio partido por el tiempo, sino que sus unidades son las de una distancia dividida por un tiempo (que pueden ser m/s o km/h, por ejemplo).

La homogeneidad dimensional nos permite determinar las dimensiones de cantidades desconocidas. Así, en la ley de Hooke

$F = -kx\,$

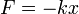
nos dice que la constante $k$ tiene dimensiones de fuerza partida por distancia

$[k]=\frac{[F]}{[x]}$

(por ejemplo, se medirá en N/m).

La existencia de relaciones entre dimensiones permite dividir las magnitudes en fundamentales y derivadas. De una relación como

$S = b\cdot h\,$

obtenemos que las dimensiones de área son las de una distancia al cuadrado, lo que podemos escribir como

$[b] = L\qquad\qquad [h] = L\qquad\Rightarrow\qquad [S] = L^2$

De esta forma, las dimensiones de cualquier magnitud se puede expresar como potencias de una serie de magnitudes fundamentales.

Así, por ejemplo, la velocidad equivale al cociente de una distancia dividida por un intervalo de tiempo y por tanto se verifica la ecuación dimensional

$[v] = \frac{[x]}{[t]} = L T^{-1}$

Aquí la distancia y el tiempo son consideradas magnitudes fundamentales y la velocidad una magnitud derivada.

Las magnitudes que se eligen como fundamentales e incluso el número de ellas es arbitrario. En el SI existen siete magnitudes fundamentales: longitud, tiempo, masa, intensidad de corriente eléctrica, cantidad de materia, temperatura termodinámica e intensidad luminosa. Todas las demás son derivadas.

Cada magnitud derivada posee una única ecuación dimensional, caracterizada por los diferentes exponentes de las magnitudes fundamentales.

Magnitud	Relación	Dimensiones
Área	$[S] = [x] 2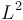$	$L^2\,$
Volumen	$[V] = [x] 3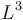$	$L^3\,$
Velocidad	$[v] = [x] / [t]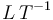$	$L\,T^{-1}\,$
Aceleración	$[a] = [v] / [t]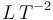$	$L\,T^{-2}\,$
Fuerza	$[F] = [m][a]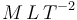$	$M\,L\,T^{-2}\,$
Trabajo	$[W] = [F][x]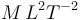$	$M\,L^2T^{-2}\,$
Potencia	$[P] = [W] / [t]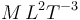$	$M\,L^2T^{-3}\,$

Teniendo las ecuaciones dimensionales de las diferentes magnitudes que aparecen en una ecuación, podemos establecer de forma sistemática si es dimensionalmente correcta.

Así, por ejemplo, la ecuación para una velocidad de impacto con el suelo

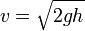
$v = \sqrt{2gh}$

con $h$ la altura inicial, $v$ la velocidad de impacto y $g$ la aceleración de la gravedad, cumple

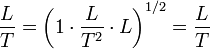
$\frac{L}{T} = \left(1\cdot\frac{L}{T^2}\cdot L\right)^{1/2} = \frac{L}{T}$

y por tanto es dimensionalmente correcta.

Hay que repetir que la homogeneidad es independiente de las unidades que se empleen para medir las cantidades. Por lo que sabemos, $h$ podría estar medido en leguas, y $v$ en micras/semana. Las dimensiones de una magnitud son algo más básico que las unidades en que se midan.

2 Unidades de medida

Las unidades de medida son arbitrarias y, en muchas ocasiones, se definen unidades específicas para un problema concreto. Por ejemplo, cuando se dice que un accidente ocurrió a medio camino entre Sevilla y Madrid, se está tomando como unidad de medida la distancia Sevilla-Madrid y se está diciendo que el accidente ocurrió en $x = 0.5 u$ .

Para poder hacer los resultados fácilmente interpretables y trasladables a otras situaciones, es preferible emplear un sistema de unidades estandarizado. De entre los diferentes sistemas de unidades en uso, el más aceptado y preceptivo legalmente en España, es el Sistema Internacional de Unidades (SI), que ha evolucionado desde el sistema métrico decimal elaborado durante la Revolución Francesa.

2.1 Homogeneidad en las unidades

En una fórmula que relaciona valores de diferentes magnitudes, cuando los valores de éstas se sustituyen, incluyendo sus unidades, también debe cumplirse la homogeneidad entre las unidades, esto es, que el primer miembro debe medirse en las mismas unidades que el segundo. Por ejemplo, supongamos que en la ecuación anterior 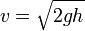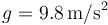$v = \sqrt{2gh}$ , $g = 9.8\,\mathrm{m}/\mathrm{s}^2$ ; y $h = 10\,\mathrm{km}$ . En ese caso, la velocidad resultante sería

$v = \sqrt{2gh}= \sqrt{2\cdot 9.8\frac{\mathrm{m}}{\mathrm{s}^2}\cdot 10\,\mathrm{km}} = 14\,\frac{\sqrt{\mathrm{km}}\sqrt{\mathrm{m}}}{\mathrm{s}}$

Este resultado, aunque algebraicamente correcto, no posee una forma conveniente por la aparición de potencias fraccionarias de las unidades. Por ello, debe procurarse que el uso de las unidades sea consistente. Expresando la altura en metros

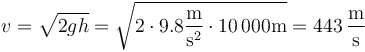
$v = \sqrt{2gh}= \sqrt{2\cdot 9.8\frac{\mathrm{m}}{\mathrm{s}^2}\cdot 10\,000\mathrm{m}} = 443\,\frac{\mathrm{m}}{\mathrm{s}}$

Este ejemplo ilustra los peligros de sustituir los valores numéricos de las magnitudes sin incluir sus unidades correspondientes. Una respuesta tal como “14” sin más datos, a la pregunta de cuál es la velocidad, sería absolutamente errónea.

2.2 El Sistema Internacional de Unidades

Este sistema de unidades es de obligado cumplimiento en España de acuerdo con el R.D. 2032/2009 (BOE del 21/01/2010, revisado el 18/02/2010).

El SI se basa en siete unidades básicas:

Magnitud	Unidad	Abreviatura
Longitud	metro	m
Masa	kilogramo	kg
Tiempo	segundo	s
Intensidad de corriente	amperio	A
Temperatura	kelvin	K
Cantidad de sustancia	mol	mol
Intensidad luminosa	candela	cd

A partir de estas unidades básicas se construyen una infinitud de unidades derivadas, mediante productos de potencias de las unidades básicas. Muchas de estas unidades poseen nombre propio, así por ejemplo, 1 hercio (Hz) es igual a 1 s⁻¹, 1 newton (N) es igual a 1kg·m/s² y 1 julio (J) equivale a 1kg·m²/s².

Para obtener unidades derivadas en el SI, basta aplicar las ecuaciones dimensionales. Así, para las magnitudes anteriores

Magnitud	Dimensiones	Unidad SI
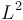
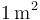
Área	$L^2\,$	$1\,\mathrm{m}^2\,$
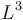
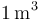
Volumen	$L^3\,$	$1\,\mathrm{m}^3\,$
Velocidad	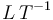$L\,T^{-1}\,$	$\,\mathrm{m}/\mathrm{s}\,$
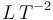
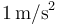
Aceleración	$L\,T^{-2}\,$	$1\,\mathrm{m}/\mathrm{s}^2\,$
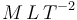
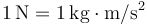
Fuerza	$M\,L\,T^{-2}\,$	$1\,\mathrm{N}=1\,\mathrm{kg}\cdot\mathrm{m}/\mathrm{s}^2\,$
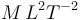
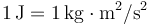
Trabajo	$M\,L^2T^{-2}\,$	$1\,\mathrm{J}=1\,\mathrm{kg}\cdot\mathrm{m}^2/\mathrm{s}^2\,$
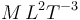
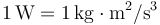
Potencia	$M\,L^2T^{-3}\,$	$1\,\mathrm{W}=1\,\mathrm{kg}\cdot\mathrm{m}^2/\mathrm{s}^3\,$

Mención especial merecen una unidad adimensional: el radián.

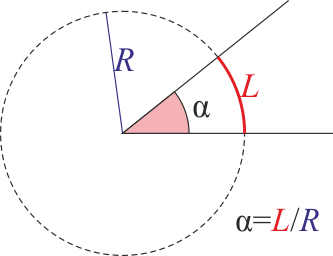
Un ángulo medido en radianes se define como el cociente entre la longitud de un arco de circunferencia y el radio de dicha circunferencia

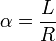
$\alpha = \frac{L}{R}$

y por tanto

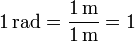
$1\,\mathrm{rad} = \frac{1\,\mathrm{m}}{1\,\mathrm{m}} = 1$

esto es, el radián es una forma diferente de llamar a la unidad, aportando información sobre la magnitud que miden. Así en la relación entre la frecuencia angular ω y la frecuencia natural f

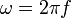
$\omega = 2\pi f\,$

la primera magnitud de mide en rad/s, mientras que la segunda se mide en Hz = 1/s. Esta ecuación es dimensionalmente correcta, por ser adimensional el radián. Esto quiere decir, en la práctica, que el radián es una unidad que puede aparecer y desaparecer de las ecuaciones a voluntad.

2.3 Múltiplos y submúltiplos

Las unidades del SI pueden resultar demasiado grandes o demasiado pequeñas para un problema concreto, por lo que se suelen acompañar de prefijos que indican múltiplos o submúltiplos

Prefijo	Símbolo	10ⁿ	Prefijo	Símbolo	10ⁿ
deca	da	10¹	deci	d	10⁻¹
hecto	h	10²	centi	c	10⁻²
kilo	k	10³	mili	m	10⁻³
mega	M	10⁶	micro	μ	10⁻⁶
giga	G	10⁹	nano	n	10⁹
tera	T	10¹²	pico	p	10⁻¹²
peta	P	10¹⁵	femto	f	10⁻¹⁵
exa	E	10¹⁸	atto	a	10⁻¹⁸
zetta	Z	10²¹	zepto	z	10⁻²¹
yotta	Y	10²⁴	yocto	y	10⁻²⁴

Muchas unidades que son realmente múltiplos de unidades fundamentales poseen nombre propio. Así, por ejemplo 1 hectárea (Ha) es igual a 10000 m² y 1 gramo es igual a 0.001 kg (siendo el kilogramo la unidad fundamental).

2.4 Conversión de unidades

Es frecuente la necesidad de transformar una magnitud expresada en ciertas unidades a un sistema de unidades diferente. La forma más sistemática de realizar esta operación es con la ayuda de factores de conversión, que son fracciones cuyo numerador y denominador corresponden al mismo valor de una magnitud, expresada en unidades diferentes. Para transformar una expresión de un sistema a otro se multiplica por los factores de conversión necesarios hasta que el resultado final queda en las unidades deseadas, una vez que se cancelen las unidades que aparecen en las diferentes fracciones.

Así, para pasar de km/h a m/s el procedimiento sería

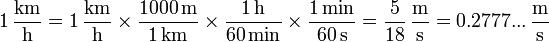
$1\,\frac{\mathrm{km}}{\mathrm{h}} = 1\,\frac{\mathrm{km}}{\mathrm{h}}\times\frac{1000\,\mathrm{m}}{1\,\mathrm{km}}\times\frac{1\,\mathrm{h}}{60\,\mathrm{min}}\times \frac{1\,\mathrm{min}}{60\,\mathrm{s}} = \frac{5}{18}\,\frac{\mathrm{m}}{\mathrm{s}} = 0.2777...\,\frac{\mathrm{m}}{\mathrm{s}}$

Obsérvese que es importante que los factores en los numeradores y denominadores se cancelen correctamente.

Un procedimiento sistemático para abordar un problema en el que los diferentes datos se den en unidades de sistemas diferentes, consiste en primer lugar en transformar todas las cantidades al SI, operar exclusivamente en este sistema (aunque ello implique el uso de numerosas potencias de 10) y finalmente transformar el resultado final a aquellas unidades que resulten más convenientes.

Dimensiones y unidades (GIOI)

De Laplace

Contenido

1 Dimensiones

1.1 Medidas directas e indirectas

1.2 Dimensiones de una magnitud

1.3 Homogeneidad dimensional

1.4 Ecuaciones dimensionales

2 Unidades de medida

2.1 Homogeneidad en las unidades

2.2 El Sistema Internacional de Unidades

2.3 Múltiplos y submúltiplos

2.4 Conversión de unidades

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES