Descenso por plano con resorte (GIE)
De Laplace
Contenido |
1 Enunciado
En un plano inclinado de 16 cm de base y 12 cm se altura se halla, unido al extremo inferior del plano, un resorte de constante  y longitud natural
y longitud natural 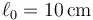 .
.

Desde lo alto del plano se suelta una masa 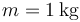 .
.
- Determine en la posición (medida desde la esquina inferior del plano) en que se detiene una vez que impacta con el resorte si no hay rozamiento con el suelo.
- Suponga ahora que existe un coeficiente de rozamiento μ = 0.60 entre la masa y el plano inclinado. Calcule para este caso la posición en que se detiene la masa suponiendo igualmente que se suelta desde el punto superior.
- Para el caso con rozamiento, calcule la posición hasta la que llega a la masa tras rebotar en el muelle y volver a subir.
Dato: Tómese 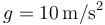 .
.
2 Detención sin rozamiento
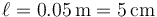
3 Detención con rozamiento

4 Segunda detención con rozamiento