Cuestión sobre Sólidos en Contacto, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Par cinemático
- 2.2 Número de grados de libertad

1 Enunciado

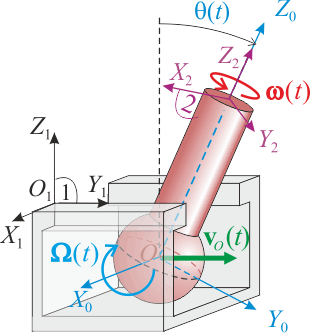
Los sólidos rígidos de la figura se encuentran en contacto, por lo que su movimiento relativo está sometido a ciertas restricciones. El extremo esférico del sólido “2” está obligado a permanecer en el interior del carril (sólido “1”), pudiendo desplazarse sólo a lo largo de su dirección longitudinal (paralela al eje

O 1 Y 1

). Por otra parte, el sólido “2” no puede ejecutar giros en torno a dicha dirección debido a que el vástago cilíndrico está insertado en la ranura del sólido “1”.

Obtenga razonadamente el par cinemático (reducción cinemática en $O$ ) que describe de forma general el movimiento instantáneo permitido al sólido “2” respecto del carril (sólido “1”).
¿Cuál es el número de grados de libertad del sistema? Justifique su respuesta.

2 Solución

2.1 Par cinemático

Para obtener una reducción cinemática que describa en cada instante el movimiento relativo de estos sólidos en contacto, resulta conveniente introducir un sistema de referencia auxiliar $O X 0 Y 0 Z 0$ , que constituirá el sólido rígido “0”. Tomaremos como origen de dicho sistema cartesiano el punto $O$ del sólido “2” en el cuál nos piden que hagamos la reducción, y adoptaremos como dirección $O Z 0$ el eje de simetría de dicho sólido, coincidiendo con el $O Z 2$ propuesto en la figura del enunciado. Además, adoptaremos un eje $O X 0$ paralelo en todo instante con el eje $O 1 X 1$ solidaria con el carril o sólido “1”.

2.1.1 Reducción cinemática del movimiento {01}

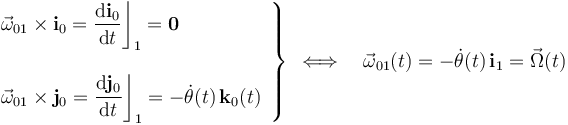
Según hemos definido el sólido “0”, éste se moverá respecto del sólido fijo “1” de manera que el punto

O

sólo puede desplazarse en la dirección del eje

O 1 Y 1

, de manera que, en un instante de tiempo arbitrario

t

, la velocidad de dicho punto en el movimiento

{01}

será: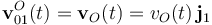 $\mathbf{v}_{01}^O(t)=\mathbf{v}_O(t)=v_O(t)\!\ \mathbf{j}_1$

Las siguientes expresiones describen los vectores ortonormales asociados a los ejes cartesianos $O X 0 Y 0 Z 0$ , en términos de la base ortonormal de los ejes fijos $O 1 X 1 Y 1 Z 1$ :

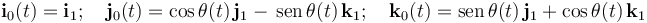
$\mathbf{i}_0(t)=\mathbf{i}_1\mathrm{;}\,\quad\mathbf{j}_0(t)=\cos\theta(t)\!\ \mathbf{j}_1-\,\mathrm{sen}\,\theta(t)\!\ \mathbf{k}_1\mathrm{;}\,\quad\mathbf{k}_0(t)=\mathrm{sen}\,\theta(t)\!\ \mathbf{j}_1+\cos\theta(t)\!\ \mathbf{k}_1$

siendo $θ(t)$ el ángulo que forma el eje de simetría del sólido “2” (es decir, el 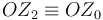$OZ_2\equiv OZ_0$ ), con la dirección vertical paralela al eje fijo $O 1 Z 1$ . La aplicación de las fórmulas de Poisson en estas expresiones es una forma muy efectiva de obtener el vector rotación $\vec{\omega}_{01}$ que completa la descripción del movimiento instanténeo del sólido “0” respecto del carril “1”:

$\left.\begin{array}{l}\displaystyle\vec{\omega}_{01}\times\mathbf{i}_0=\frac{\mathrm{d}\mathbf{i}_0}{\mathrm{d}t}\bigg\rfloor_1=\mathbf{0}\\ \\ \displaystyle\vec{\omega}_{01}\times\mathbf{j}_0=\frac{\mathrm{d}\mathbf{j}_0}{\mathrm{d}t}\bigg\rfloor_1=-\dot{\theta}(t)\!\ \mathbf{k}_0(t)\end{array}\right\}\,\; \Longleftrightarrow\quad \vec{\omega}_{01}(t)=-\dot{\theta}(t)\!\ \mathbf{i}_1=\vec{\Omega}(t)$

2.1.2 Reducción cinemática del movimiento {20}

Por su parte, en el movimiento del sólido “2” respecto del sistema de referencia auxiliar que hemos introducido, el punto $O$ permanece en reposo permanente, ya que se trata de un punto fijo de aquél en el cuál situamos en todo instante el origen del sistema de referencia $O X 0 Y 0 Z 0$ :

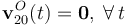
$\mathbf{v}_{20}^O(t)=\mathbf{0}\mathrm{,}\,\;\forall\, t$

Al hacer coincidir en todo instante los ejes $O Z 0$ y $O Z 2$ , las direcciones $O X 2$ y $O Y 2$ formarán el mismo ángulo $\varphi (t)$ con los respectivos ejes $O X 0$ y $O Y 0$ , en un instante arbitrario $t$ . Por tanto, se tendrá:

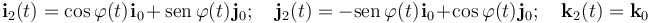
$\mathbf{i}_2(t)=\cos\varphi(t)\!\ \mathbf{i}_0+\,\mathrm{sen}\,\varphi(t)\!\ \mathbf{j}_0\mathrm{;}\,\quad\mathbf{j}_2(t)=-\mathrm{sen}\,\varphi(t)\!\ \mathbf{i}_0+\cos\varphi(t)\!\ \mathbf{j}_0\mathrm{;}\,\quad\mathbf{k}_2(t)=\mathbf{k}_0$

Aplicando nuevamente las fórmulas de Poisson al caso del movimiento ${20}$ , obtenemos la expresión del correspondiente vector rotación instantánea $\vec{\omega}_{01}$ :

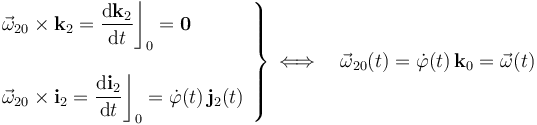
$\left.\begin{array}{l}\displaystyle\vec{\omega}_{20}\times\mathbf{k}_2=\frac{\mathrm{d}\mathbf{k}_2}{\mathrm{d}t}\bigg\rfloor_0=\mathbf{0}\\ \\ \displaystyle\vec{\omega}_{20}\times\mathbf{i}_2=\frac{\mathrm{d}\mathbf{i}_2}{\mathrm{d}t}\bigg\rfloor_0=\dot{\varphi}(t)\!\ \mathbf{j}_2(t)\end{array}\right\}\, \Longleftrightarrow\quad \vec{\omega}_{20}(t)=\dot{\varphi}(t)\!\ \mathbf{k}_0=\vec{\omega}(t)$

2.1.3 Reducción cinemática del movimiento {21}

Aplicando las expresiones para la composición de movimientos, obtenemos la reducción cinemática 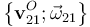$\big\{\mathbf{v}_{21}^O\mathrm{;}\,\vec{\omega}_{21}\big\}$ (par cinemático) que describe el movimiento instanténeo permitido al sólido “2” respecto del carril “1”, cuando ambos se hayan en contacto:

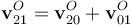
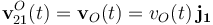
$\mathbf{v}_{21}^O=\mathbf{v}_{20}^O+\mathbf{v}_{01}^O$ $\Rightarrow$ $\mathbf{v}_{21}^O(t)=\mathbf{v}_O(t)=v_O(t)\!\ \mathbf{j_1}$

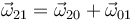
$\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}$ $\Rightarrow$ $\vec{\omega}_{21}(t)=\vec{\Omega} (t)+\vec{\omega}(t)=-\dot{\theta}(t)\!\ \mathbf{i_1}+\dot{\varphi}(t)\!\ \big[ \mathrm{sen}\,\theta(t)\!\ \mathbf{j}_1+\cos\theta(t)\!\ \mathbf{k}_1\big]$

2.2 Número de grados de libertad

En virtud del teorema de Chasles, la velocidad instantánea en el movimiento ${21}$ de un punto arbitrario del sólido “2” estará determinada por la reducción cinemática anterior, según la ley,

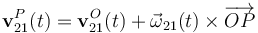
$\mathbf{v}_{21}^P(t)=\mathbf{v}_{21}^O(t)+\vec{\omega}_{21}(t)\times\overrightarrow{OP}$

por el que el desplazamiento inifitesimal instantáneo de dicho punto arbitrario puede expresarse como la superposición de una traslación 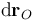$\mathrm{d}\mathbf{r}_O$ paralela al desplazamiento del punto $O$ , y una rotación infitesimal 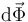$\mathrm{d}\vec{\Phi}$ alrededor de un eje que pasa por dicho punto $O$ y tiene la dirección del vector rotación $\vec{\omega}_{21}$ en el instante considerado:

$\mathrm{d}\mathbf{r}_P=\mathbf{v}_{21}^P(t)\!\ \mathrm{d}t=\mathrm{d}\mathbf{r}_O+\mathrm{d}\vec{\Phi}\times\overrightarrow{OP}\mathrm{,}\,\quad\mathrm{con}\,\quad\;\begin{cases}\displaystyle \mathrm{d}\mathbf{r}_O=\mathbf{v}_{21}^O(t)\!\ \mathrm{d}t=\mathrm{d}y_O\!\ \mathbf{j}_1\\ \\ \mathrm{d}\vec{\Phi}=\vec{\omega}_{21}(t)\!\ \mathrm{d}t=- \mathrm{d}\theta\!\ \mathbf{j}_1+ \mathrm{d}\varphi\!\ \big[ \mathrm{sen}\,\theta(t)\!\ \mathbf{j}_1+\cos\theta(t)\!\ \mathbf{k}_1\big]\end{cases}$

Es decir, el desplazamiento de cualquier punto del sólido “2” respecto del carril “1” puede expresarse como el resultado de la variación de tres parámetros geométricos distintos, variables en el tiempo e independientes entre sí:

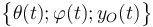
$\big\{\theta (t)\mathrm{;}\,\varphi (t)\mathrm{;}\,y_O(t)\big\}$

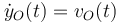A saber, los ángulos $θ(t)$ y $\varphi (t)$ , descritos en el apartado anterior de este ejercicio, y la coordenada $y O (t)$ del centro $O$ de la esfera que forma parte del sólido “2”, y es tal que $\dot{y}_O(t)=v_O(t)$ . Por tanto, la restricciones impuestas por el contacto real entre los sólidos “1” y “2”, reduce a 3 el número de grados de libertad existentes en el movimiento relativo de ambos sólidos.

Cuestión sobre Sólidos en Contacto, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Par cinemático

2.1.1 Reducción cinemática del movimiento {01}

2.1.2 Reducción cinemática del movimiento {20}

2.1.3 Reducción cinemática del movimiento {21}

2.2 Número de grados de libertad

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES