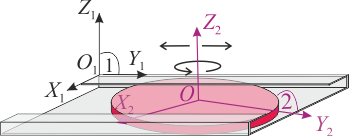
Cuestión de cinemática: sólidos en contacto, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Par cinemático
- 2.2 Número de grados de libertad

1 Enunciado

Determinar el par cinemático (reducción cinemática en

O

) que describe de forma general el movimiento permitido a un disco (sólido “2”) obligado a desplazarse encajado en un carril (sólido “1”) cuya anchura coincide con el diámetro del disco. ¿Cuál es el número de grados de libertad del sistema? Justifique sus respuestas.

2 Solución

El movimiento instantáneo del disco (sólido “2”), respecto del carril que se considera fijo (sólido “1”) estará caracterizado por la correspondiente reducción cinemática,

$S_{21}\equiv\left\{\begin{array}{l}\displaystyle\vec{\omega}_{21}(t)=\omega_x(t)\!\ \vec{\imath}_1+\omega_y(t)\!\ \vec{\jmath}_1+\omega_z(t)\!\ \vec{k}_1\\ \\ \displaystyle\vec{v}_{21}^O(t)=v_x(t)\!\ \vec{\imath}_1+v_y(t)\!\ \vec{\jmath}_1+v_z(t)\!\ \vec{k}_1 \end{array}\right.$

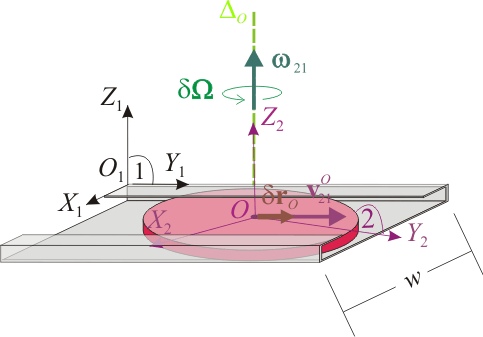
donde se propone como centro de reducción el punto $O$ (es decir, el centro del disco). El contacto real entre ambos cuerpos materiales establece una serie de condiciones para los movimientos relativos de ambos sólidos, que reducirán el número de grados de libertad del sólido “2”, y que determinarán las propiedades del par cinemático (reducción cinemática). Si en un intervalo de tiempo infinitesimal $d t$ , las restricciones al movimiento del disco debido al contacto con el carril son tales que el punto $O$ sólo puede realizar un determinado desplazamiento 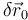$\delta \vec{r}_0$ , y el disco sólo puede realizar un determinado giro infinitesimal que representamos por 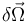$\delta \vec{\Omega}$ , en torno a un eje $Δ O$ que pasa por el centro de reducción, los elementos de la reducción o par cinemático deben ser tales que:

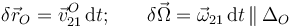
$\delta\vec{r}_O=\vec{v}_{21}^O\!\ \mathrm{d}t\mathrm{;}\qquad\delta \vec{\Omega}=\vec{\omega}_{21}\!\ \mathrm{d}t\!\ \|\!\ \Delta_O$

2.1 Par cinemático

En el sistema analizando, el disco esta obligado a moverse en el carril cuya anchura es igual al diámetro del disco ( $w = 2 R$ ). Por tanto, la posición del centro del disco estará descrita, en el sistema de referencia ligado al sólido “1”, por el radiovector

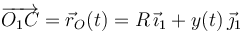
$\overrightarrow{O_1C}=\vec{r}_O(t)=R\!\ \vec{\imath}_1+y(t)\!\ \vec{\jmath}_1$

Es decir, las componentes “ $x$ ” y “ $z$ ” de dicho punto van a tener valores constantes ( $R$ y $0$ , respectivamente), y sólo la componente “ $y$ ” va a ser variable con el movimiento del disco, se tendrá, por tanto:

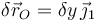
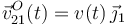
$\delta\vec{r}_O=\delta y\!\ \vec{\jmath}_1$ $\quad$ $\Rightarrow$ $\quad$ $\vec{v}_{21}^O(t)=v(t)\!\ \vec{\jmath}_1$

En cuanto al vector rotación instantánea, tenemos que el disco está obligado a moverse contenido en un plano paralelo al plano fijo $O 1 X 1 Y 1$ . Si adoptamos un sistema de referencia $O X 2 Y 2 Z 2$ solidario con el sólido “2”, de manera que el eje $O Z 2$ sea perpendicular al disco:

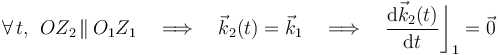
$\forall\, t\mathrm{,}\;\;OZ_2\!\ \|\!\ O_1Z_1\quad\Longrightarrow\quad\vec{k}_2(t)=\vec{k}_1\quad\Longrightarrow\quad\frac{\mathrm{d}\vec{k}_2(t)}{\mathrm{d}t}\bigg\rfloor_1=\vec{0}$

Si aplicamos la fórmulas de Poisson, se tendrá:

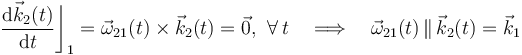
$\frac{\mathrm{d}\vec{k}_2(t)}{\mathrm{d}t}\bigg\rfloor_1=\vec{\omega}_{21}(t)\times\vec{k}_2(t)=\vec{0}\mathrm{,}\;\;\forall\, t\quad\Longrightarrow\quad\vec{\omega}_{21}(t)\!\ \|\!\ \vec{k}_2(t)=\vec{k}_1$

Es decir, las únicas rotaciones permitidas al sólido “2” son aquéllas que realice en torno a ejes perpendiculares al disco:

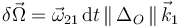
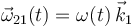
$\delta \vec{\Omega}=\vec{\omega}_{21}\!\ \mathrm{d}t\!\ \|\!\ \Delta_O\!\ \|\!\ \vec{k}_1$ $\quad$ $\Rightarrow$ $\quad$ $\vec{\omega}_{21}(t)=\omega(t)\!\ \vec{k}_1$

2.2 Número de grados de libertad

Hemos determinado que el par cinemático que describiría en cada instante el movimiento permitido al disco respecto del carril, es de la forma:

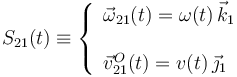
$S_{21}(t)\equiv\left\{\begin{array}{l}\vec{\omega}_{21}(t)=\omega(t)\!\ \vec{k}_1\\ \\ \vec{v}_{21}^O(t)=v(t)\!\ \vec{\jmath}_1\end{array}\right.$

donde las leyes horarias $ω(t)$ , para la componente “ $z$ ” del vector rotación instantánea, y $v (t)$ para la componente “ $y$ ” de la velocidad del centro del disco, estarán determinadas por las fuerzas (no vinculares) que actúen sobre el disco. Por el contrario, la condición de contacto entre los dos sólidos reales, condicionan a priori los valores de las otras componentes de los elementos de la reducción. Concretamente, hemos comprobado que dichas componentes van a ser nulas en todo instante. Por tanto, tenemos cuatro condiciones distintas para las componentes de la reducción cinemática instantánea $S 21$ , derivadas de las restricciones impuestas por dicho contacto, y que reducen a dos los seis grados de libertad correspondientes al caso del sólido rígido no sometido a vínculos:

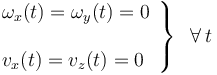
$\left.\begin{array}{l}\omega_x(t)=\omega_y(t)=0\\ \\ v_x(t)=v_z(t)=0 \end{array}\right\}\;\;\forall\, t$ $\quad$ $\Rightarrow$ $\quad$

n . g . l . = 6 - 4 = 2

Cuestión de cinemática: sólidos en contacto, Diciembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Par cinemático

2.2 Número de grados de libertad

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES