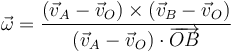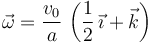Cuestión de cinemática: campo de velocidades de S.R., Diciembre 2012 (F1 GIA)

De Laplace

1 Enunciado

Determine los valores de los parámetros λ, μ y ν para que los vectores

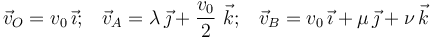
describan las velocidades instantáneas de tres puntos de un sólido rígido, cuyas posiciones están dadas por las ternas de coordenadas cartesianas, O(0,0,0), A(0,a,0) y B(0,0,b). Calcule también las componentes del correspondiente vector rotación instantánea.

2 Solución

2.1 Condición de equiproyectividad

Para que un conjunto de vectores 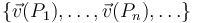, describan las velocidades instantáneas de sendos puntos 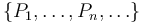de un sólido rígido τ en movimiento, es condición suficiente y necesaria que dicho campo de velocidades sea equiproyectivo; es decir,

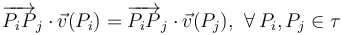
Por tanto, para resolver este ejercicio debemos determinar los valores de los parámetros λ, μ y ν que hagan que los vectores 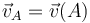, 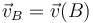y 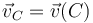, verifiquen simultáneamente la propiedad de equiproyectividad.

Calculamos previamente los segmentos orientados que describen las posiciones relativas de cada par de puntos. Y puesto que el punto O coincide con el origen del sistema de referencia cartesiano que utilizaremos para describir analíticamente todas las magnitudes vectoriales del sistema, se tendrá:

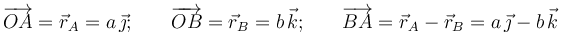
Nótese que si O, A y B son tres puntos distintos del sólido, es necesario que los valores a y b sean estrictamente distintos de cero.

Exigimos ahora que se verifique la propiedad de equiproyectividad para cada par de puntos:

              

              

              

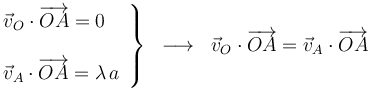
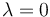
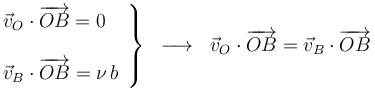
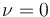
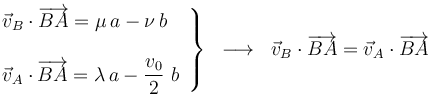
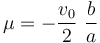
2.2 Vector rotación instantáneo

Los valores de los parámetros calculados en el apartado anterior nos proporcionan las velocidades instantáneas de tres puntos de un sólido rígido que, en un cierto instante, ocupan las posiciones dadas por las ternas cartesianas O(0,0,0), A(0,a,0) y B(0,0,b):

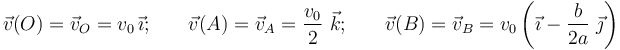
Por tanto, estas magnitudes vectoriales deben verificar el teorema de Chasles:

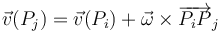
donde el vector rotación característico del movimiento instantáneo del sólido.

Aprovechando que los tres puntos no están alineados y que sus correspondientes velocidades son distintas, podemos realizar la siguiente operación:

Y a partir de esta expresión, podemos calcular el vector rotación instantánea, utilizando magnitudes vectoriales de valor conocido: