Corriente de desplazamiento en un condensador plano GIA

De Laplace

1 Enunciado

Tenemos un condensador plano de placas circulares de radio 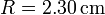$R= 2.30\,\mathrm{ cm}$ separadas par una distancia 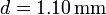$d=1.10\,\mathrm{mm}$ . Al condensador llega una corriente 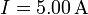$I=5.00\,\mathrm{A}$ . Calcula la corriente de desplazamiento en el interior del condensador.

2 Solución

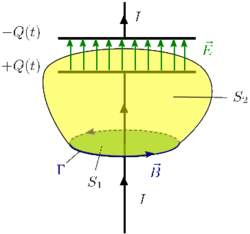
La corriente que llega al condensador provoca que en una de sus placas aparezca una carga $Q (t)$ . Esta carga crea un campo eléctrico entre las cargas y produce una carga $- Q (t)$ en la placa opuesta, pues ambas placas están en influencia total. Este campo eléctrico depende del tiempo, y la corriente de desplazamiento es proporcional a la derivada en el tiempo del flujo eléctrico de este campo. Si llamamos $I 0$ a la corriente que llega a las placas tenemos

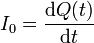
$I_0 = \dfrac{\mathrm{d}Q(t)}{\mathrm{d}t}$

Esto es así por que la carga que lleva la corriente no puede atravesar el condensador y queda depositada en la placa del condensador.

Como el radio de las placas del condensador es mucho menor que la distancia que las separa (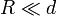 $R\ll d$ ), está justificado despreciar los efectos de borde. Suponemos entonces que el campo eléctrico entre las placas del condensador es uniforme y perpendicular a las placas

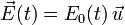
$\vec{E}(t) = E_0(t)\,\vec{u}$

El vector $\vec{u}$ es un vector unitario que va desde la placa con carga positiva a la negativa.

Vimos en el tema dos que el campo creado entre dos placas con densidades de carga del mismo valor absoluto y signos contrarios era

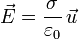
$\vec{E} = \dfrac{\sigma}{\varepsilon_0}\,\vec{u}$

donde $σ$ es la densidad superficial de carga. En nuestro caso la densidad superficial de carga es

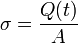
$\sigma = \dfrac{Q(t)}{A}$

siendo 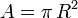$A=\pi\,R^2$ el área de las placas del condensador. Entonces el campo eléctrico entre las placas puede escribirse

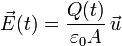
$\vec{E}(t) = \dfrac{Q(t)}{\varepsilon_0A}\,\vec{u}$

Vamos a calcular la corriente de desplazamiento que atraviesa el condensador. El flujo eléctrico a través de una superficie paralela a las placas es

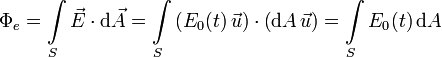
$\Phi_e = \int\limits_S\vec{E}\cdot\mathrm{d}\vec{A} = \int\limits_S\left(E_0(t)\,\vec{u}\right)\cdot\left(\mathrm{d}A\,\vec{u}\right)= \int\limits_SE_0(t)\,\mathrm{d}A$

Como el campo eléctrico es uniforme tenemos

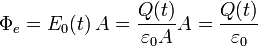
$\Phi_e = E_0(t)\,A = \dfrac{Q(t)}{\varepsilon_0A}A = \dfrac{Q(t)}{\varepsilon_0}$

La corriente de desplazamiento es

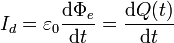
$I_d = \varepsilon_0\dfrac{\mathrm{d}\Phi_e}{\mathrm{d}t} = \dfrac{\mathrm{d}Q(t)}{\mathrm{d}t}$

Pero este valor es igual a la corriente que llega a las placas.

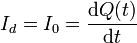
$I_d = I_0 = \dfrac{\mathrm{d}Q(t)}{\mathrm{d}t}$

Vemos entonces que la corriente de desplazamiento entre las placas del condensador es igual a la corriente de conducción en el cable. Este hecho es el que hace que la Ley de Ampère-Maxwell pueda aplicarse a cualquier superficie apoyada en una curva cerrada. La Ley es

$\oint\limits_{\Gamma} \vec{B}\cdot\mathrm{d}\vec{l} = \mu_0\left[I+I_d\right]_{S_{\Gamma}}$

En el sistema de la figura, consideramos dos superficies apoyadas en la curva cerrada $Γ$ . Si aplicamos la Ley de Ampère en la superficie $S 1$ tenemos

$\oint\limits_{\Gamma} \vec{B}\cdot\mathrm{d}\vec{l} = \mu_0\left[I+I_d\right]_{S_{1}}= \mu_0\,I_0$

Mientras que si lo hacemos en la superficie dos tenemos

$\oint\limits_{\Gamma} \vec{B}\cdot\mathrm{d}\vec{l} = \mu_0\left[I+I_d\right]_{S_{2}}= \mu_0\,I_d= \mu_0\,I_0$

Hay que señalar que el hecho de que la corriente de conducción en el cable y la corriente de desplazamiento en el interior del condensador sean numéricamente iguales no quiere decir que podamos escribir la Ley de Ampère-Maxwell así

$\oint\limits_{\Gamma} \vec{B}\cdot\mathrm{d}\vec{l} = \mu_0\left[I+I_d\right]_{S_{\Gamma}}= \mu_0\left[2\,I_0 \right]_{S_{\Gamma}}$

Esto no es correcto. La corriente de conducción y la de desplazamiento aparecen en lugares distintos. La de conducción en el cable y la de desplazamiento en el interior del condensador.

Corriente de desplazamiento en un condensador plano GIA

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES