Conos Segunda Prueba de Control (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Dos conos rectos de semiángulos en el vértice $π / 3$ y $π / 6$ (sólidos "0" y "2", respectivamente), se hallan en contacto en todo instante por una generatriz. Cada cono realiza un movimiento de rotación permanente respecto a un sistema de referencia fijo (sólido "1") alrededor de su correspondiente eje de simetría. Las velocidades angulares respectivas son 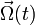$\vec{\Omega}(t)$ para el movimiento {01} y 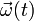$\vec{\omega}(t)$ para el {21}. Además, los conos se mueven de manera que sus puntos en contacto no tienen deslizamiento relativo.

¿Que tipo de movimiento es el {20}?
En ese movimiento, ¿que puntos tienen velocidad mínima?
¿Que relación deben cumplir las velocidades angulares del enunciado?
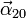Calcula la aceleración angular $\vec{\alpha}_{20}$ .

2 Solución

2.1 Tipo de movimiento

Todos los puntos de las generatrices que están en contacto tienen velocidad relativa nula en el movimiento {20}, mientras que los que no están en las generatrices no. Por tanto el movimiento {20} es una rotación. El eje instantáneo de esta rotación cambia con el tiempo desde el punto de vista de los conos, por lo que la rotación es instantánea.

2.2 Puntos con velocidad mínima en el movimiento {20}

Por lo explicado en el apartado anterior, los puntos de la generatrices en contacto tienen velocidad relativa nula, por tanto son los puntos con velocidad mínima.

2.3 Relación de las velocidades angulares

Vamos a reducir los movimientos de los conos

En el movimiento {01} tenemos

$\vec{\omega}_{01} = \Omega\,\vec{k}_1 \qquad \qquad \vec{v}\,^O_{01} = \vec{0}$

En el movimiento {21} tenemos

$\vec{\omega}_{21} = \omega\,\vec{\imath}_1 \qquad \qquad \vec{v}\,^O_{21} = \vec{0}$

Usando la composición de velocidades angulares

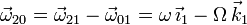
$\vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = \omega\,\vec{\imath}_1 - \Omega\,\vec{k}_1$

Este vector debe ser paralelo a las generatrices en contacto de los conos. Del dibujo vemos que un vector paralelo a esta generatriz es

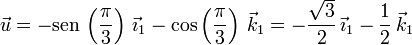
$\vec{u} = -\mathrm{sen}\,\left(\dfrac{\pi}{3}\right)\,\vec{\imath}_1-\cos\left(\dfrac{\pi}{3}\right)\,\vec{k}_1 = -\dfrac{\sqrt{3}}{2}\,\vec{\imath}_1 - \dfrac{1}{2}\,\vec{k}_1$

Para que la dirección del eje instantáneo sea paralela a la generatriz debe ocurrir

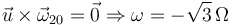
$\vec{u}\times\vec{\omega}_{20}=\vec{0} \Rightarrow \omega = -\sqrt{3}\,\Omega$

2.4 Aceleración angular

Derivamos $\vec{\omega}_{20}$ respecto al tiempo para obtener la aceleración.

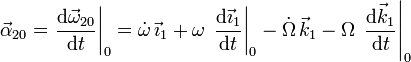
$\vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0 = \dot{\omega}\,\vec{\imath}_1 + \omega\,\left.\dfrac{\mathrm{d}\vec{\imath}_1}{\mathrm{d}t}\right|_0 -\dot{\Omega}\,\vec{k}_1 - \Omega\,\left.\dfrac{\mathrm{d}\vec{k}_1}{\mathrm{d}t}\right|_0$

Usamos las fórmulas de Poisson para hacer las derivadas de los vectores de la base del sólido "1". Por un lado

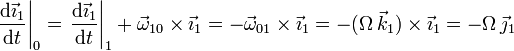
$\left.\dfrac{\mathrm{d}\vec{\imath}_1}{\mathrm{d}t}\right|_0 = \left.\dfrac{\mathrm{d}\vec{\imath}_1}{\mathrm{d}t}\right|_1 + \vec{\omega}_{10}\times\vec{\imath}_1 = -\vec{\omega}_{01}\times\vec{\imath}_1 = -(\Omega\,\vec{k}_1)\times\vec{\imath}_1 = -\Omega\,\vec{\jmath}_1$

Por otro

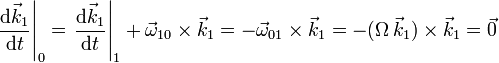
$\left.\dfrac{\mathrm{d}\vec{k}_1}{\mathrm{d}t}\right|_0 = \left.\dfrac{\mathrm{d}\vec{k}_1}{\mathrm{d}t}\right|_1 + \vec{\omega}_{10}\times\vec{k}_1 = -\vec{\omega}_{01}\times\vec{k}_1 = -(\Omega\,\vec{k}_1)\times\vec{k}_1 = \vec{0}$

Así pues, la aceleración angular pedida es

$\vec{\alpha}_{20} = \dot{\omega}\,\vec{\imath}_1 - \omega\,\Omega\,\vec{\jmath}_1 - \dot{\Omega}\,\vec{k}_1$

Conos Segunda Prueba de Control (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Tipo de movimiento

2.2 Puntos con velocidad mínima en el movimiento {20}

2.3 Relación de las velocidades angulares

2.4 Aceleración angular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES