Composición de dos rotaciones de 90° (CMR)

De Laplace

Contenido

1 Enunciado
2 Introducción
3 Primer caso
4 Segundo caso
5 Tercer caso

1 Enunciado

Se tiene un sólido situado de tal manera que inicialmente los sistemas de referencia fijo, “1” y ligado, “2”, coinciden.

Supongamos que el sólido se hace girar en primer lugar +90° en torno a $O Y 1$ y a continuación −90° en torno a un eje paralelo a $O Y 1$ por 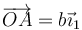$\overrightarrow{OA}=b\vec{\imath}_1$ . ¿Cuál es el resultado de esta composición de movimientos?
Supongamos que el sólido se hace girar en primer lugar +90° en torno a $O Y 1$ y a continuación +90° en torno a un eje paralelo a $O Y 1$ por 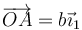$\overrightarrow{OA}=b\vec{\imath}_1$ . ¿Cuál es el resultado de esta composición de movimientos?
Supongamos que el sólido se hace girar en primer lugar +90° en torno a $O Y 1$ y a continuación −90° en torno a un eje paralelo a $O Z 1$ por 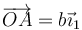$\overrightarrow{OA}=b\vec{\imath}_1$ . ¿Cuál es el resultado de esta composición de movimientos?

2 Introducción

Cuando se tiene una rotación alrededor del origen, la transformación entre las coordenadas de un punto en el sistema ligado $(X, Y, Z)$ y sus coordenadas en el sistema fijo $(x, y, z)$ las da la matriz de rotación 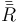$\bar{\bar{R}}$

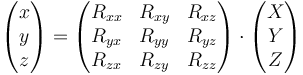
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}R_{xx}& R_{xy}&R_{xz}\\ R_{yx}&R_{yy}&R_{yz}\\ R_{zx}&R_{zy}&R_{zz}\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix}$

Si los ejes de los dos sistemas son coincidentes inicialmente, lo que ocurre a menudo, esta ecuación también nos da la relación entre las coordenadas antes y después de la rotación

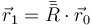
$\vec{r}_1=\bar{\bar{R}}\cdot\vec{r}_0$

o, usando vectores de posición relativa

$\overrightarrow{OP}^{\prime}=\bar{\bar{R}}\cdot\overrightarrow{OP}$

Si la rotación no se produce alrededor del origen sino de un eje que pasa por un punto E, la expresión es la misma, pero respecto a dicho punto

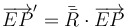
$\overrightarrow{EP}^{\prime}=\bar{\bar{R}}\cdot\overrightarrow{EP}$

o, empleando coordenadas

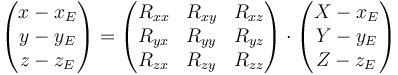
$\begin{pmatrix}x-x_E\\ y-y_E\\ z-z_E\end{pmatrix} = \begin{pmatrix}R_{xx}& R_{xy}&R_{xz}\\ R_{yx}&R_{yy}&R_{yz}\\ R_{zx}&R_{zy}&R_{zz}\end{pmatrix}\cdot\begin{pmatrix}X-x_E\\ Y-y_E\\ Z-z_E\end{pmatrix}$

o, equivalentemente

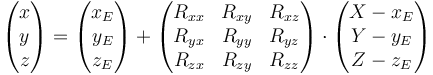
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}x_E\\ y_E\\ z_E\end{pmatrix}+\begin{pmatrix}R_{xx}& R_{xy}&R_{xz}\\ R_{yx}&R_{yy}&R_{yz}\\ R_{zx}&R_{zy}&R_{zz}\end{pmatrix}\cdot\begin{pmatrix}X-x_E\\ Y-y_E\\ Z-z_E\end{pmatrix}$

es decir,

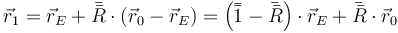
$\vec{r}_1 = \vec{r}_E+\bar{\bar{R}}\cdot(\vec{r}_0-\vec{r}_E)=\left(\bar{\bar{1}}-\bar{\bar{R}}\right)\cdot\vec{r}_E + \bar{\bar{R}}\cdot\vec{r}_0$

Al final, como siempre, el movimiento se reduce a una rotación seguida de una traslación.

Si ahora tenemos dos movimientos consecutivos, basta aplicar primero uno, para obtener un punto intermedio, y luego aplicar el segundo movimiento a éste.

Si la primera rotación es en torno al origen, el efecto de la segunda es

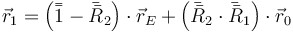
$\vec{r}_1 = \left(\bar{\bar{1}}-\bar{\bar{R}}_2\right)\cdot\vec{r}_E + \left(\bar{\bar{R}}_2\cdot\bar{\bar{R}}_1\right)\cdot\vec{r}_0$

Es decir, la rotación total es la composición de las dos

$\bar{\bar{R}}=\bar{\bar{R}}_2\cdot\bar{\bar{R}}_1$

y la traslación es

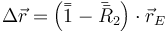
$\Delta\vec{r}=\left(\bar{\bar{1}}-\bar{\bar{R}}_2\right)\cdot\vec{r}_E$

3 Primer caso

Una rotación de un ángulo θ en torno al eje OY se realiza mediante la matriz

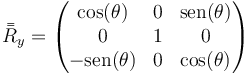
$\bar{\bar{R}}_y=\begin{pmatrix}\cos(\theta)& 0&\mathrm{sen}(\theta)\\ 0&1&0\\ -\mathrm{sen}(\theta)&0&\cos(\theta)\end{pmatrix}$

que para el caso de una rotación de +90&degree; se reduce a

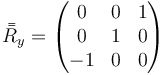
$\bar{\bar{R}}_y=\begin{pmatrix}0& 0&1\\ 0&1&0\\ -1&0&0\end{pmatrix}$

y para una de −90&degree;

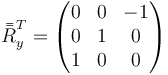
$\bar{\bar{R}}_y^T=\begin{pmatrix}0& 0&-1\\ 0&1&0\\ 1&0&0\end{pmatrix}$

Según esto, el resultado de la primera rotación es

$\begin{pmatrix}x_1\\ y_1\\ z_1\end{pmatrix} = \begin{pmatrix}0& 0&1\\ 0&1&0\\ -1&0&0\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix} =\begin{pmatrix}Z\\ Y\\ -X\end{pmatrix}$

El de la segunda, alrededor de un eje por (b,0,0) es

$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}0& 0&-1\\ 0&1&0\\ 1&0&0\end{pmatrix}\cdot\begin{pmatrix}Z-b\\ Y\\ -X\end{pmatrix} =\begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}X\\ Y\\ Z-b\end{pmatrix}=\begin{pmatrix}X+b\\ Y\\ Z-b\end{pmatrix}$

Por tanto, el resultado neto de los dos movimientos es

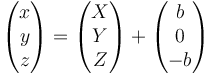
$\begin{pmatrix}x\\ y\\ z\end{pmatrix}=\begin{pmatrix}X\\ Y\\ Z\end{pmatrix}+\begin{pmatrix}b\\ 0\\ -b\end{pmatrix}$

es decir, una traslación,

$\vec{r}=\vec{r}_0+\Delta\vec{r}\qquad\qquad \Delta\vec{r}=b\vec{\imath}_1-b\vec{k}_1$

Directamente podemos verlo empleando las fórmulas del final del apartado anterior. La composición de rotaciones es

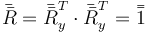
$\bar{\bar{R}}=\bar{\bar{R}}_y^T\cdot\bar{\bar{R}}_y^T = \bar{\bar{1}}$

resulta la unidad pues se anulan mutuamente.

La traslación es

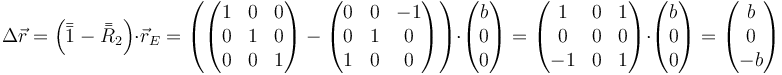
$\Delta\vec{r}=\left(\bar{\bar{1}}-\bar{\bar{R}}_2\right)\cdot\vec{r}_E= \left(\begin{pmatrix}1& 0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}-\begin{pmatrix}0& 0&-1\\ 0&1&0\\ 1&0&0\end{pmatrix}\right)\cdot\begin{pmatrix}b\\ 0\\ 0\end{pmatrix}=\begin{pmatrix}1& 0&1\\ 0&0&0\\ -1&0&1\end{pmatrix}\cdot\begin{pmatrix}b\\ 0\\ 0\end{pmatrix}=\begin{pmatrix}b\\ 0\\ -b\end{pmatrix}$

4 Segundo caso

En el segundo caso tenemos dos rotaciones en el mismo sentido. Al aplicar la primera rotación tenemos, como antes

$\begin{pmatrix}x_1\\ y_1\\ z_1\end{pmatrix} = \begin{pmatrix}0& 0&1\\ 0&1&0\\ -1&0&0\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix} =\begin{pmatrix}Z\\ Y\\ -X\end{pmatrix}$

y en la segunda

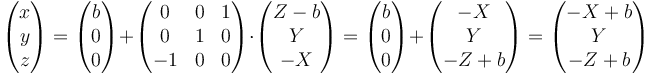
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}0& 0&1\\ 0&1&0\\ -1&0&0\end{pmatrix}\cdot\begin{pmatrix}Z-b\\ Y\\ -X\end{pmatrix} =\begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}-X\\ Y\\ -Z+b\end{pmatrix}=\begin{pmatrix}-X+b\\ Y\\ -Z+b\end{pmatrix}$

Si escribimos este resultado en forma matricial queda

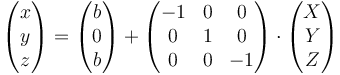
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}b\\ 0\\ b\end{pmatrix}+\begin{pmatrix}-1& 0&0\\ 0&1&0\\ 0&0&-1\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix}$

Esta matriz corresponde a un giro de 180° alrededor del eje OY seguida de una traslación

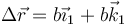
$\Delta \vec{r}=b\vec{\imath}_1+b\vec{k}_1$

El desplazamiento en la dirección del eje de giro (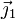 $\vec{\jmath}_1$ ) es

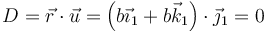
$D=\vec{r}\cdot\vec{u}=\left(b\vec{\imath}_1+b\vec{k}_1\right)\cdot\vec{\jmath}_1 = 0$

y por tanto el movimiento es una rotación pura. Es fácil comprobar que el punto $E ( - b / 2,0, - b / 2)$ es un punto fijo, no afectado por la transformación y, por tanto, por él pasa el eje.

5 Tercer caso

En el tercer caso, la segunda rotación es alrededor de un eje paralelo a OZ. En general, la matriz de rotación para este eje es

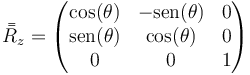
$\bar{\bar{R}}_z=\begin{pmatrix}\cos(\theta)& -\mathrm{sen}(\theta) & 0\\ \mathrm{sen}(\theta)&\cos(\theta)&0\\0&0&1 \end{pmatrix}$

que, para un ángulo de −90° queda

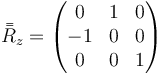
$\bar{\bar{R}}_z=\begin{pmatrix}0& 1 & 0\\ -1&0&0\\0&0&1 \end{pmatrix}$

En este caso, la primera rotación es la misma que en los dos casos anteriores

$\begin{pmatrix}x_1\\ y_1\\ z_1\end{pmatrix} = \begin{pmatrix}0& 0&1\\ 0&1&0\\ -1&0&0\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix} =\begin{pmatrix}Z\\ Y\\ -X\end{pmatrix}$

y en la segunda

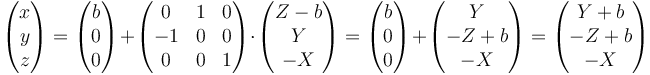
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}0& 1&0\\ -1&0&0\\ 0&0&1\end{pmatrix}\cdot\begin{pmatrix}Z-b\\ Y\\ -X\end{pmatrix} =\begin{pmatrix}b\\ 0\\ 0\end{pmatrix}+\begin{pmatrix}Y\\ -Z+b\\ -X\end{pmatrix}=\begin{pmatrix}Y+b\\ -Z+b\\ -X\end{pmatrix}$

Si escribimos este resultado en forma matricial queda

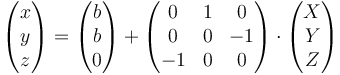
$\begin{pmatrix}x\\ y\\ z\end{pmatrix} = \begin{pmatrix}b\\ b\\ 0\end{pmatrix}+\begin{pmatrix}0& 1&0\\ 0&0&-1\\ -1&0&0\end{pmatrix}\cdot\begin{pmatrix}X\\ Y\\ Z\end{pmatrix}$

El eje de esta rotación lo da el autovector correspondiente al autovalor unidad, que en este caso es, una vez normalizado

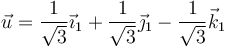
$\vec{u}=\frac{1}{\sqrt{3}}\vec{\imath}_1+\frac{1}{\sqrt{3}}\vec{\jmath}_1-\frac{1}{\sqrt{3}}\vec{k}_1$

El desplazamiento en la dirección del eje es

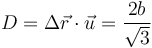
$D=\Delta\vec{r}\cdot\vec{u}=\frac{2b}{\sqrt{3}}$

Al no ser nulo, el movimiento es helicoidal.

Composición de dos rotaciones de 90° (CMR)

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Primer caso

4 Segundo caso

5 Tercer caso

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES