De Laplace

1 Enunciado

Dos coches ruedan por un tramo recto de autopista con la misma velocidad $v 0$ y separados por una distancia $d 0$ . En un instante dado, el coche que va delante frena con aceleración uniforme de módulo $a 0$ hasta quedar parado. El coche que va detrás tarda un tiempo $t f$ en empezar a frenar con la misma aceleración que el primero.

Determina como cambia la distancia entre los coches con el tiempo.
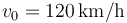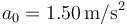Si $t_f=0.30\,\mathrm{s}$ , $v_0=120\,\mathrm{km/h}$ y $a_0=1.50\,\mathrm{m/s^2}$ , calcula el valor mínimo de $d 0$ para que los coches no colisionen.

2 Solución

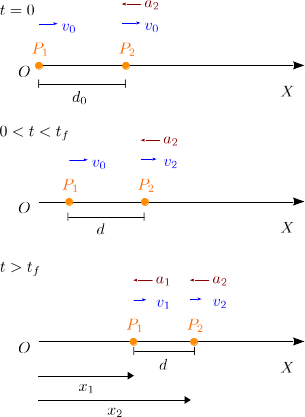
El esquema mostrado a la derecha resume la situación descrita en el problema. En el instante inicial los dos coches tienen la misma velocidad y están separados una distancia $d 0$ . En ese instante el coche que va delante (representado por $P 2$ ) empieza a frenar con aceleración constante $a 0$ . El coche que va detras ( $P 1$ ) sigue moviéndose con velocidad constante hasta el instante $t = t f$ . A partir de ese instante empieza a frenar con la misma aceleración que el 2.

Escogemos como eje $X$ la recta sobre la que se mueven los coches. Colocamos el origen en la posición del coche 1 en el instante incial. El coche 2 se mueve siempre con aceleración $- a 0$ , su velocidad inicial es $v 0$ y su posición inicial es $d 0$ . Como realiza un movimiento rectilíneo uniformemente acelerado se tiene

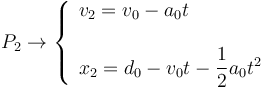
$P_2 \to \left\{ \begin{array}{l} v_2 = v_0 - a_0 t\\ \\ x_2 = d_0 - v_0t - \dfrac{1}{2}a_0 t^2 \end{array} \right.$

Para el coche 1 hay que considerar dos intervalos de tiempo, $0 < t < t f$ y $t > t f$ . En el primero realiza un movimiento rectilíneo uniforme y en el segundo un movimiento rectilíneo uniformemente acelerado. Tenemos

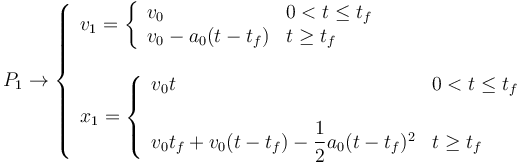
$P_1 \to \left\{ \begin{array}{l} v_1 = \left\{ \begin{array}{ll} v_0 & 0<t\leq t_f\\ v_0 - a_0(t-t_f) & t\geq t_f \end{array} \right. \\ \\ x_1 = \left\{ \begin{array}{ll} v_0t & 0<t\leq t_f\\ \\ v_0t_f + v_0(t-t_f) - \dfrac{1}{2}a_0(t-t_f)^2 & t\geq t_f \end{array} \right. \end{array} \right.$

En $t = t f$ el coche 1 se encuentra en la coordenada $v 0 t f$ y tiene velocidad $v 0$ . Este valor de tiempo es el instante inicial para el movimiento en el segundo intervalo de tiempo. Por eso en las fórmulas de movimiento uniformemente acelerado ponemos $t - t f$ en vez de $t f$ .

Como se ve en el esquema la distancia entre los dos coches es

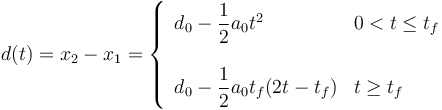
$d(t) = x_2 - x_1 = \left\{ \begin{array}{ll} d_0 - \dfrac{1}{2}a_0t^2 & 0<t\leq t_f\\ \\ d_0 - \dfrac{1}{2}a_0t_f(2t-t_f) & t\geq t_f \end{array} \right.$

Para cada intervalo hemos usado la expresión correspondiente de $x 1$ . La de $x 2$ es la misma para todo tiempo. Se puede comprobar que si ponemos $t = t f$ en las expresiones anteriores los dos valores coinciden, como debe ser.

El instante de tiempo en que se para el coche 2 es

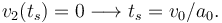
$v_2(t_s) = 0 \longrightarrow t_s = v_0/a_0.$

El coche 1 empieza a frenar después de que el otro frene. Para que los dos coches no colisionen es necesario que en $t = t s$ la distancia entre ellos sea mayor que cero. Escogiendo la expresión de $d (t)$ para $t > t s$ tenemos

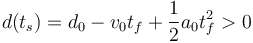
$d(t_s) = d_0 - v_0t_f + \dfrac{1}{2}a_0t_f^2>0$

Pasando los dos últimos sumando a la derecha obtenemos la condición

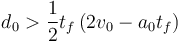
$d_0 > \dfrac{1}{2}t_f\,(2v_0-a_0t_f)$

Usando los valores numéricos del apartado b obtenemos

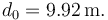
$d_0 = 9.92 \,\mathrm{m}.$

Esta distancia corresponde a la longitud de dos coches, aproximadamente.

2.1 Comentario

Si el valor de $d 0$ es lo bastante pequeño puede ocurrir que el coche 1 choque con el 2 antes de que empiece a frenar, es decir, en el intervalo $t < t f$ . Para que esto no ocurra debe cumplirse

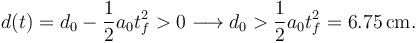
$d(t) = d_0 - \dfrac{1}{2}a_0t_f^2 > 0 \longrightarrow d_0 > \dfrac{1}{2}a_0t_f^2 = 6.75\,\mathrm{cm}.$

Hemos usado la expresión de $d (t)$ para el intervalo de tiempo $t < t f$ y los valores numéricos del apartado b.

Coches frenando en una autopista

De Laplace

1 Enunciado

2 Solución

2.1 Comentario

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES