Circulación por un terreno ondulado

De Laplace

1 Enunciado

En un tramo ondulado de una autopista, el perfil de esta puede modelarse como una sinusoide

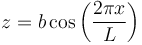
$z=b\cos\left(\frac{2\pi x}{L}\right)$

¿Cuál es la máxima rapidez que puede llevar un coche de masa m si no debe despegar del suelo al pasar por una de las crestas?
Si el coche continúa con esta rapidez, ¿cuánto vale la reacción del suelo cuando pasa por el fondo de un valle?

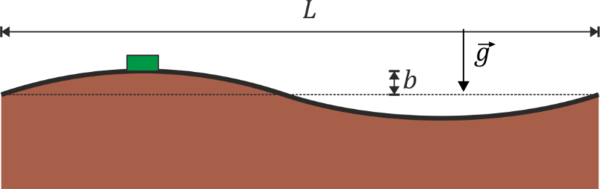
2 Rapidez máxima

Podemos resolver para un perfil arbitrario y luego particularizar para el que nos dan.

La posición del vehículo en cada instante se puede poner, en forma vectorial como

$\vec{r}=x\vec{\imath}+z(x)\vec{k}$

La velocidad en cada instante la obtenemos por la regla de la cadena

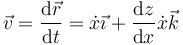
$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=\dot{x}\vec{\imath}+\frac{\mathrm{d}z}{\mathrm{d}x}\dot{x}\vec{k}$

Derivando de nuevo hallamos la aceleración

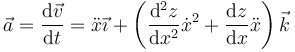
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\ddot{x}\vec{\imath}+\left(\frac{\mathrm{d}^2z}{\mathrm{d}x^2}\dot{x}^2+\frac{\mathrm{d}z}{\mathrm{d}x}\ddot{x}\right)\vec{k}$

En la cima de la cresta, la altura es máxima, por lo que

$z=z_\mathrm{max}\qquad\Rightarrow\qquad \frac{\mathrm{d}z}{\mathrm{d}x}=0$

lo que da la velocidad horizontal

$(z=z_\mathrm{max})\qquad \qquad\vec{v}=\dot{x}\vec{\imath}$

y la aceleración

$(z=z_\mathrm{max})\qquad \qquad\vec{a}=\ddot{x}\vec{\imath}+\frac{\mathrm{d}^2z}{\mathrm{d}x^2}\dot{x}^2\vec{k}$

Dada la dirección de la velocidad, la componente horizontal de la aceleración es la aceleración tangencial y la vertical es la aceleración normal.

Justo en la cresta, la componente vertical de la segunda ley de Newton nos da

$ma_z = F_n-mg\qquad\Rightarrow\qquad F_n= m(g+a_z)$

Sustituimos la expresión anterior

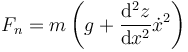
$F_n = m\left(g+\frac{\mathrm{d}^2z}{\mathrm{d}x^2}\dot{x}^2\right)$

En un máximo la segunda derivada es negativa, por lo que esta fuerza es menor que el peso. La rapidez máxima la obtenemos viendo para que valor esta fuerza se anula, por tratarse de un vínculo unilateral. Una rapidez mayor nos daría una fuerza normal negativa, lo cual no es posible (el suelo no tira del vehículo). Esto nos da la condición

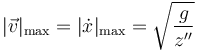
$|\vec{v}|_\mathrm{max}=|\dot{x}|_\mathrm{max}=\sqrt{\frac{g}{z''}}$

con z" la segunda derivada de z con respecto a x, evaluada en la posición del máximo.

En el caso particular de la sinusoide el máximo se da en x = 0

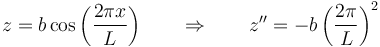
$z = b\cos\left(\frac{2\pi x}{L}\right)\qquad\Rightarrow\qquad z''=-b\left(\frac{2\pi}{L}\right)^2$

lo que nos da la rapidez máxima

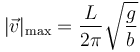
$|\vec{v}|_\mathrm{max}=\frac{L}{2\pi}\sqrt{\frac{g}{b}}$

3 Fuerza en el valle

Aplicando el mismo razonamiento, la fuerza en el mínimo del perfil será

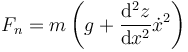
$F_n = m\left(g+\frac{\mathrm{d}^2z}{\mathrm{d}x^2}\dot{x}^2\right)$

donde ahora la segunda derivada es postiva y la fuerza normal es superior al peso.

Si la rapidez es constante y la curva es simétrica (como ocurre en el coseno) el segundo sumando vale exactamente +mg (ya que en el máximo vale −mg). Por tanto, el valle

$(z=z_\mathrm{min})\qquad \qquad F_n = 2mg$

Circulación por un terreno ondulado

De Laplace

1 Enunciado

2 Rapidez máxima

3 Fuerza en el valle

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES