Circuito alrededor de un solenoide (GIOI)

De Laplace

1 Enunciado

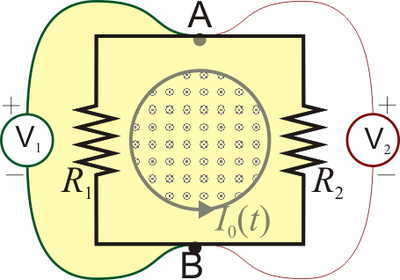
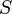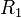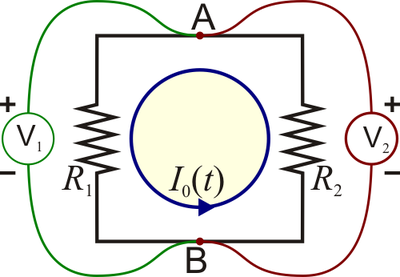
Se tiene un solenoide largo de sección , y densidad de espiras n por el cual circula una corriente variable en el tiempo I₀(t). Dos voltímetros miden el voltaje entre dos puntos y , diametralmente opuestos, de un circuito formado por dos resistencias y 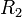, tal como se ve en la figura. Halle las lecturas de los voltímetros. ¿Coincidirán éstas? ¿Por qué?

2 Corriente que fluye por el circuito

Este problema es una aplicación inmediata de la ley de Faraday, si bien su apariencia es un tanto engañosa. Tenemos un circuito formado por dos resistencias y, aparentemente, sin generador. Éste es el solenoide central, en cuyo interior hay un campo magnético variable. El flujo de este campo a través de una superficie limitada por el circuito no es nulo, aunque no haya campo magnético en ningún punto del circuito.

Tenemos que

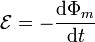
La fuerza electromotriz, al estar el circuito en reposo, coincide con la circulación del campo eléctrico

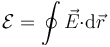
Vemos que el campo eléctrico, en este caso, no es conservativo. Esta integral se puede descomponer en dos tramos, uno por cada resistencia, en cada uno de los cuales, el campo eléctrico es proporcional a la densidad de corriente.

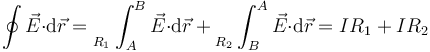
Por su parte, el flujo magnético es

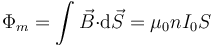
ya que, en el interior de un solenoide largo y con el sentido de la corriente indicado en la figura, 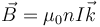. Obsérvese que la sección es la del solenoide, no la de una superficie apoyada en la espira formada por las dos resistencias, ya que el campo es no nulo sólo dentro del solenoide.

Según esto

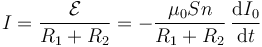
Ésta es la corriente que circula por el circuito.

3 Lectura del voltímetro V₁

La tensión que mide el voltímetro V₁ coincide con la caída de tensión en la resistencia R₁, pero no con la que hay en la resistencia R₂. La razón es que un voltímetro determina la integral del campo eléctrico a través de un camino que pasa por su interior. Para que este coincida con la integral a través de una resistencia debe ocurrir, de nuevo según la ley de Faraday, que no haya variación de flujo magnético entre ambos caminos.

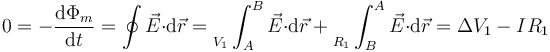
Resulta entonces

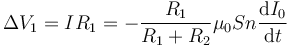
4 Lectura del voltímetro V₂

Análogamente, en el voltímetro V₂ se obtiene la caída de tensión en la resistencia R₂ (teniendo en cuenta el sentido de la corriente). Integrando a lo largo del contorno que pasa por R₂ y V₂

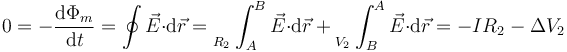
La integral a lo largo de R₂ da − IR₂ porque la estamos recorriendo en el sentido contrario al del primer apartado, cuando definimos el sentido de I.

De la expresión anterior

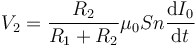
Éste es un ejemplo de cómo el potencial eléctrico no está definido, en general, cuando hay campos variables en el tiempo, y de como el voltaje depende del camino. O, dicho de otro modo, que la lectura del voltímetro puede depender de cómo esté situado el aparato.

¿Cómo hubieran sido los cálculos si hubiéramos tomado un camino que pasara por el voltímetro V₁ y la resistencia R₂? ¿Hubiera resultado que el voltímetro V₁ mediría el voltaje en la resistencia R₂?

No, puesto que entonces el flujo magnético a través de una superficie apoyada en este contorno no sería cero, sino que incluiría la contribución del solenoide central, de modo que

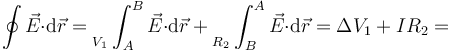
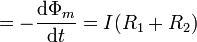
de donde de nuevo obtenemos que

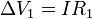
como era de esperar, ya que la lectura del voltímetro refleja lo que sucede dentro del propio voltímetro, y no de como se nos ocurra cerrar el camino de integración.