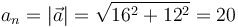Caso de oscilador armónico tridimensional(GIE)

De Laplace

1 Enunciado

Una partícula se mueve de manera que su posición en todo momento se expresa, en las unidades fundamentales del SI, como

$\vec{r}=4\cos⁡(2t)\vec{\imath}+4\,\mathrm{sen}⁡(2t)\vec{\jmath}+3\cos⁡(2t)\vec{k}$

Para este movimiento…

Demuestre que:
1. Se trata de un movimiento plano. Halle un vector unitario ortogonal al plano del movimiento.
2. Cumple la ecuación del oscilador armónico en tres dimensiones. ¿Qué tipo de curva es la trayectoria que sigue la partícula?
¿Entre qué valores se encuentra la distancia de la partícula al origen de coordenadas? ¿Entre qué valores se halla la rapidez de la partícula?
Exprese la posición, velocidad y aceleración de este movimiento en todo instante empleando las coordenadas cilíndricas y la base asociada a ellas.
Para el instante , halle
1. La posición, velocidad y aceleración de la partícula.
2. El triedro de Frenet referido a la base canónica $\{\vec{\imath},\vec{\jmath},\vec{k}\}$
3. Las componentes intrínsecas de la aceleración (escalares).

2 Demostraciones

En lo que sigue todas las cantidades con dimensiones están en las unidades fundamentales del SI: m, s o combinaciones de estos.

2.1 Movimiento plano

El vector de posición se puede escribir en la forma

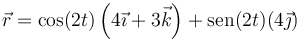
$\vec{r}=\cos(2t)\left(4\vec{\imath}+3\vec{k}\right)+\mathrm{sen}(2t)(4\vec{\jmath})$

que es de la forma

$\vec{r}=f(t)\vec{A}+g(t)\vec{C}$

y por tanto el movimiento es plano.

Un vector ortogonal lo hallamos como el producto vectorial de los dos que definen el plano

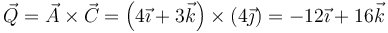
$\vec{Q}=\vec{A}\times\vec{C}=\left(4\vec{\imath}+3\vec{k}\right)\times(4\vec{\jmath})=-12\vec{\imath}+16\vec{k}$

Hallamos el unitario dividiendo por su módulo

$\vec{B}=\frac{\vec{Q}}{|\vec{Q}|}=-\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{k}$

también puede hallarse este vector como el binormal del triedro de Frenet, que se calcula más adelante.

2.2 Oscilador armónico

Derivando una vez respecto al tiempo obtenemos la velocidad

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-8\,\mathrm{sen}⁡(2t)\vec{\imath}+8\,\mathrm{cos}⁡(2t)\vec{\jmath}-6\,\mathrm{sen}⁡(2t)\vec{k}$

y derivando una segunda la aceleración

$\vec{r}=-16\cos⁡(2t)\vec{\imath}-16\,\mathrm{sen}⁡(2t)\vec{\jmath}-12\cos⁡(2t)\vec{k}$

Esta aceleración cumple

$\vec{a}=-4\vec{r}$

que es la ecuación del oscilador armónico con $ω = 2$ .

Como consecuencia, el movimiento es plano, como ya sabíamos, y la forma de la curva es una elipse.

3 Cotas de distancia y velocidad

3.1 Distancia al origen

La distancia al origen la da el módulo del vector de posición

$|\vec{r}|=\sqrt{x^2+y^2+z^2}=\sqrt{16\cos^2(2t)+16\,\mathrm{sen}^2(2t)+9\cos^2(2t)}$

Simplificada da

$|\vec{r}|=\sqrt{16+9\,\mathrm{cos}^2(2t)}$

El coseno al cuadrado varía entre 0 y 1. Por tanto

$|\vec{r}|_\mathrm{min}=\sqrt{16}=4\qquad\qquad |\vec{r}|_\mathrm{max}=\sqrt{16+9}=5$

3.2 Rapidez

Operamos de la misma manera con el módulo de la velocidad

$\vec{v}=\frac{\mathrm{d}\vec{r}}{\mathrm{d}t}=-8\,\mathrm{sen}⁡(2t)\vec{\imath}+8\,\mathrm{cos}⁡(2t)\vec{\jmath}-6\,\mathrm{sen}⁡(2t)\vec{k}$

y da

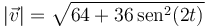
$|\vec{v}|=\sqrt{64+36\,\mathrm{sen}^2(2t)}$

que por la misma razón tiene valores mínimo y máximo

$|\vec{v}|_\mathrm{min}=\sqrt{64}=8\qquad\qquad |\vec{r}|_\mathrm{max}=\sqrt{64+36}=10$

Los máximos y mínimos de la distancia y la rapidez van alternados. Donde la distancia es máxima, la rapidez es mínima y viceversa.

4 Expresión en cilíndricas

4.1 Coordenadas

Pasando de cartesianas

$x = 4\cos(2t)\qquad\qquad y = 4\,\mathrm{sen}(2t)\qquad\qquad z = 3\cos(2t)$

a cilíndricas queda

$\rho = \sqrt{x^2+y^2}=4\qquad \theta=\mathrm{arctg}\left(\frac{y}{x}\right)=2t\qquad\qquad z=3\cos(2t)$

Siendo sus primeras derivadas temporales

$\dot{\rho} = 0\qquad \dot{\theta}=2\qquad\qquad \dot{z}=-6\,\mathrm{sen}(2t)$

y las segundas

$\ddot{\rho} = 0\qquad \ddot{\theta}=0\qquad\qquad \dot{z}=-12\,\mathrm{cos}(2t)$

4.2 Vector de posición

Es

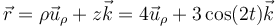
$\vec{r}=\rho\vec{u}_\rho+z\vec{k}=4\vec{u}_\rho+3\cos(2t)\vec{k}$

4.3 Velocidad

Sustituimos

$\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta+\dot{z}\vec{k}=8\vec{u}_\theta-6\,\mathrm{sen}(2t)\vec{k}$

4.4 Aceleración

Queda

$\vec{a}=(\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho+(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{u}_\theta+\ddot{z}\vec{k}=-16\vec{u}_\rho-12\,\mathrm{cos}(2t)\vec{k}$

5 Estado en un instante

5.1 Posición, velocidad y aceleración

Hacemos t=0 en la posición

$\vec{r}(t=0)=4\vec{\imath}+3\vec{k}$

velocidad

$\vec{v}(t=0)=8\vec{\jmath}$

y aceleración

$\vec{a}(t=0)=-16\vec{\imath}-12\vec{k}$

5.2 Triedro de Frenet

5.2.1 Vector tangente

Es el unitario en la dirección y sentido de la velocidad

$\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\vec{\jmath}$

5.2.2 Vector binormal

Es el ortogonal a la velocidad y la aceleración

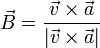
$\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}$

lo que da

$\vec{v}\times\vec{a}=8\vec{\jmath}\times(-16\vec{\imath}-12\vec{k})= -96\vec{\imath}+128\vec{k}\qquad \qquad |\vec{v}\times\vec{a}|=160$

y resulta

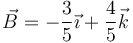
$\vec{B}=-\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{k}$

5.2.3 Vector normal

Se obtiene de los dos anteriores (no es la única forma; también puede normalizarse la aceleración normal)

$\vec{N}=\vec{B}\times\vec{T}=-\frac{4}{5}\vec{\imath}-\frac{3}{5}\vec{k}$

5.3 Componentes intrínsecas de la aceleración

5.3.1 Aceleración tangencial

Es nula, por ser la aceleración ortogonal a la velocidad

$a_t=\vec{a}\cdot\vec{T}=(-16\vec{\imath}-12\vec{k})\cdot\vec{\jmath}=0$

5.3.2 Aceleración normal

Como es nula la tangencial, toda la aceleración es normal y

$a_n=|\vec{a}|=\sqrt{16^2+12^2}= 20$

Caso de oscilador armónico tridimensional(GIE)

De Laplace

Contenido