Cargas en un triángulo Primera Prueba de Control 2010/11 (F2GIA)
De Laplace
Contenido |
1 Enunciado
Tenemos un triángulo equilátero de lado 
. En los vértices de la base se disponen dos cargas puntuales − q y + q con 
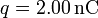. La constante de Coulomb es 
.
El módulo del campo eléctrico en el vértice superior del triángulo es
.
.
.
.
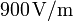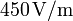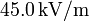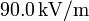Se coloca un dipolo eléctrico en él vértice superior de módulo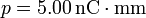 
formando un ángulo 
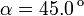con el eje X. El par que ejerce el campo sobre el dipolo es
-
.
-
.
-
.
-
.
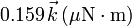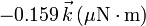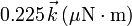2 Solución
2.1 Campo eléctrico en el vértice
La respuesta correcta es la 3.
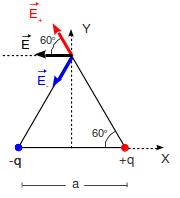
El campo en el vértice superior es la suma vectorial del campo generado por las dos cargas en los vértices de la base. Como se indica en la figura, el campo creado por la carga positiva se aleja de ésta, mientras que el creado por la carga negativa se dirige hacia ella. Al hacer la suma vectorial se cancelan las componentes en el eje Y y se suman las componentes en el eje X, apuntando hacia el sentido negativo.
El módulo de ambos campos es el mismo, pues las dos cargas son iguales en magnitud y están a la misma distancia. Tenemos
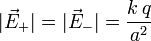
El ángulo sobre el que hay que proyectar los campos es 60o. Así pues el campo total es
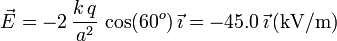
Y el módulo del campo es
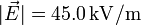
Los errores típicos en este apartado son hacer la suma de los módulos sin tener en cuenta que es una suma vectorial y utilizar mal las unidades.
2.2 Par sobre el dipolo
La respuesta correcta es la 1.
El par de fuerzas que un campo eléctrico ejerce sobre un dipolo viene dado por la expresión
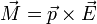
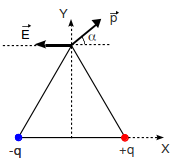
En nuestro caso es dipolo es
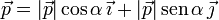
Al hacer el producto vectorial con el campo del apartado anterior obtenemos
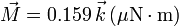
En el dibujo se observa que al hacer el producto vectorial hay que girar el vector 
sobre el vector <math\vec{E}> </math>. Por tanto, el par debe apuntar en la dirección positiva del eje Z.
