Cambios de presión, volumen y temperatura en gas ideal (F2GIA)

De Laplace

1 Enunciado

Cierto gas ideal constituye un sistema termodinámico (supuestamente cerrado) que evoluciona desde un estado inicial a otro final. Tras el proceso, se comprueba que tanto su presión como su volumen han disminuido, mientras que su temperatura ha sufrido un aumento. ¿Qué conclusión podemos extraer?

2 Solución

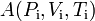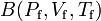Consideremos que los estados inicial y final del sistema están caracterizados por sendas ternas de valores de coordenadas termodinámicas, y , respectivamente. Independientemente del proceso seguido, si el sistema es un gas que verifica las condiciones del gas ideal, en ambos estados se deberá verificar la ecuación de estado,

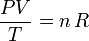
donde 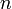representa la cantidad de gas, y R la constante de los gases ideales: si 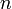está expresado en moles de sustancia, dicha constante universal vale, aproximadamente, 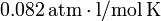, equivalente a unas .

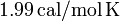Por otra parte, si los valores iniciales y finales de presión, volumen y temperatura verifican las relaciones...

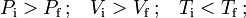
... las cantidades de gas, inicial 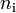, y final 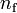, deben ser tales que...

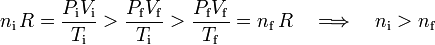
Es decir, para que en el proceso disminuyan la presión y el volumen del gas, a la vez que aumente su temperatura, es necesario que la cantidad de gas final sea estrictamente menor que la inicial. En consecuencia, el sistema no puede ser cerrado: debe existir algún tipo de fuga, pues son incompatibles los cambios en las coordenadas termodinámicas con que la cantidad de gas permanezca constante.