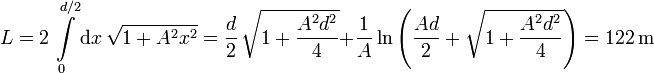Cable soportando una tubería sobre un río

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Tensión máxima
- 2.2 Longitud del cable

1 Enunciado

Unos ingenieros utilizan un cable para suspender una tubería sobre un río. La distancia entre las torres es de 120 m y la flecha del cable es de 10.0 m. El peso total de la tubería suspendida es de 6000 kg. El peso del propio cable es despreciable.

Calcula la tensión máxima en el cable suspendido.
Calcula la longitud del cable suspendido

2 Solución

2.1 Tensión máxima

Un cable sometido a una carga distribuida uniformemente a lo largo de una horizontal adopta la forma de una parábola. En este caso los anclajes están a la misma altura, por lo que sólo hay una flecha.

La parábola viene descrita por la expresión

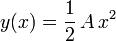
$y(x) = \dfrac{1}{2}\,A\,x^2$

donde se toma como origen el punto más bajo del cable. La constante $A$ es

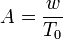
$A = \dfrac{w}{T_0}$

donde $w$ es el peso por unidad de longitud de la carga y $T 0$ es la tensión del cable en el punto más bajo.

En este caso los dos anclajes están a la misma altura, es decir, sólo hay una flecha $h$ . Entonces el punto más bajo es equidistante de los anclajes. Si la cuerda es $d$ , en el anclaje de la derecha tenemos

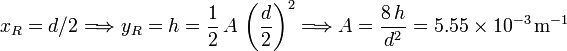
$x_R = d/2 \Longrightarrow y_R = h = \dfrac{1}{2}\,A\,\left(\dfrac{d}{2}\right)^2 \Longrightarrow A = \dfrac{8\,h}{d^2} = 5.55\times10^{-3}\,\mathrm{m^{-1}}$

Si el tablero tiene una masa $M$ , el peso por unidad de longitud es

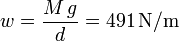
$w = \dfrac{M\,g}{d} = 491\,\mathrm{N/m}$

Entonces la tensión en el punto más bajo del cable es

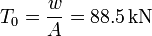
$T_0 = \dfrac{w}{A} = 88.5\,\mathrm{kN}$

La tensión varía con la distancia horizontal al punto más bajo según la expresión

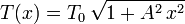
$T(x) = T_0\,\sqrt{1+A^2\,x^2}$

La tensión es máxima en el punto más alejado del punto más bajo. Cuando hay una sola flecha, la tensión es la misma en los dos anclajes y vale

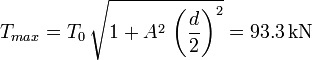
$T_{max} = T_0\,\sqrt{1+A^2\,\left(\dfrac{d}{2}\right)^2} = 93.3\,\mathrm{kN}$

2.2 Longitud del cable

La longitud de un elemento de cable es

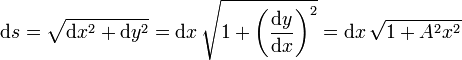
$\mathrm{d}s = \sqrt{\mathrm{d}x^2+\mathrm{d}y^2} = \mathrm{d}x\,\sqrt{1+\left(\dfrac{\mathrm{d}y}{\mathrm{d}x}\right)^2} = \mathrm{d}x\,\sqrt{1+A^2x^2}$

Integrando esta expresión se obtiene la longitud del cable. Cuando sólo hay una flecha podemos integrar desde el centro hacia uno de loa anclajes y multiplicar el resultado por dos. Tenemos en este caso

$L = 2\,\int\limits_{0}^{d/2}\mathrm{d}x\,\sqrt{1+A^2x^2} = \dfrac{d}{2}\,\sqrt{1+\dfrac{A^2d^2}{4}} + \dfrac{1}{A}\ln\left(\dfrac{Ad}{2}+ \sqrt{1+\dfrac{A^2d^2}{4}}\right)= 122\,\mathrm{m}$

Cable soportando una tubería sobre un río

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Tensión máxima

2.2 Longitud del cable

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES