Bola colgando de un muelle y un hilo, Noviembre 2011 (G.I.A.)

De Laplace

1 Enunciado

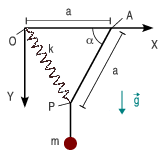
El sistema de la figura consta de una partícula de masa m, un muelle de constane elástica k y elongación natural nula, y una cuerda de longitud a. El punto de anclaje del muelle y de sujección de la cuerda están separados por una distancia a.

1. Determina la expresión que da la elongación del muelle en función del ángulo α y la longitud a.
2. Encuentra el valor del ángulo α en la posición de equilibrio.

2 Solución

2.1 Elongación del muelle

Aplicamos el teorema del coseno al triángulo OPA. La longitud de los lados AO y AP es a, y el ángulo entre ellos es α. Llamando l a la elongación del muelle (lado OP) tenemos

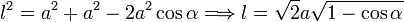
2.2 Valor de equilibrio del ángulo

Las fuerza que actúan en el punto P son el peso de la masa m 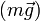, la fuerza del muelle 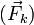y la tensión del hilo PA 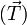. La suma de las tres fuerzas tiene que anularse. En el sistema de ejes de la figura estas fuerzas son

La condición de equilibrio es

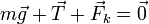
Igualando componente a componente tenemos

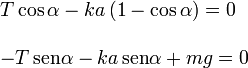
Para encontrar la expresión del ángulo multiplicamos la primera ecuación por 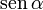, la segunda por cosα y las sumamos. Con eso se obtiene

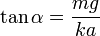
Podemos observar que si el muelle es muy fuerte (k muy grande), el ángulo tiende a cero, lo cual es razonable.