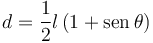Barra conectada a un deslizador, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

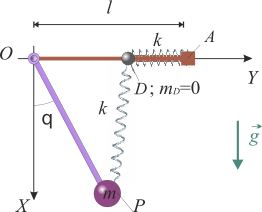
Un cuerpo pesado de masa $m$ , que puede considerarse como una partícula material $P$ , está unido a un extremo de una barra de longitud $l$ y masa despreciable que tiene su otro extremo articulado en un punto fijo $O$ . Partícula y barra están obligadas a permanecer en el plano vertical $O X Y$ , tal que el eje $O X$ coincide con la dirección y el sentido de la acción de la gravedad. Además, hay un deslizador puntual $D$ , de masa despreciable que puede moverse insertado en otra barra fija horizontal $O A$ , también de longitud $l$ y coincidente con el eje $O X$ . Dos resortes idénticos de longitud natural nula y constante recuperadora $k$ conectan dicho deslizador con la partícula $P$ y con el extremo $A$ de la barra horizontal fija. En primera aproximación, puede despreciarse el rozamiento entre el deslizador $D$ y la barra $O A$ .

Determine la posición del deslizador en función del angulo $θ$ que forma la barra $O P$ con la vertical gravitatoria, y obtenga la expresión de las fuerzas reales y vinculares que actúan sobre la partícula $P$ en función de dicho angulo.
¿Qué relación deben verificar los par ́metros $k$ , $l$ y $m$ para que el sistema se encuentre en equilibrio en la posición dada por $θ = π / 6$ ?
Si se considera que entre el deslizador y la barra existe rozamiento, caracterizado por un coeficiente de valor conocido $μ$ , determine las expresiones matemáticas (inecuaciones) que establecen el rango de las posiciones de equilibrio del sistema.
Obtenga las expresiones de las energías cinética y potencial de $P$ en función de la variable geométrica $θ$ y su derivada temporal.

2 Solución

2.1 Fuerzas sobre $P$

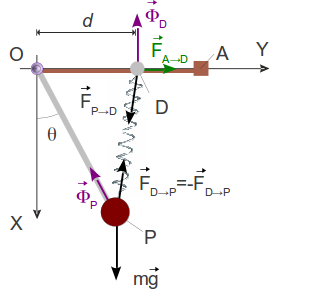
Las fuerzas que actúan sobre la partícula $P$ son la gravedad, la fuerza del muelle que la conecta con el deslizador y la fuerza de reacción vincular de la barra. La expresión de cada una de ellas en el sistema de ejes de la figura es

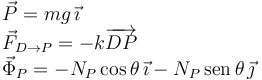
$\begin{array}{l} \vec{P} = mg\,\vec{\imath}\\ \vec{F}_{D\to P} = -k\overrightarrow{DP}\\ \vec{\Phi}_P = -N_P\cos\theta\,\vec{\imath} - N_P\,\mathrm{sen}\,\theta\,\vec{\jmath} \end{array}$

Tenemos que saber la posición del deslizador $D$ para poder expresar la fuerza del muelle. Este deslizador está sometido a tres fuerzas, a saber: la que ejerce el muelle que lo une con $P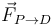$ ( $\vec{F}_{P\to D}$ ), la que ejerce el muelle que lo une con el punto $A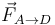$ ( $\vec{F}_{A\to D}$ ) y la fuerza de reacción vincular de la barra sobre la que desliza. Estas tres fuerzas son

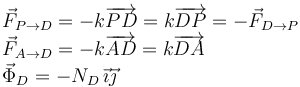
$\begin{array}{l} \vec{F}_{P\to D} = -k\overrightarrow{PD} = k\overrightarrow{DP} = -\vec{F}_{D\to P}\\ \vec{F}_{A\to D} = -k\overrightarrow{AD} = k\overrightarrow{DA} \\ \vec{\Phi}_D = -N_D\,\vec{\imath}\vec{\jmath} \end{array}$

Aplicando la segunda ley de Newton al deslizador tenemos

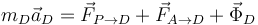
$m_D\vec{a}_D = \vec{F}_{P\to D} + \vec{F}_{A\to D} + \vec{\Phi}_D$

Pero la masa del deslizador es cero, por lo que la suma de estas tres fuerzas debe anularse

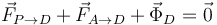
$\vec{F}_{P\to D} + \vec{F}_{A\to D} + \vec{\Phi}_D = \vec{0}$

Tenemos que expresar los vectores geométricos que aparecen en las fuerzas. Tenemos

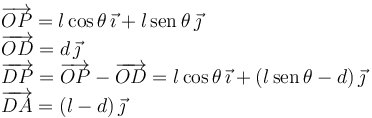
$\begin{array}{l} \overrightarrow{OP} = l\cos\theta\,\vec{\imath} + l\,\mathrm{sen}\,\theta\,\vec{\jmath}\\ \overrightarrow{OD} = d\,\vec{\jmath}\\ \overrightarrow{DP} = \overrightarrow{OP} - \overrightarrow{OD} = l\cos\theta\,\vec{\imath} + (l\,\mathrm{sen}\,\theta-d)\,\vec{\jmath}\\ \overrightarrow{DA} = (l-d)\,\vec{\jmath} \end{array}$

Usando que la suma de fuerzas sobre $D$ debe ser cero obtenemos

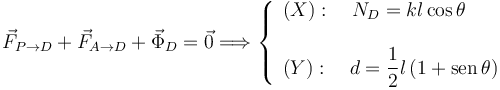
$\vec{F}_{P\to D} + \vec{F}_{A\to D} + \vec{\Phi}_D = \vec{0} \Longrightarrow \left\{ \begin{array}{l} (X): \quad N_D = kl\cos\theta\\ \\ (Y): \quad d = \dfrac{1}{2}l\,(1+\mathrm{sen}\,\theta) \end{array} \right.$

Es decir, la posición del deslizador viene dada por el vector

$\overrightarrow{OD} = \dfrac{1}{2}l\,(1+\mathrm{sen}\,\theta)\,\vec{\jmath}$

2.2 Equilibrio para 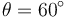$\theta=60^{\circ}$

La condición de equilibrio es que la suma de fuerzas sobre la partícula $P$ sea cero. Es decir

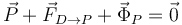
$\vec{P} + \vec{F}_{D\to P} + \vec{\Phi}_P = \vec{0}$

Del apartado anterior tenemos las expresiones de estas fuerzas

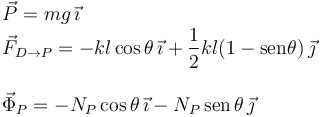
$\begin{array}{l} \vec{P} = mg\,\vec{\imath}\\ \vec{F}_{D\to P} = -kl\cos\theta\,\vec{\imath} + \dfrac{1}{2}kl(1-\mathrm{sen}\theta)\,\vec{\jmath} \\ \\ \vec{\Phi}_P = -N_P\cos\theta\,\vec{\imath} - N_P\,\mathrm{sen}\,\theta\,\vec{\jmath} \end{array}$

Ambas componentes de la ecuación vectorial deben anularse:

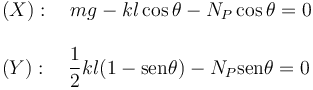
$\begin{array}{l} (X):\quad mg-kl\cos\theta - N_P\cos\theta = 0\\ \\ (Y):\quad \dfrac{1}{2}kl(1-\mathrm{sen}\theta) - N_P\mathrm{sen}\theta=0 \end{array}$

Para eliminar $N P$ multiplicamos la primera ecuación por $senθ$ , la segunda por $cosθ$ y las restamos. Obtenemos la relación

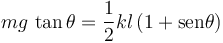
$mg\,\tan\theta = \dfrac{1}{2}kl\,(1+\mathrm{sen}\theta)$

Cuando 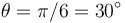$\theta=\pi/6=30^{\circ}$ tenemos

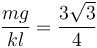
$\dfrac{mg}{kl} = \dfrac{3\sqrt{3}}{4}$

2.3 Análisis con rozamiento

Si hay rozamiento entre el deslizador y la barra, aparece una nueva fuerza sobre el deslizador paralela a la barra. Ahora no hay una sola posición de equilibrio para el deslizador. Si el coeficiente de rozamiento es lo bastante grande todas las posiciones pueden ser de equilibrio. La condición para que haya equilibrio es que el módulo de la fuerza de rozamiento sobre el deslizador sea menor que su valor máximo.

Nos podemos plantear el problema de la siguiente manera. Sujetamos el deslizador con la mano en un punto de la barra. Para cada posición del deslizador hay un valor del ángulo $θ$ . Si ahora quitamos la mano, ¿se mueve el deslizador o no?.

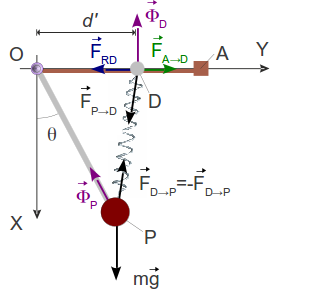
Llamamos $d'$ a la distancia desde el origen hasta el deslizador. El vector de posición del deslizador será

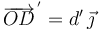
$\overrightarrow{OD}^{\,'} = d'\,\vec{\jmath}$

Una vez que hemos quitado la mano las fuerzas sobre el deslizador son

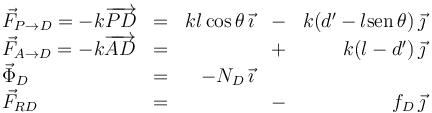
$\begin{array}{lcrcr} \vec{F}_{P\to D} = -k\overrightarrow{PD}& = & kl\cos\theta\,\vec{\imath} & - & k(d'-l\mathrm{sen}\,\theta)\,\vec{\jmath}\\ \vec{F}_{A\to D} = -k\overrightarrow{AD}& = & & + & k(l-d')\,\vec{\jmath} \\ \vec{\Phi}_D & = & -N_D\,\vec{\imath} & & \\ \vec{F}_{RD} & = & & - & f_D\,\vec{\jmath} \end{array}$

Escogemos el signo de la componente de la fuerza de rozamiento para que sea coherente con el dibujo.La suma de estas cuatro fuerzas ha de ser cero, de donde obtenemos

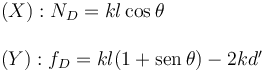
$\begin{array}{l} (X): N_D = kl\cos\theta \\ \\ (Y): f_D = kl(1+\mathrm{sen}\,\theta) - 2kd' \end{array}$

Por otro lado las fuerzas sobre la partícula $P$ son

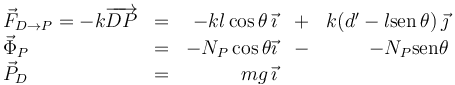
$\begin{array}{lcrcr} \vec{F}_{D\to P} = -k\overrightarrow{DP}& = &- kl\cos\theta\,\vec{\imath} & + & k(d'-l\mathrm{sen}\,\theta)\,\vec{\jmath}\\ \vec{\Phi}_P & = & -N_P\cos\theta\vec{\imath} & - & -N_P\mathrm{sen}\theta \\ \vec{P}_{D} & = & mg\,\vec{\imath} & & \end{array}$

La suma de estas dos fuerzas ha de ser cero, por tanto

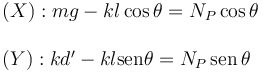
$\begin{array}{l} (X): mg - kl\cos\theta = N_P\cos\theta \\ \\ (Y): kd' - kl\mathrm{sen}\theta = N_P\,\mathrm{sen}\,\theta \end{array}$

Podemos eliminar $N P$ de estas dos ecuaciones

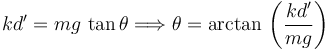
$kd' = mg\,\tan\theta \Longrightarrow \theta = \mathrm{arctan}\,\left(\dfrac{kd'}{mg}\right)$

Esta expresión nos da el valor del ángulo $θ$ en función de $d'$ . Para saber si la posición es de equilibrio hemos de comparar el módulo de la fuerza de rozamiento con su máximo valor posible

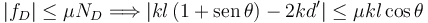
$|f_D| \leq \mu N_D \Longrightarrow |kl\,(1+\mathrm{sen}\,\theta)- 2kd'| \leq \mu kl\cos\theta$

El análisis detallado completo es complejo porque $f D$ puede ser positivo o negativo, según como sea la relación entre el peso y la fuerza de los muelles.

2.4 Energías cinética y potencial del punto P

La energía cinética del punto $P$ es

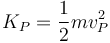
$K_P = \dfrac{1}{2}mv_P^2$

Para hallar la velocidad derivamos el vector de posición

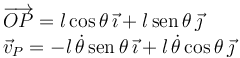
$\begin{array}{l} \overrightarrow{OP} = l\cos\theta\,\vec{\imath} + l\,\mathrm{sen}\,\theta\,\vec{\jmath}\\ \vec{v}_P = -l\,\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} + l\,\dot{\theta}\cos\theta\,\vec{\jmath} \end{array}$

El cuadrado del módulo es

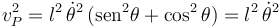
$v_P^2 = l^2\,\dot{\theta}^2\,(\mathrm{sen}^2\theta + \cos^2\theta) = l^2\,\dot{\theta}^2$

La energía cinética es

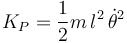
$K_P = \dfrac{1}{2}m\,l^2\,\dot{\theta}^2$

La partícula $P$ tiene dos energías potenciales, la gravitatoria y la elástica asociada el muelle que la une con el deslizador. Tomando como origen de energía potencial gravitatoria la altura $x = 0$ tenemos

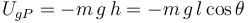
$U_{gP} = -m\,g\,h = -m\,g\,l\cos\theta$

Para la energía elástica tenemos

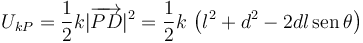
$U_{kP} = \dfrac{1}{2}k|\overrightarrow{PD}|^2= \dfrac{1}{2}k\,\left(l^2+d^2-2dl\,\mathrm{sen}\,\theta\right)$

siendo $d$ la distancia desde el origen al deslizador. Si no hay rozamiento, como en el primer apartado, podemos sustituir

$d=\dfrac{1}{2}l\,(1+\mathrm{sen}\,\theta)$

Barra conectada a un deslizador, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre $P$

2.2 Equilibrio para $\theta=60^{\circ}$

2.3 Análisis con rozamiento

2.4 Energías cinética y potencial del punto P

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra conectada a un deslizador, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas sobre P

2.2 Equilibrio para

2.3 Análisis con rozamiento

2.4 Energías cinética y potencial del punto P

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1 Fuerzas sobre $P$

2.2 Equilibrio para $\theta=60^{\circ}$