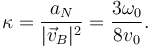De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una barra de longitud $L$ se mueve de modo que su extremo $A$ se desplaza sobre el eje $O Y$ con velocidad uniforme $v 0$ y el ángulo que forma la barra con el eje $O X$ es $θ = ω 0 t$ . En el instante inicial el punto $A$ estaba en el origen y la barra estaba horizontal, es decir $θ(0) = 0$ .

Escribe la expresión que da el vector de posición del punto $B$ .
Encuentra la aceleración del punto $B$ .
Si se cumple 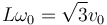$L\omega_0=\sqrt{3}v_0$ , ¿cuánto vale la aceleración tangencial del punto $B$ en el instante $t = π / 2ω 0$ ?
En ese mismo instante, y con el mismo valor de $L ω 0$ , cuánto vale la curvatura de la trayectoria del punto $B$ ?

2 Solución

2.1 Vector de posición del punto $B$

El vector de posición del punto $B$ puede escribirse como

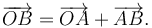
$\overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB}.$

El punto $A$ se mueve sobre el eje $O Y$ con velocidad uniforme. Si en el instante inicial estaba en el origen tenemos

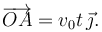
$\overrightarrow{OA} = v_0t\,\vec{\jmath}.$

El otro vector es

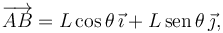
$\overrightarrow{AB} = L\cos\theta\,\vec{\imath} + L\,\mathrm{sen}\,\theta\,\vec{\jmath},$

donde, según el enunciado, tenemos $θ = ω 0 t$ . Por tanto, el vector pedido es

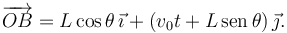
$\overrightarrow{OB} = L\cos\theta\,\vec{\imath} + (v_0t + L\,\mathrm{sen}\,\theta)\,\vec{\jmath}.$

2.2 Aceleración del punto $B$

La velocidad del punto $B$ es

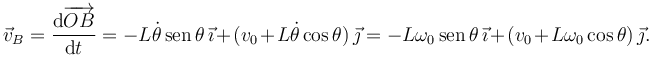
$\vec{v}_B = \dfrac{\mathrm{d}\overrightarrow{OB}}{\mathrm{d}t} = -L\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath} + (v_0 + L\dot{\theta}\cos\theta)\,\vec{\jmath} = -L\omega_0\,\mathrm{sen}\,\theta\,\vec{\imath} + (v_0 + L\omega_0\cos\theta)\,\vec{\jmath}.$

Hemos usado 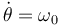$\dot{\theta}=\omega_0$ . Derivamos otra vez respecto al tiempo para obtener la aceleración

$\vec{a}_B = \dfrac{\mathrm{d}\vec{v}_B}{\mathrm{d}t} = -L\omega_0\dot{\theta}\cos\theta\,\vec{\imath} - L\omega_0\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\jmath} = -L\omega_0^2\cos\theta\,\vec{\imath} - L\omega_0^2\,\mathrm{sen}\,\theta\,\vec{\jmath}$

2.3 Aceleración tangencial y curvatura

En el instante indicado, $t = π / 2ω 0$ , tenemos

$θ(π / 2ω 0) = π / 2.$

La velocidad y la aceleración en ese instante son

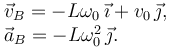
$\begin{array}{l} \vec{v}_B = -L\omega_0\,\vec{\imath} + v_0\,\vec{\jmath},\\ \vec{a}_B = -L\omega_0^2\,\vec{\jmath}. \end{array}$

El enunciado dice que consideremos la situación en que se cumple 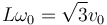$L\omega_0=\sqrt{3}v_0$ . Entonces

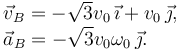
$\begin{array}{l} \vec{v}_B = -\sqrt{3}v_0\,\vec{\imath} + v_0\,\vec{\jmath},\\ \vec{a}_B = -\sqrt{3}v_0\omega_0\,\vec{\jmath}. \end{array}$

El módulo de la velocidad es

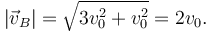
$|\vec{v}_B| = \sqrt{3v_0^2 + v_0^2} = 2v_0.$

La aceleración tangencial es

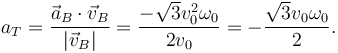
$a_T = \dfrac{\vec{a}_B\cdot\vec{v}_B}{|\vec{v}_B|} = \dfrac{-\sqrt{3}v_0^2\omega_0}{2v_0} = -\dfrac{\sqrt{3}v_0\omega_0}{2}.$

La aceleración normal en ese instante es

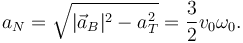
$a_N = \sqrt{|\vec{a}_B|^2-a_T^2} = \dfrac{3}{2}v_0\omega_0.$

Por lo que la curvatura es

$\kappa = \dfrac{a_N}{|\vec{v}_B|^2} = \dfrac{3\omega_0}{8v_0}.$

Barra con traslación y rotación (Nov. 2018 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector de posición del punto $B$

2.2 Aceleración del punto $B$

2.3 Aceleración tangencial y curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra con traslación y rotación (Nov. 2018 G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector de posición del punto B

2.2 Aceleración del punto B

2.3 Aceleración tangencial y curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.1 Vector de posición del punto $B$

2.2 Aceleración del punto $B$