Barra articulada rotando en un plano (MR G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Barra articulada rotando en un plano
3 Solución

1 Enunciado

2 Barra articulada rotando en un plano

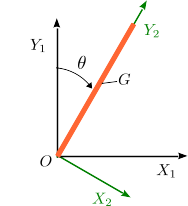
Se tiene una barra homogénea de longitud $L$ y masa $M$ . La barra tiene un extremo fijo en el punto $O$ y gira únicamente en el plano $O X 1 Y 1$ . La posición de la barra viene determinada por el ángulo $θ$ que forma con el eje $O Y 1$ .

Encuentra la expresión del momento cinético $\vec{L}_O$ de la barra y de su energía cinética $T$ .
Aplica el T.M.C. en $O$ para obtener una ecuación diferencial del movimiento.
Obtén una integral primera del movimiento. ¿Es equivalente a la ecuación anterior?

3 Solución

3.1 Momento cinético y energía cinética

La barra rota alrededor del punto fijo $O$ . Entonces el momento angular y la energía cinética se pueden calcular usando las expresiones

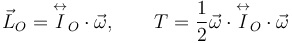
$\vec{L}_O = \overset\leftrightarrow{I}_O\cdot\vec{\omega}, \qquad T = \dfrac{1}{2}\vec{\omega}\cdot\overset\leftrightarrow{I}_O\cdot\vec{\omega}$

El eje de rotación es paralelo al eje 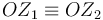$OZ_1\equiv OZ_2$ . Con el sentido del ángulo indicado en la figura el vector rotación es

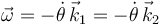
$\vec{\omega} = -\dot{\theta}\,\vec{k}_1 = -\dot{\theta}\,\vec{k}_2$

Expresamos el tensor de inercia de la barra en el punto $O$ en la base del sólido solidario con la barra

$\overset\leftrightarrow{I}_O = I \left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1 \end{array} \right]_2$

con

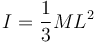
$I = \dfrac{1}{3}ML^2$

El momento angular es

$\vec{L}_O = \overset\leftrightarrow{I}_O\cdot\vec{\omega} = I \left[ \begin{array}{ccc} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1 \end{array} \right]_2 \left[ \begin{array}{c} 0\\ 0\\ -\dot{\theta} \end{array} \right]_2 = -I\dot{\theta} \left[ \begin{array}{c} 0\\ 0\\ 1 \end{array} \right]_2 = -I\dot{\theta}\,\vec{k}_{1,2}$

La energía cinética es

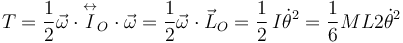
$T = \dfrac{1}{2}\vec{\omega}\cdot\overset\leftrightarrow{I}_O\cdot\vec{\omega} = \dfrac{1}{2}\vec{\omega}\cdot\vec{L}_O = \dfrac{1}{2}\,I\dot{\theta}^2= \dfrac{1}{6}ML2\dot{\theta}^2$

3.2 Aplicación del T.M.C.

La barra está sometida a dos fuerzas, el peso aplicado en el punto $G$ y la fuerza de reacción vincular en $O$ . Aplicando el T.M.C. en el punto $O$ tenemos

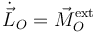
$\dot{\vec{L}}_O = \vec{M}^{\mathrm{ext}}_O$

La fuerza aplicada en $O$ no ejerce momento respecto a $O$ . El momento neto es

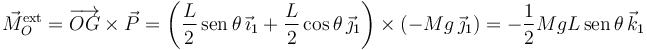
$\vec{M}^{\mathrm{ext}}_O = \overrightarrow{OG}\times\vec{P} = \left(\dfrac{L}{2}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + \dfrac{L}{2}\cos\theta\,\vec{\jmath}_1\right)\times(-Mg\,\vec{\jmath}_1) = -\dfrac{1}{2}MgL\,\mathrm{sen}\,\theta\,\vec{k}_1$

Por otro lado, la derivada respecto del tiempo del momento cinético es

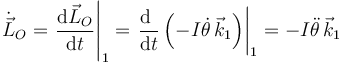
$\dot{\vec{L}}_O = \left.\dfrac{\mathrm{d}\vec{L}_O}{\mathrm{d}t}\right|_1= \left.\dfrac{\mathrm{d}\ }{\mathrm{d}t}\left(-I\dot{\theta}\,\vec{k}_1\right)\right|_1= -I\ddot{\theta}\,\vec{k}_1$

Visto desde el sólido "1", el vector $\vec{k}_2=\vec{k}_1$ no cambia, y la constante $I$ tampoco. La ecuación de movimiento es

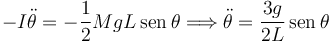
$-I\ddot{\theta} = -\dfrac{1}{2}MgL\,\mathrm{sen}\,\theta \Longrightarrow \ddot{\theta} = \dfrac{3g}{2L}\,\mathrm{sen}\,\theta$

3.3 Integral primera del movimiento

La fuerza de reacción vincular en $O$ no hace trabajo, pues el punto $O$ no se mueve. El peso es una fuerza conservativa, y podemos asociarle una energía potencial gravitatoria. Tomando como referencia de energía potencial $y 1 = 0$ , la energía potencial gravitatoria de la barra es

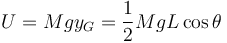
$U = Mgy_G = \dfrac{1}{2}MgL\cos\theta$

La energía mecánica es la suma de la cinética y la potencial gravitatoria

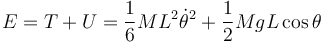
$E = T + U = \dfrac{1}{6}ML^2\dot{\theta}^2 + \dfrac{1}{2}MgL\cos\theta$

Al ser constante, la energía mecánica en cada instante es igual a la que tenía en el instante inicial. Si las condiciones iniciales son $θ(0) = θ 0$ y 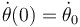$\dot{\theta}(0)=\dot{\theta}_0$ la energía mecánica en el instante inicial es

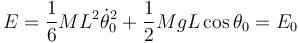
$E = \dfrac{1}{6}ML^2\dot{\theta}_0^2 + \dfrac{1}{2}MgL\cos\theta_0 = E_0$

Con esto obtenemos la ecuación diferencial del movimiento

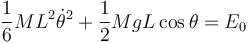
$\dfrac{1}{6}ML^2\dot{\theta}^2 + \dfrac{1}{2}MgL\cos\theta = E_0$

donde $E 0$ es constante en el tiempo.

A diferencia de la ecuación obtenida en el apartado anterior, esta es una ecuación diferencial de primer orden. Sin embargo, ambas ecuaciones son equivalentes. Si derivamos respecto al tiempo tenemos

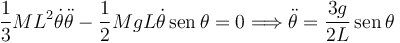
$\dfrac{1}{3}ML^2\dot{\theta}\ddot{\theta} - \dfrac{1}{2}MgL\dot{\theta}\,\mathrm{sen}\,\theta = 0 \Longrightarrow \ddot{\theta} = \dfrac{3g}{2L}\,\mathrm{sen}\,\theta$

Reobtenemos la ecuación diferencial de segundo orden. Por esto la ecuación obtenida de la conservación de la energía se llama integral primera. Es equivalente a integrar una vez la ecuación diferencial de segundo orden obtenida de aplicar el T.M.C.

Barra articulada rotando en un plano (MR G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Barra articulada rotando en un plano

3 Solución

3.1 Momento cinético y energía cinética

3.2 Aplicación del T.M.C.

3.3 Integral primera del movimiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES