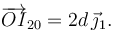De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

La barra de la figura (sólido "2") está articulada en el punto $O$ . Se apoya sobre el vértice $A$ de una placa rectangular (sólido "0") de altura $d$ . El vértice $A$ de la placa puede deslizar a lo largo de la barra. La placa desliza sobre el eje $O X 1$ , de forma que su base está siempre en contacto con el eje. El ángulo que forma la barra con el eje $O X 1$ es $θ(t) = ω 0 t + π / 6$ , con $ω 0$ constante y positivo.

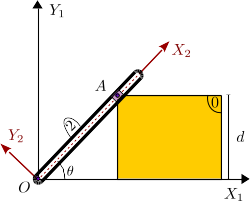
Escribe el vector de posición absoluto del punto $A$ del sólido "0".
Encuentra la reducción cinemática de los tres movimientos relativos del sistema.
Determina aceleración 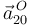$\vec{a}^{\,O}_{20}$ en el instante en que $θ = π / 4$ , así como la posición del C.I.R.
Determina las posiciones de los C.I.R en ese mismo instante.

2 Solución

2.1 Vector de posición

El vector de posición pedido es

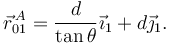
$\vec{r}^{\,A}_{01} = \dfrac{d}{\tan\theta}\vec{\imath}_1 + d\vec{\jmath}_1.$

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

Este movimiento es una traslación, pues los lados de la placa mantienen sus direcciones constantes respecto a los ejes del sólido "1". El vector de posición del apartado anterior sigue siempre al mismo punto $A$ del sólido "0". Entonces se puede derivar respecto del tiempo para calcular la velocidad 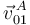$\vec{v}^{\,A}_{01}$ . Al ser una traslación, no hay que poner la letra, pues todos los puntos del sólido tienen la misma velocidad.

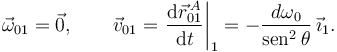
$\vec{\omega}_{01} = \vec{0}, \qquad \vec{v}_{01} = \left. \dfrac{\mathrm{d}\vec{r}^{\,A}_{01}}{\mathrm{d}t} \right|_1 = -\dfrac{d\omega_0}{\mathrm{sen}^2\,\theta}\,\vec{\imath}_1.$

2.2.2 Movimiento {21}

Esta es una rotación de eje permanente con C.I.R. en el punto $O$ . Tenemos

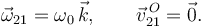
$\vec{\omega}_{21} = \omega_0\,\vec{k}, \qquad \vec{v}^{\,O}_{21} = \vec{0}.$

2.2.3 Movimiento {20}

Usamos las leyes de composición. Tenemos

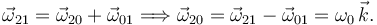
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = \omega_0\,\vec{k}.$

Y

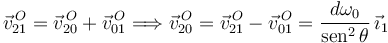
$\vec{v}^{\,O}_{21} = \vec{v}^{\,O}_{20} + \vec{v}^{\,O}_{01} \Longrightarrow \vec{v}^{\,O}_{20} = \vec{v}^{\,O}_{21} - \vec{v}^{\,O}_{01} = \dfrac{d\omega_0}{\mathrm{sen}^2\,\theta}\,\vec{\imath}_1$

2.3 Derivadas de las reducciones cinemáticas

2.3.1 Movimiento {01}

Derivando respecto al tiempo tenemos

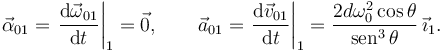
$\vec{\alpha}_{01} = \left. \dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t} \right|_1 = \vec{0}, \qquad \vec{a}_{01} = \left. \dfrac{\mathrm{d}\vec{v}_{01}}{\mathrm{d}t} \right|_1 = \dfrac{2d\omega^2_0\cos\theta}{\mathrm{sen}^3\,\theta}\,\vec{\imath}_1.$

2.3.2 Movimiento {21}

Derivando tenemos

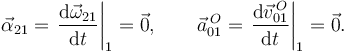
$\vec{\alpha}_{21} = \left. \dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t} \right|_1 = \vec{0}, \qquad \vec{a}^{\,O}_{01} = \left. \dfrac{\mathrm{d}\vec{v}^{\,O}_{01}}{\mathrm{d}t} \right|_1 = \vec{0}.$

2.3.3 Movimiento {20}

Usamos las leyes de composición. Tenemos

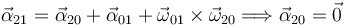
$\vec{\alpha}_{21} = \vec{\alpha}_{20} + \vec{\alpha}_{01} +\vec{\omega}_{01}\times\vec{\omega}_{20} \Longrightarrow \vec{\alpha}_{20} = \vec{0}$

Y

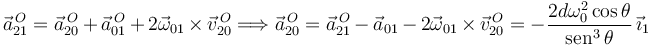
$\vec{a}^{\,O}_{21} = \vec{a}^{\,O}_{20} + \vec{a}^{\,O}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,O}_{20} \Longrightarrow \vec{a}^{\,O}_{20} = \vec{a}^{\,O}_{21} - \vec{a}_{01} - 2\vec{\omega}_{01}\times\vec{v}^{\,O}_{20} = -\dfrac{2d\omega^2_0\cos\theta}{\mathrm{sen}^3\,\theta}\,\vec{\imath}_1$

Si $θ = π / 4$ tenemos

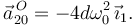
$\vec{a}^{\,O}_{20} = -4d\omega_0^2\,\vec{\imath}_1.$

2.4 Posición de los C.I.R en $θ = π / 4$

La figura de la derecha muestra la posición de los C.I.R. de los movimientos cuando $θ = π / 4$ . En todo instante tenemos

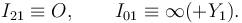
$I_{21}\equiv O, \qquad I_{01}\equiv \infty (+Y_1).$

Por el Teorema de los centros, el $I 20$ debe estar en la línea que une $I 21$ y $I 01$ , esto es, el eje $O Y 1$ . Por otro lado, la velocidad 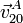$\vec{v}^{A}_{20}$ debe ser paralela a la propia barra, pues ésta no puede penetrar en la placa. Por tanto, el $I 20$ debe estar en la línea perpendicular a la barra trazada por $A$ . El punto de corte de estas dos líneas da la posición del $I 20$ . Cuando $θ = π / 4$ tenemos

$\overrightarrow{OI}_{20} = 2d\,\vec{\jmath}_1.$

Barra apoyada sobre placa rectangular (Nov 2017 MR)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector de posición

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

2.2.2 Movimiento {21}

2.2.3 Movimiento {20}

2.3 Derivadas de las reducciones cinemáticas

2.3.1 Movimiento {01}

2.3.2 Movimiento {21}

2.3.3 Movimiento {20}

2.4 Posición de los C.I.R en $θ = π / 4$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Barra apoyada sobre placa rectangular (Nov 2017 MR)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vector de posición

2.2 Reducciones cinemáticas

2.2.1 Movimiento {01}

2.2.2 Movimiento {21}

2.2.3 Movimiento {20}

2.3 Derivadas de las reducciones cinemáticas

2.3.1 Movimiento {01}

2.3.2 Movimiento {21}

2.3.3 Movimiento {20}

2.4 Posición de los C.I.R en θ = π / 4

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.4 Posición de los C.I.R en $θ = π / 4$