Barra apoyada con resorte (GIOI)

De Laplace

1 Enunciado

Se tiene un sistema formado por una varilla de masa $m = 1.2 k g$ y longitud 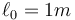$\ell_0=1 m$ , apoyada sin rozamiento en una pared vertical y un suelo horizontal. El extremo B, apoyado en la pared, está conectado a la esquina mediante un resorte de constante $k = 30 N / m$ y longitud natural 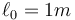$\ell_0=1 m$ . Por efecto de la gravedad (tómese $g = 10 m / s 2$ ) la varilla tiende a bajar, pero el resorte la empuja hacia arriba, existiendo una posición de equilibrio.

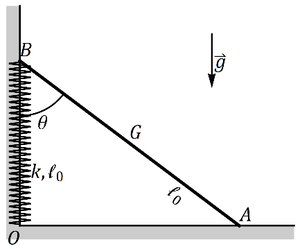
Determine la posición de los extremos A y B de la barra en la posición de equilibrio.
Halle las fuerzas de reacción en la pared y en el suelo en esta posición de equilibrio.
Suponga ahora que la barra se sitúa inicialmente en la posición vertical en reposo. Se le comunica un ligerísimo impulso, de manera que comienza a resbalar.
1. Calcule la posición de A y B en el momento en que el muelle se comprime al máximo (a partir del cual la barra vuelve a subir).
2. Durante el descenso, la barra pasa (en movimiento) por la posición de equilibrio. Calcule la velocidad de A, de B y del centro de masas, G, en ese instante.

2 Posición de equilibrio

La condición de equilibrio de un sólido la da el que la resultante de las fuerzas se anule y también lo haga el momento resultante respecto a cualquier punto.

$\vec{F}=\vec{0}\qquad\qquad \vec{M}_O=\vec{0}$

Las fuerzas que actúan sobre el sólido son

El peso

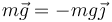
$m\vec{g}=-mg\vec{\jmath}$

La fuerza elástica debida al resorte

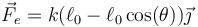
$\vec{F}_e=k(\ell_0-\ell_0\cos(\theta))\vec{\jmath}$

siendo θ el ángulo que la barra forma con la vertical

La fuerza de reacción con el suelo

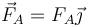
$\vec{F}_A=F_A\vec{\jmath}$

La fuerza de reacción con el suelo

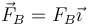
$\vec{F}_B=F_B\vec{\imath}$

La condición de resultante nula nos da las ecuaciones, separando por componentes

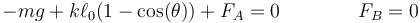
$-mg+k\ell_0(1-\cos(\theta))+F_A=0\qquad\qquad F_B=0$

Para completar el sistema necesitamos que también se anulen los momentos. Nos vale cualquier punto. Si lo hacemos respecto a la esquina, O,

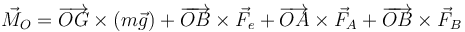
$\vec{M}_O=\overrightarrow{OG}\times(m\vec{g})+\overrightarrow{OB}\times\vec{F}_e+\overrightarrow{OA}\times\vec{F}_A+\overrightarrow{OB}\times\vec{F}_B$

Esto nos da la ecuación

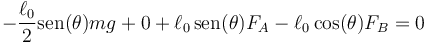
$-\frac{\ell_0}{2}\mathrm{sen}(\theta)mg+0+\ell_0\,\mathrm{sen}(\theta)F_A-\ell_0\cos(\theta)F_B=0$

de la cual obtenemos

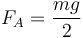
$F_A=\frac{mg}{2}$

y, por tanto,

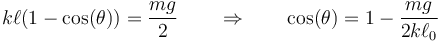
$k\ell(1-\cos(\theta))=\frac{mg}{2}\qquad\Rightarrow \qquad \cos(\theta)=1-\frac{mg}{2k\ell_0}$

siendo el valor numérico

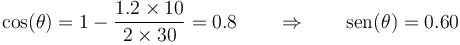
$\cos(\theta)=1-\frac{1.2\times 10}{2\times30}=0.8\qquad\Rightarrow\qquad \mathrm{sen}(\theta)=0.60$

Por ello, las posiciones de los puntos A y B se encuentran en

$\overrightarrow{OA}=\ell_0\mathrm{sen}(\theta)\vec{\imath}=0.60\vec{\imath}\,\mathrm{m}\qquad\qquad \overrightarrow{OB}=\ell_0\cos(\theta)\vec{\jmath}=0.80\vec{\jmath}\,\mathrm{m}$

Barra apoyada con resorte (GIOI)

De Laplace

1 Enunciado

2 Posición de equilibrio

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES