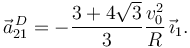De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

El disco de la figura (sólido "0"), de radio $R$ , rueda sin deslizar sobre el eje $O 1 X 1$ . El centro del disco se mueve con rapidez constante $v 0$ , como se indica en la figura. Una barra (sólido "2") de longitud $2 R$ está articulada en el punto $B$ de la circunferencia exterior del disco. El otro extremo de la barra desliza sobre el eje $O 1 X 1$ .

Localiza gráficamente los C.I.R. de los movimientos {01}, {20} y {21} en el instante indicado en la figura. Explica el procedimiento seguido.
Encuentra reducciones cinemáticas de los tres movimientos relativos indicados.
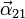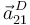Calcula $\vec{\alpha}_{21}$ y $\vec{a}^{\,D}_{21}$ .

2 Solución

2.1 Análisis previo

Del planteamiento del problema podemos deducir los siguientes puntos:

Todos los movimientos son planos, por tanto todos los vectores rotación y aceleración angular son perpendiculares al plano del movimiento.
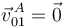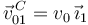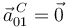EL disco rueda sin deslizar, entonces $\vec{v}^{\,A}_{01}=\vec{0}$ . Además del enunciado sabemos que $\vec{v}^{\,C}_{01}=v_0\,\vec{\imath}_1$ . Se dice que esta velocidad es constante, por tanto, $\vec{a}^{\,C}_{01} = \vec{0}$ .
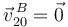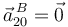Los sólidos "0" y "2" están articulados en $B$ en todo instante, por tanto $\vec{v}^{\,B}_{20}=\vec{0}$ y $\vec{a}^{\,B}_{20}=\vec{0}$ .
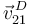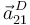El punto $D$ de la barra desliza desliza siempre sobre el eje $O 1 X 1$ , es decir, $\vec{v}^{\,D}_{21}$ y $\vec{a}^{\,D}_{21}$ son siempre paralelas a ese eje.
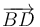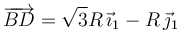Vamos a necesitar el vector $\overrightarrow{BD}$ . En la figura del siguiente apartado vemos que el triángulo $B E D$ es rectángulo. Usando el Teorema de Pitágoras tenemos $\overrightarrow{BD} = \sqrt{3}R\,\vec{\imath}_1 - R\,\vec{\jmath}_1$ .

2.2 Localización de los C.I.R.

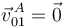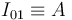Del análisis previo tenemos $\vec{v}^{\,A}_{01}=\vec{0}$ , por lo que $I_{01}\equiv A$ .

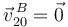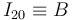También sabemos que $\vec{v}^{\,B}_{20}=\vec{0}$ . Entonces $I_{20}\equiv B$ .

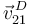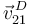Como $\vec{v}^{\,D}_{21}$ es siempre paralela al eje $O 1 X 1$ , el CIR $I 21$ debe estar en la línea perpendicular a $\vec{v}^{\,D}_{21}$ trazada por $D$ . Por otro lado, usando el Teorema de los Tres Centros, $I 21$ debe estar en la línea que une $I 01$ y $I 20$ . El CIR buscado está en el corte de esas dos líneas.

Aunque no se pedía en el examen, podemos obtener la localización exacta de $I 21$ . Como se ve en la figura, la línea que une $I 01$ y $I 20$ forma un ángulo $π / 4$ con la horizontal. Usando el Teorema de Pitágoras, tenemos

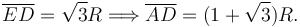
$\overline{ED} = \sqrt{3}R \Longrightarrow \overline{AD} = (1+\sqrt{3})R.$

Entonces

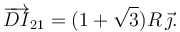
$\overrightarrow{DI}_{21} = (1+\sqrt{3})R\,\vec{\jmath}.$

2.3 Reducciones cinemáticas

2.3.1 Movimiento {01}

A partir del análisis anterior podemos escribir

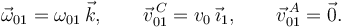
$\vec{\omega}_{01} = \omega_{01}\,\vec{k}, \qquad \vec{v}^{\,C}_{01} = v_0\,\vec{\imath}_1,\qquad \vec{v}^{\,A}_{01} = \vec{0}.$

Usando el Teorema de Chasles

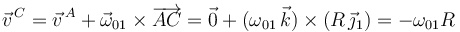
$\vec{v}^{\,C} = \vec{v}^{\,A} + \vec{\omega}_{01}\times\overrightarrow{AC} = \vec{0} + (\omega_{01}\,\vec{k})\times(R\,\vec{\jmath}_1) = -\omega_{01}R$

Comparando con el valor dado de 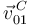$\vec{v}^{\,C}_{01}$ obtenemos

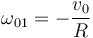
$\omega_{01} = -\dfrac{v_0}{R}$

Por tanto la reducción cinemática es

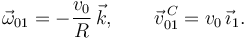
$\vec{\omega}_{01} = -\dfrac{v_0}{R}\,\vec{k},\qquad \vec{v}^{\,C}_{01} = v_0\,\vec{\imath}_1.$

También se puede hacer la reducción en el punto $A$ .

2.3.2 Movimiento {21}

La clave para resolver este apartado es que es un movimiento plano del que conocemos la velocidad del movimiento {21} en un punto (el $B$ ) y la dirección de la velocidad en otro (el $D$ ). Sabemos que

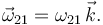
$\vec{\omega}_{21} = \omega_{21}\,\vec{k}.$

Usando la composición

${21} = {20} + {01}$

obtenemos

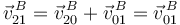
$\vec{v}^{\,B}_{21} = \vec{v}^{\,B}_{20} + \vec{v}^{\,B}_{01} = \vec{v}^{\,B}_{01}$

A partir de la ecuación del campo de velocidades del movimiento {01} obtenemos

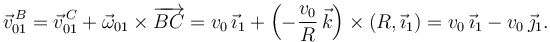
$\vec{v}^{\,B}_{01} = \vec{v}^{\,C}_{01} + \vec{\omega}_{01}\times\overrightarrow{BC} = v_0\,\vec{\imath}_1 + \left(-\dfrac{v_0}{R}\,\vec{k}\right)\times(R,\vec{\imath}_1) = v_0\,\vec{\imath}_1 - v_0\,\vec{\jmath}_1.$

Es decir

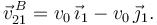
$\vec{v}^{\,B}_{21} = v_0\,\vec{\imath}_1 - v_0\,\vec{\jmath}_1.$

Por otro lado sabemos la dirección de 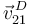$\vec{v}^{\,D}_{21}$ , paralela a $O 1 X 1$ . Con el Teorema de Chasles calculamos la velocidad {21} en $D$ a partir de $B$

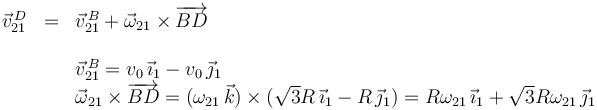
$\begin{array}{lcl} \vec{v}^{\,D}_{21} &=& \vec{v}^{\,B}_{21} + \vec{\omega}_{21}\times\overrightarrow{BD}\\ &&\\ &&\vec{v}^{\,B}_{21} = v_0\,\vec{\imath}_1 - v_0\,\vec{\jmath}_1\\ &&\vec{\omega}_{21}\times\overrightarrow{BD} = (\omega_{21}\,\vec{k})\times(\sqrt{3}R\,\vec{\imath}_1 -R\,\vec{\jmath}_1) = R\omega_{21}\,\vec{\imath}_1 + \sqrt{3}R\omega_{21}\,\vec{\jmath}_1 \end{array}$

El vector 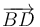$\overrightarrow{BD}$ lo hemos obtenido usando el Teorema de Pitágoras, como se ve en la figura del apartado anterior. Entonces

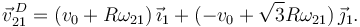
$\vec{v}^{\,D}_{21} = (v_0 + R\omega_{21})\,\vec{\imath}_1 + (-v_0 + \sqrt{3}R\omega_{21})\,\vec{\jmath}_1.$

La componente en $\vec{\jmath}_1$ tiene que ser cero, por tanto

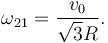
$\omega_{21} = \dfrac{v_0}{\sqrt{3}R}.$

Por tanto, una posible reducción cinemática de este movimiento es

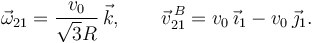
$\vec{\omega}_{21} = \dfrac{v_0}{\sqrt{3}R}\,\vec{k}, \qquad \vec{v}^{\,B}_{21} = v_0\,\vec{\imath}_1 - v_0\,\vec{\jmath}_1.$

2.3.3 Movimiento {20}

Usando la composición ${21} = {20} + {01}$ tenemos

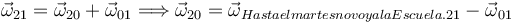
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{20} = \vec{\omega}_{ Hasta el martes no voy a la Escuela. 21} - \vec{\omega}_{01}$

Una posible reducción cinemática de este movimiento es

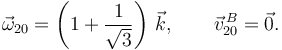
$\vec{\omega}_{20} = \left(1+\dfrac{1}{\sqrt{3}}\right)\,\vec{k}, \qquad \vec{v}^{\,B}_{20} = \vec{0}.$

2.4 Aceleraciones

Igual que para la reducción cinemática del movimiento {21}, la clave para resolver este apartado es que es un movimiento plano del que podemos conocer la aceleración del movimiento {21} en un punto (el $B$ ) y la dirección de la aceleración en otro (el $D$ ).

Del análisis previo sabemos

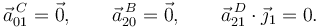
$\vec{a}^{\,C}_{01} = \vec{0}, \qquad \vec{a}^{\,B}_{20} = \vec{0}, \qquad \vec{a}^{\,D}_{21}\cdot\vec{\jmath}_1=0.$

Además, al ser $v 0$ constante, $\vec{\omega}_{01}$ también lo es, por lo que

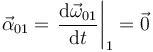
$\vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1 = \vec{0}$

Usando el Teorema de Coriolis

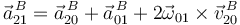
$\vec{a}^{\,B}_{21} = \vec{a}^{\,B}_{20} + \vec{a}^{\,B}_{01} + 2\vec{\omega}_{01}\times\vec{v}^{\,B}_{20}$

Sólo el segundo término es no nulo. Como es un movimiento tenemos

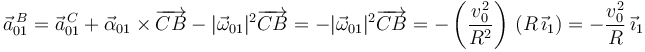
$\vec{a}^{\,B}_{01} = \vec{a}^{\,C}_{01} + \vec{\alpha}_{01}\times\overrightarrow{CB} - |\vec{\omega}_{01}|^2\overrightarrow{CB} = - |\vec{\omega}_{01}|^2\overrightarrow{CB} = -\left(\dfrac{v_0^2}{R^2}\right)\,(R\,\vec{\imath}_1) = -\dfrac{v_0^2}{R}\,\vec{\imath}_1$

Entonces

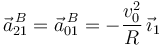
$\vec{a}^{\,B}_{21} = \vec{a}^{\,B}_{01} = -\dfrac{v_0^2}{R}\,\vec{\imath}_1$

Sabemos que 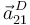$\vec{a}^{\,D}_{21}$ debe ser paralela al eje $O 1 X 1$ . Usando la ecuación del campo de aceleraciones del movimiento {21}, que es plano, tenemos

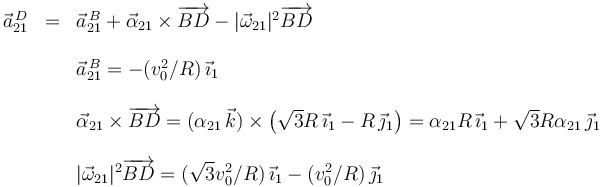
$\begin{array}{lcl} \vec{a}^{\,D}_{21} & = & \vec{a}^{\,B}_{21} + \vec{\alpha}_{21}\times\overrightarrow{BD} - |\vec{\omega}_{21}|^2\overrightarrow{BD}\\ &&\\ & & \vec{a}^{\,B}_{21} = -(v_0^2/R)\,\vec{\imath}_1\\ &&\\ &&\vec{\alpha}_{21}\times\overrightarrow{BD} = (\alpha_{21}\,\vec{k})\times\left(\sqrt{3}R\,\vec{\imath}_1 - R\,\vec{\jmath}_1\right) = \alpha_{21}R\,\vec{\imath}_1 +\sqrt{3}R\alpha_{21}\,\vec{\jmath}_1\\ &&\\ &&|\vec{\omega}_{21}|^2\overrightarrow{BD} = (\sqrt{3}v_0^2/R)\,\vec{\imath}_1 - (v_0^2/R)\,\vec{\jmath}_1 \end{array}$

Entonces

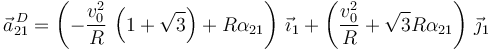
$\vec{a}^{\,D}_{21} = \left(-\dfrac{v_0^2}{R}\,\left(1+\sqrt{3}\right) + R\alpha_{21}\right)\,\vec{\imath}_1 + \left(\dfrac{v_0^2}{R}+\sqrt{3}R\alpha_{21}\right)\,\vec{\jmath}_1$

La componente en 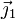$\vec{\jmath}_1$ debe se nula, por tanto

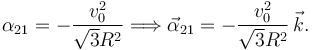
$\alpha_{21} = -\dfrac{v_0^2}{\sqrt{3}R^2} \Longrightarrow \vec{\alpha}_{21} = -\dfrac{v_0^2}{\sqrt{3}R^2}\,\vec{k}.$

Aplicando esto a la expresión de 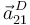$\vec{a}^{\,D}_{21}$ obtenemos

$\vec{a}^{\,D}_{21} = -\dfrac{3+4\sqrt{3}}{3}\dfrac{v_0^2}{R}\,\vec{\imath}_1.$

Aro con barra articulada, Enero 2018 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Análisis previo

2.2 Localización de los C.I.R.

2.3 Reducciones cinemáticas

2.3.1 Movimiento {01}

2.3.2 Movimiento {21}

2.3.3 Movimiento {20}

2.4 Aceleraciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES