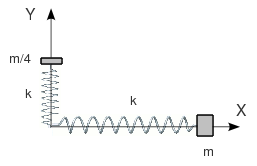
Entrar Página Discusión Historial Go to the site toolbox

Aplicación: Dos muelles oscilando en direcciones perpendiculares

De Laplace

Contenido

1 Enunciado

Sobre una mesa horizontal se encuentran dos resortes ideales sin masa, misma constante k y longitud natural nula. Los dos resortes están atados al centro de la mesa. Atados a los muelles se encuentran una masa m y una masa m / 4. En un momento dado, la primera masa se lleva al punto 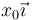x_0\vec{\imath} del centro soltándola desde el reposo, mientras que a la segunda masa, situada en el origen, se le comunica una velocidad v_0\vec{\jmath}.

  1. Determina la posición del CM a partir de ese instante. ¿Describe un movimiento periódico? ¿Con qué periodo?
  2. Halla la energía cinética y el momento cinético del sistema.


2 Solución

2.1 Movimiento de cada masa

El sistema consiste en dos masas puntuales acoplada cada una de ellas a un muelle sin masa de constante recuperadora k. Cada una de las masas realiza un movimiento armónico simple (MAS) en la dirección del muelle. Si llamamos m1 a la masa que se mueve a lo largo del eje X y m2 a la que lo hace a lo largo del eje Y el vector de posición de cada una de las masas se puede escribir

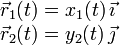
\begin{array}{l} \vec{r}_1(t) = x_1(t)\,\vec{\imath}\\ \vec{r}_2(t) = y_2(t)\,\vec{\jmath} \end{array}

Cada una de las componentes cumple la ecuación del oscilador armónico, con la frecuencia correspondiente a la combinación de su masa y la constante recuperadora del muelle

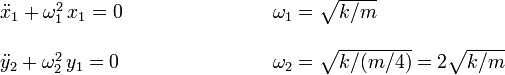
\begin{array}{lcl} \ddot{x}_1 + \omega_1^2\,x_1 = 0&\qquad\qquad\qquad& \omega_1 = \sqrt{k/m}\\ &&\\ \ddot{y}_2 + \omega_2^2\,y_1 = 0&\qquad\qquad\qquad& \omega_2 = \sqrt{k/(m/4)} = 2\sqrt{k/m} \end{array}

Vemos que ω2 = 2ω1. Para simplificar escribimos

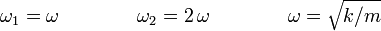
\omega_1 = \omega \qquad\qquad \omega_2 = 2\,\omega\qquad\qquad \omega=\sqrt{k/m}

La solución general de la ecuación del oscilador armónico puede escribirse de dos formas

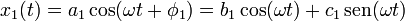
x_1(t) = a_1\cos(\omega t + \phi_1) = b_1\cos(\omega t) + c_1\,\mathrm{sen}(\omega t)

En el primer caso las constantes que hay que determinar a partir de las condiciones de contorno son a1 y φ1 y en el segundo b1 y c1. En este caso el cálculo es ligeramente más simple si escogemos la segunda forma.

2.1.1 Masa sobre el eje X

El enunciado nos dice que la masa que se mueve horizontalmente se suelta con velocidad nula desde una distancia x0 del origen. Por tanto, las condiciones iniciales son

x_1(0) = x_0\qquad\qquad \dot{x}_1(0)=0

La solución de la ecuación del MAS se escribe

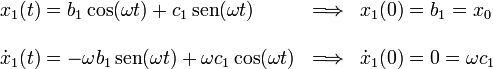
\begin{array}{lcl} x_1(t) = b_1\cos(\omega t) + c_1\,\mathrm{sen}(\omega t) & \Longrightarrow & x_1(0) = b_1=x_0\\ && \\ \dot{x}_1(t) = -\omega b_1\,\mathrm{sen}(\omega t) + \omega c_1\,\mathrm{cos}(\omega t) & \Longrightarrow & \dot{x}_1(0) = 0 = \omega c_1 \end{array}

Por tanto, el vector de posición de la masa 1 es

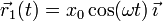
\vec{r}_1(t)=x_0\cos(\omega t) \,\vec{\imath}

2.1.2 Masa sobre el eje Y

El procedimiento es similar para la masa que se mueve verticalmente. Esta parte desde el origen con velocidad inicial 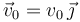\vec{v}_0 = v_0\,\vec{\jmath} . Por tanto las condiciones iniciales son

y_2(0) = 0\qquad\qquad \dot{y}_2(0)=v_0

La solución de la ecuación del MAS se escribe

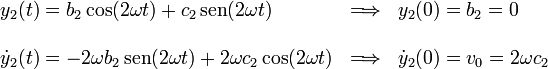
\begin{array}{lcl} y_2(t) = b_2\cos(2\omega t) + c_2\,\mathrm{sen}(2\omega t) & \Longrightarrow & y_2(0) = b_2=0\\ && \\ \dot{y}_2(t) = -2\omega b_2\,\mathrm{sen}(2\omega t) + 2\omega c_2\,\mathrm{cos}(2\omega t) & \Longrightarrow & \dot{y}_2(0) = v_0 = 2\omega c_2 \end{array}

Por tanto, el vector de posición de la masa 1 es

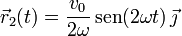
\vec{r}_2(t)=\frac{v_0}{2\omega}\,\mathrm{sen}(2\omega t) \,\vec{\jmath}

2.2 Posición del centro de masas

Ahora basta con aplicar la fórmula que nos da la posición del centro de masas de un sistema de partículas.

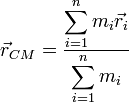
\vec{r}_{CM} = \frac{\displaystyle \sum\limits_{i=1}^n m_i\vec{r}_i}{\displaystyle \sum\limits_{i=1}^nm_i}

En este caso tenemos sólo dos masas, por tanto

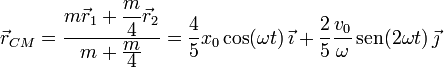
\vec{r}_{CM} = \frac{\displaystyle m\vec{r}_1 + \frac{m}{4}\vec{r}_2}{m+\frac{\displaystyle m}{\displaystyle 4}} = \frac{4}{5}x_0\cos(\omega t)\,\vec{\imath} + \frac{2}{5}\frac{v_0}{\omega}\,\mathrm{sen}(2\omega t)\,\vec{\jmath}

Cada uno de las componentes es periódica. El período de cada una de ellas es

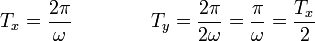
T_x = \frac{2\pi}{\omega} \qquad\qquad T_y = \frac{2\pi}{2\omega} = \frac{\pi}{\omega} = \frac{T_x}{2}

Cada intervalo de tiempo 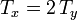T_x =2\,T_y las posiciones y velocidades de ambas masas son iguales a las iniciales. Por tanto el movimiento es periódico con período

T = 2π / ω

2.3 Energía cinética del sistema

La energía cinética de un sistema de partículas es

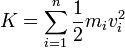
K = \sum\limits_{i=1}^n \frac{\displaystyle 1}{\displaystyle 2}m_iv_i^2

Para cada masa su velocidad es

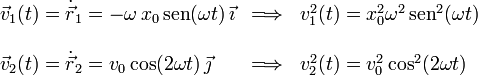
\begin{array}{lcl} \vec{v}_1(t) = \dot{\vec{r}}_1 = -\omega\,x_0\,\mathrm{sen}(\omega t)\,\vec{\imath} &\Longrightarrow& v_1^2(t) = x_0^2\omega^2\,\mathrm{sen}^2(\omega t) \\ && \\ \vec{v}_2(t) = \dot{\vec{r}}_2 = v_0\,\mathrm{cos}(2\omega t)\,\vec{\jmath} &\Longrightarrow& v_2^2(t) = v_0^2\,\mathrm{cos}^2(2\omega t) \end{array}

La energía cinética es

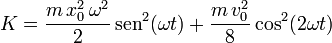
K = \frac{m\,x_0^2\,\omega^2}{2}\,\mathrm{sen}^2(\omega t) + \frac{m\,v_0^2}{8}\cos^2(2\omega t)

2.4 Momento cinético del sistema

El momento cinético de un sistema respecto del origen es

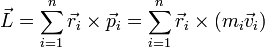
\vec{L} = \sum\limits_{i=1}^n \vec{r}_i\times\vec{p}_i = \sum\limits_{i=1}^n \vec{r}_i\times(m_i\vec{v}_i)

En este caso, no hace falta hacer ningún cálculo. Las velocidades de cada masa tienen la forma

\vec{v}_1(t) = v_1(t)\,\vec{\imath} \qquad\qquad \vec{v}_2(t) = v_2(t)\,\vec{\jmath}

Por tanto, el momento cinético total es

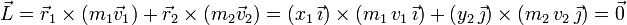
\vec{L} = \vec{r}_1\times(m_1\vec{v}_1) + \vec{r}_2\times(m_2\vec{v}_2)= (x_1\,\vec{\imath})\times(m_1\,v_1\,\vec{\imath})+ (y_2\,\vec{\jmath})\times(m_2\,v_2\,\vec{\jmath})=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Aplicaci%C3%B3n:_Dos_muelles_oscilando_en_direcciones_perpendiculares"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 19:52, 21 jul 2010. - Esta página ha sido visitada 3.496 veces. - Aviso legal - Acerca de Laplace