Entrar Página Discusión Historial Go to the site toolbox

Aplicación:Campo de fuerzas paralelas sobre una varilla

De Laplace

Contenido

1 Enunciado

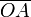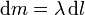Una barra rígida \overline{OA} de longitud L se dispone horizontalmente. Cada punto de la barra tiene una masa infinitesimal \mathrm{d} m=\lambda\,\mathrm{d} l, y una aceleración cuyo módulo es proporcional a la distancia que lo separa de su extremo derecho (con constante de proporcionalidad C), y cuya dirección es perpendicular a la barra y con sentido hacia arriba. Calcula la resultante, el momento resultante respecto de O y el punto central G del sistema de vectores deslizantes paralelos que forman las fuerzas infinitesimales que actúan sobre los puntos de la barra.

2 Solución

2.1 Construcción del vector en cada punto de la barra

El sistema de vectores deslizantes está compuesto por cada uno de los vectores que se asigna a cada uno de los puntos de la barra. En cada punto el vector es 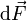\mathrm{d}\vec{F} , que se construye de la siguiente manera.

Escogemos un sistema de ejes de modo que el eje X coincide con la barra, el eje Y es perpendicular a ella apuntando hacia arriba, y el origen coincide con el punto O, el extremo izquierdo de la barra. En cada punto P de la barra el vector es la fuerza que actúa sobre el elemento de línea situado en ese punto. Utilizando la Segunda Ley de Newton, la fuerza sobre cada elemento de línea es el producto de su masa por su aceleración. Llamando 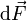\mathrm{d}\vec{F} a esta fuerza, en cada elemento de línea se tiene

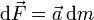
\mathrm{d}\vec{F} = \vec{a}\,\mathrm{d}m

Aquí, dm es la masa del elemento de línea y \vec{a} es la aceleración del elemento.

Según el enunciado, la masa de cada elemento es 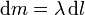\mathrm{d}m=\lambda\,\mathrm{d}l , donde dl es la longitud del elemento de línea y λ es una constante.

Por otro lado, el enunciado dice que la aceleración es perpendicular a la barra, apuntando hacia arriba y con un módulo proporcional a la distancia del punto de la barra a su extremo derecho (con constante de proporcionalidad C). Esto se puede resumir en la siguiente expresión

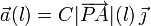
\vec{a}(l) = C|\overrightarrow{PA}|(l)\,\vec{\jmath}

El vector 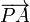\overrightarrow{PA} puede escribirse como

\overrightarrow{PA} = (L-l)\,\vec{\imath} \qquad \qquad \mathrm{con}\,0\leq l \leq L

Para cada valor de l entre 0 y L tenemos un punto distinto de la barra. Con esto, la aceleración en cada punto de la barra es

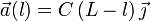
\vec{a}(l) = C\,(L-l)\,\vec{\jmath}

Y la fuerza en cada elemento de línea es

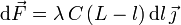
\mathrm{d}\vec{F} = \lambda\,C\,(L-l)\,\mathrm{d}l\,\vec{\jmath}

En un sistema de vectores deslizantes paralelos, cada vector se puede expresar como el producto de un número (con signo) por un vector de módulo unidad que indique la dirección de las rectas soporte de los vectores (vector \vec{u} ). En este caso, escogiendo como vector \vec{u} el vector \vec{\jmath} , esta expresión queda

\mathrm{d}\vec{F} = \mathrm{d}c(l)\,\vec{\jmath} \qquad \mathrm{con}\qquad \mathrm{d}c(l) = \lambda\,C\,(L-l)\,\mathrm{d}l

2.2 Resultante

La resultante es suma vectorial de todos los vectores del sistema considerados como vectores libres. En este caso, hay infinitos elementos de línea, cada un de ellos un diferencial. Por tanto, el sumatorio se convierte en una integral. La resultante es

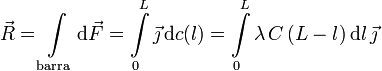
\vec{R} = \int\limits_{\mathrm{barra}}\mathrm{d}\vec{F} = \int\limits_0^L\vec{\jmath}\,\mathrm{d}c(l) = \int\limits_0^L\lambda\,C\,(L-l)\,\mathrm{d}l\,\vec{\jmath}

Al variar l, tanto λ como C y \vec{\jmath} no cambian, por lo que pueden salir de la integral. Tenemos

\vec{R} = \vec{\jmath}\,\lambda\,C\, \int\limits_0^L(L-l)\,\mathrm{d} = \frac{1}{2}\lambda\,C\,L^2\,\vec{\jmath} = R\,\vec{\jmath}

donde

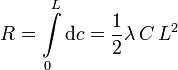
R = \int\limits_0^L\mathrm{d}c =\frac{1}{2}\lambda\,C\,L^2

2.3 Momento resultante respecto a O

Para cada uno de los vectores 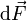\mathrm{d}\vec{F} del sistema, su momento respecto al extremo izquierdo de la barra es

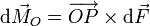
\mathrm{d}\vec{M}_O = \overrightarrow{OP}\times\mathrm{d}\vec{F}

Como se ve en la figura el vector \overrightarrow{OP} es

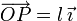
\overrightarrow{OP} = l\,\vec{\imath}

Por tanto, el momento de cada uno de los vectores es

\overrightarrow{OP}\times\mathrm{d}\vec{F} = \left[l\,\vec{\imath}\right]\times\left[\lambda\,C\,(L-l)\,\mathrm{d}l\,\vec{\jmath}\, \right] = \vec{k}\,\lambda\,C\,l(L-l)\mathrm{d}l

El momento resultante del sistema es la suma de estos momentos. De nuevo, al tratarse de diferenciales el sumatorio se transforma en integral. Tenemos

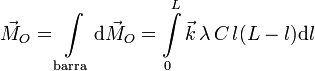
\vec{M}_O = \int\limits_{\mathrm{barra}}\mathrm{d}\vec{M}_O= \int\limits_0^L\vec{k}\,\lambda\,C\,l(L-l)\mathrm{d}l

De nuevo podemos sacar de la integral los elementos que no dependen de la posición del punto P, esto es, de l. El resultado es

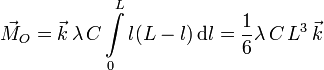
\vec{M}_O = \vec{k}\,\lambda\,C\int\limits_0^Ll(L-l)\,\mathrm{d}l = \frac{1}{6}\lambda\,C\,L^3\,\vec{k}

2.4 Punto central del sistema

La posición del punto central del sistema respecto de un punto genérico O se calcula con la expresión

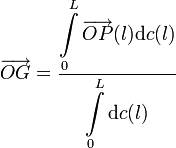
\overrightarrow{OG} = \frac{\displaystyle\int\limits_0^L\overrightarrow{OP}(l)\mathrm{d}c(l)}{\displaystyle\int\limits_0^L\mathrm{d}c(l)}

El denominador lo tenemos del cálculo de la resultante

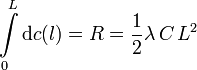
\int\limits_0^L\mathrm{d}c(l) = R = \frac{1}{2}\lambda\,C\,L^2

El numerador es

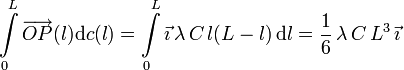
\int\limits_0^L\overrightarrow{OP}(l)\mathrm{d}c(l) = \int\limits_0^L \vec{\imath}\,\lambda\,C\,l(L-l)\,\mathrm{d}l = \frac{1}{6}\,\lambda\,C\,L^3\,\vec{\imath}

Así pues, la posición del punto central viene dada por el vector

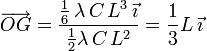
\overrightarrow{OG} = \frac{\frac{1}{6}\,\lambda\,C\,L^3\,\vec{\imath} }{\frac{1}{2}\lambda\,C\,L^2} = \frac{1}{3}L\,\vec{\imath}

El punto central está más cerca del extremo izquierdo que del derecho. Esto es lógico pues, como se ve en la figura, los vectores son mayores cuanto más cerca estamos del extremo izquierdo.

Obtenido de "http://tesla.us.es/wiki/index.php/Aplicaci%C3%B3n:Campo_de_fuerzas_paralelas_sobre_una_varilla"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 20:26, 1 feb 2010. - Esta página ha sido visitada 3.426 veces. - Aviso legal - Acerca de Laplace