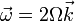Anilla ensartada en dos varillas (CMR)
De Laplace
Contenido |
1 Enunciado
Una pequeña anilla P se encuentra ensartada en la intersección de dos barras giratorias. \ellos extremos fijos de las barras distan una cantidad 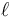 y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:
y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:
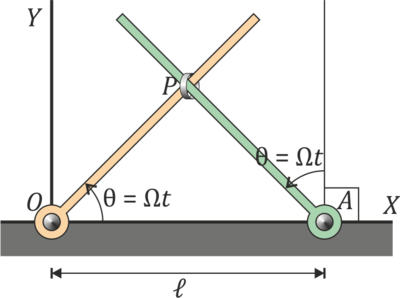
- ¿Cuáles son las ecuaciones horarias de P?
- ¿Qué clase de trayectoria describe?
- ¿Qué tipo de movimiento realiza?
2 Ecuaciones horarias
2.1 Método 1: ángulo en P
La forma más directa de obtener las ecuaciones horarias es observando que el ángulo que forman las dos varillas en P es recto.
Para ver que es así, notamos que el ángulo que la varilla de la derecha forma con el sentido negativo del eje OX es el complementario de θ, esto es
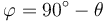
Por otro lado, como los ángulos de un triángulo suman π, el ángulo β que forman las varillas en P es igual a
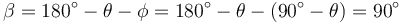
Una vez que sabemos que se trata de un triángulo rectángulo, la obtención de las ecuaciones horarias es inmediata.
La distancia 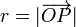 es el cateto contiguo del triángulo, respecto al ángulo en O, por tanto
es el cateto contiguo del triángulo, respecto al ángulo en O, por tanto
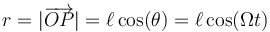
Una vez que tenemos esta distancia, proyectamos sobre los ejes cartesianos, para obtener las dos coordenadas
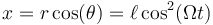
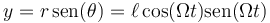
o, en forma vectorial,
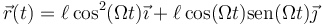
2.2 Método 2: cálculo de las coordenadas
Supongamos que la idea de medir el ángulo en P no es inmediata, ¿no pueden hallarse las ecuaciones horarias de una manera más sistemática? Por supuesto que sí. Sean x e y las coordenadas cartesianas del punto P, r(t) la distancia entre O y P (variable) y b la distancia entre A y P (también variable). Se cumple

Si tomamos la base y la altura del triángulo se cumple

Multiplicando la primera ecuación por el coseno, la segunda por el seno y sumando queda
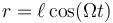
y una vez que tenemos r(t) tenemos las ecuaciones horarias:
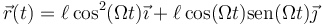
3 Trayectoria
Una vez que tenemos las ecuaciones horarias, ya poseemos una parametrización de la trayectoria (usando el tiempo como variable). No obstante, es de interés el determinar si esta trayectoria posee una ecuación reconocible.
3.1 Método 1: Arco capaz
Una vez que se sabe que el ángulo que forman las varillas en P es recto, es inmediato que la trayectoria es circular. Tal como se ve en el problema del arco capaz, cuando tenemos dos segmentos  y
y 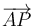 que son siempre perpendiculares en P, entonces, si C es el punto medio entre O y A, la distancia entre C y P cumple
que son siempre perpendiculares en P, entonces, si C es el punto medio entre O y A, la distancia entre C y P cumple
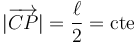
y por tanto P describe un movimiento circular sobre una circunferencia de radio 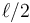 centrada en C, el punto medio de O y A
centrada en C, el punto medio de O y A
3.2 Método 2: Ecuaciones implícitas
Si no se conocen las propiedades de un arco capaz, puede identificarse la trayectoria obteniendo unas ecuaciones implícitas de ella a partir de las ecuaciones horarias
Tenemos en primer lugar que la trayectoria es plana, ya que la anilla se encuentra en todo momento en el plano OXY, esto es,
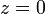
Vimos anteriormente que la distancia OP cumple
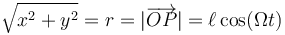
y que las coordenadas cartesianas del punto P valen
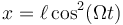
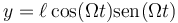
Entonces es inmediato que
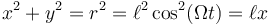
La ecuación
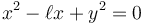
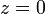
representa una circunferencia en el plano OXY en el que se encuentra la partícula. Obtenemos su centro y su radio completando cuadrados
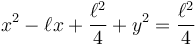

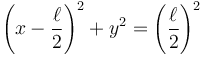
por lo que el centro de la circunferencia y su radio son
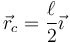
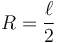
Por tanto, como dijimos, el punto P describe un movimiento circular de centro C y radio 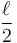 .
.
3.3 Método 3: Radio de curvatura
Si no se conocen ni las propiedades del arco capaz, ni se han hallado ecuaciones implícitas, puede también determinarse que el movimiento es circular estableciendo que el movimiento es plano y que su radio de curvatura es constante.
Que la trayectoria es plana es inmediato de que la anilla se encuentre limitada al plano OXY
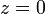
Para hallar el radio de curvatura, según la fórmula
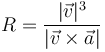
calculamos en primer lugar la velocidad
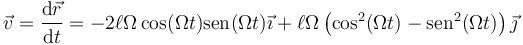
Usando las funciones trigonométricas del ángulo doble esto se simplifica a
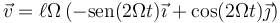
La rapidez de este movimiento es
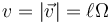
que es una cantidad constante, por lo que el movimiento es uniforme.
Hallamos la aceleración derivando la velocidad respecto al tiempo
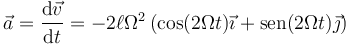
Calculamos el producto vectorial de la velocidad y la aceleración
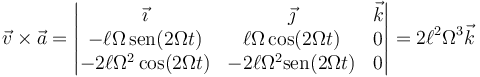
lo que nos da el radio de curvatura
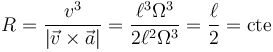
Tenemos entonces que la partícula describe una trayectoria plana con radio de curvatura constante. Por tanto, su movimiento es circular.
4 Tipo de movimiento
Según hemos dicho, la velocidad la calculamos derivando el vector de posición respecto al tiempo
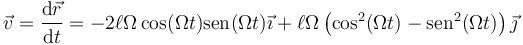
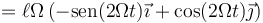
La rapidez de este movimiento es
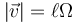
que por ser constante, define este movimiento como uniforme.
Por tanto, la anilla describe un movimiento circular uniforme en el plano OXY, con centro en el punto medio entre los puntos de anclaje de las dos varillas y radio la mitad de la distancia entre estos dos puntos
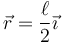
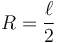
A partir de la expresión para la velocidad en un movimiento circular
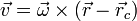
se obtiene que la velocidad angular de este movimiento es