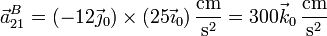5.4. Bola en canal circular
De Laplace
Contenido |
1 Enunciado
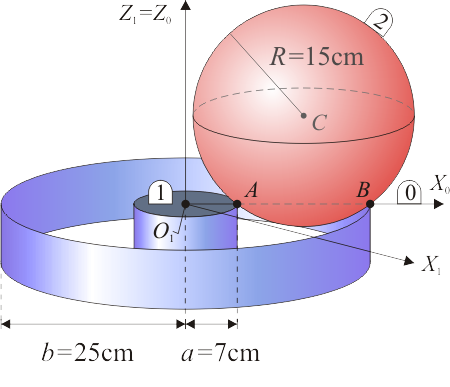
Una bola (sólido “2”), de radio 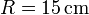 , se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios
, se desplaza sobre dos carriles circulares concéntricos fijos (sólido “1”), de radios 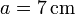 y
y 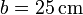 , situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que:
, situados en un plano horizontal (ver figura). El movimiento de esta esfera es tal que:
- en todo instante, rueda sin deslizar sobre ambos carriles, y
- su centro C realiza un movimiento circular uniforme con celeridad
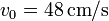 y en sentido antihorario respecto al eje O1Z1.
y en sentido antihorario respecto al eje O1Z1.
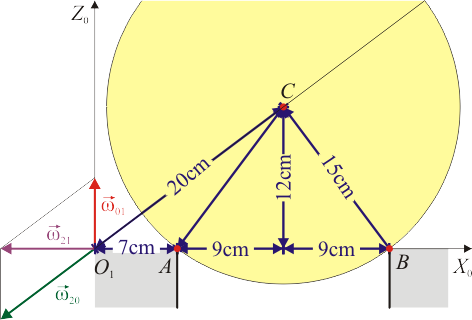
Consideramos como sólido móvil intermedio (sólido 0) al plano O1X0Z0 que contiene en todo instante al centro C de la esfera (ver figura).
- Halle los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
- Halle la reducción cinemática canónica de cada movimiento.
- Para el punto de la pelota en contacto con el carril de mayor radio (punto B), determine
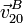 y
y  .
.
2 Ejes de rotación
- Movimiento {21}
- El eje del movimiento {21} es fácil de identificar. Puesto que los puntos A y B están en reposo instantáneo en este movimiento, la recta que pasa por ellos es un eje instantáneo de rotación (EIR). No es un eje permanente, pues la posición de los puntos A y B en el sistema de referencia “1” va cambiando en el tiempo.
- Movimiento {01}
- Por ser coincidentes los ejes O1Z0 y O1Z1, cualquier punto del eje O1Z0, perteneciente al sólido 0, se encuentra en reposo respecto al sólido 1, por lo que este es un eje de rotación. Puesto que el eje es fijo en el triedro 1, se trata de un eje permanente de rotación.
- Movimiento {20}
- En este también podemos identificar dos puntos fijos. Uno es el origen común del sistema de ejes O1. El otro es el centro de la esfera, C, que se encuentra situado siempre a la misma distancia de los ejes en el plano O1X0Z0. Se trata de un eje permanente de rotación, ya que la recta que pasa por los puntos O1 y C ocupa una posición fija en el triedro 0.
3 Reducciones de los movimientos
3.1 Movimiento {01}
Según hemos dicho, el movimiento del sólido 0 es una rotación permanente alrededor del eje O1Z1. La velocidad angular de este movimiento es de la forma
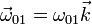
El módulo de esta velocidad angular lo obtenemos de que conocemos la rapidez del punto C y su distancia al eje O1Z1
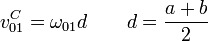

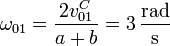
La velocidad de deslizamiento en este movimiento es nula, por tratarse de una rotación pura.
3.2 Movimiento {21}
El movimiento {21} es también una rotación pura, por lo que su velocidad de deslizamiento es nula. La velocidad angular de este movimiento va en la dirección de la recta que pasa por A y B, que es el eje O1X0. Por ello
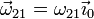
El valor de esta componente lo obtenemos también de que conocemos la velocidad de C en este movimiento, ya que es igual a la anterior
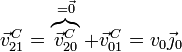
Tomando módulos
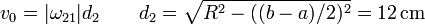

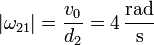
El sentido de la velocidad angular lo da la regla de la mano derecha, según la cual
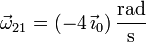
Alternativamente, puede hallarse este vector a partir de la relación
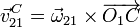
con
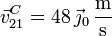
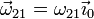
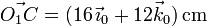
3.3 Movimiento {20}
El movimiento relativo es también una rotación, por tener al menos un punto fijo (el origen común). La velocidad de deslizamiento de este sólido es nula. La velocidad angular la podemos obtener a partir de las que ya tenemos
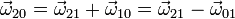
Sustituyendo los valores numéricos
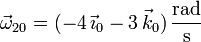
Este vector apunta en la dirección de la recta que pasa por 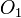 y
y  , que identificamos
anteriormente como la del eje instantáneo de rotación.
, que identificamos
anteriormente como la del eje instantáneo de rotación.
4 Velocidad y aceleración
4.1 Velocidad
En el movimiento {20} el punto B experimenta una rotación instantánea en torno al eje que
pasa por 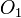 y
y  . Por ello, su velocidad es
. Por ello, su velocidad es
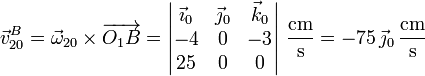
A este misma vector se puede llegar hallando la rapidez simplemente multiplicando el módulo de la velocidad angular por la distancia de B al EIR

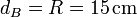
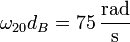
y asignando la dirección y el sentido según la regla de la mano derecha.
4.2 Aceleración
La aceleración del punto B en el movimiento absoluto {21} la podemos obtener aplicando la expresión del campo de aceleraciones de un sólido
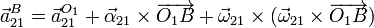
La aceleración 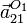 es nula, por tratarse
es nula, por tratarse 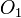 de un punto fijo. También se
anula el último término, ya que por estar
de un punto fijo. También se
anula el último término, ya que por estar 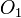 y
y  en el EIR del movimiento {21}, el vector
de posición relativo es paralelo a la velocidad angular. La aceleración se reduce
entonces a
en el EIR del movimiento {21}, el vector
de posición relativo es paralelo a la velocidad angular. La aceleración se reduce
entonces a
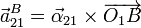
La aceleración angular del movimiento absoluto la calculamos como composición del movimiento relativo y del de arrastre
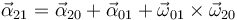
La aceleraciones angulares relativa y de arrastre son las dos nulas, por tratarse de sendas rotaciones sobre ejes permanentes a velocidad angular constante.
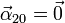
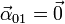
Queda entonces
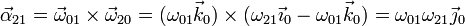
Sustituyendo los valores numéricos
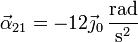
y llevando esto a la ecuación de la aceleración del punto B