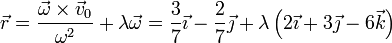4.2. Ejemplo de campo de velocidades de un sólido
De Laplace
Contenido |
1 Enunciado
Un campo de velocidades de un sistema de partículas tiene la expresión, en el SI,
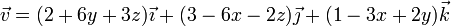
- Pruebe que corresponde al movimiento de un sólido rígido.
- Determine la velocidad angular y la velocidad de deslizamiento.
- Halle la ecuación del eje instantáneo de rotación y mínimo deslizamiento.
2 Velocidad de un sólido rígido
Para probar que corresponde a un posible movimiento de un sólido rígido, lo más directo es usar la condición cinemática de rigidez, esto es, probar que el campo de velocidades es equiproyectivo. Esto se puede escribir en la forma

Consideramos dos puntos arbitrarios
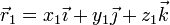
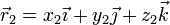
con velocidades
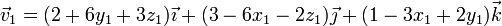
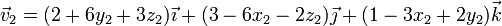
Hallamos la posición relativa
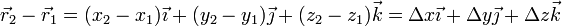
y la velocidad relativa
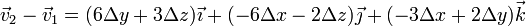
Calculamos su producto escalar
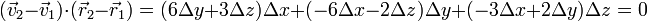
Por tanto el campo es equiproyectivo y corresponde al movimiento de un sólido rígido.
3 Velocidad angular y de deslizamiento
3.1 Velocidad angular
Podemos hallar la velocidad angular del movimiento simplemente comparando la expresión del enunciado con la expresión general
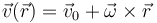
Sustituyendo la expresión en componentes cartesianas
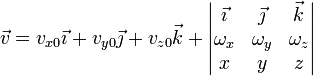
Desarrollando e igualando nos queda

Dado que esto se cumple para todo x, y y z debe ser

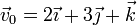
3.2 Velocidad de deslizamiento
La velocidad de deslizamiento es la proyección de la velocidad de cualquier punto en la dirección de la velocidad angular. La obtenemos mediante el producto escalar por el vector unitario en dicha dirección. Este vector unitario es

resultando la velocidad de deslizamiento
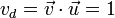
Y el vector velocidad de deslizamiento se obtiene multiplicando por el unitario en la dirección de la velocidad angular
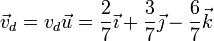
4 EIRMD
Podemos obtener la posición del EIRMD empleando la fórmula general fórmula general