3.2. Partícula sometida a fuerza dependiente de una coordenada (Ex.Ene/11)

De Laplace

Contenido

1 Enunciado
2 Integración de las ecuaciones de movimiento
3 Integral primera
- 3.1 Derivando G
- 3.2 Sustituyendo las ecuaciones horarias

1 Enunciado

Una partícula material de masa $m$ parte del origen de coordenadas con velocidad 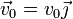$\vec{v}_0=v_0\vec{\jmath}$ , encontrándose sometida en todo momento a la fuerza dependiente de la posición

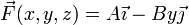
$\vec{F}(x,y,z)=A\vec{\imath}-By\vec{\jmath}$

siendo 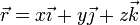$\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$ la posición instantánea de la partícula, y $A$ y $B$ dos constantes positivas conocidas.

Calcule la posición, velocidad y aceleración instantáneas de la partícula para todo instante de tiempo, $t$ .
Demuestre que

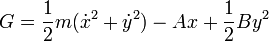
$G = \frac{1}{2}m(\dot{x}^2+\dot{y}^2)-Ax+\frac{1}{2}By^2$

es una integral primera del movimiento de la partícula y calcule su valor en todo instante. ¿Qué significado físico tiene esta cantidad?

2 Integración de las ecuaciones de movimiento

Debemos determinar la posición de la partícula en cada instante, conocida la fuerza que actúa sobre ella. Nuestro punto de partida es la segunda ley de Newton

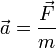
$\vec{a}=\frac{\vec{F}}{m}$

con las condiciones iniciales

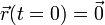
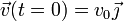
$\vec{r}(t=0) = \vec{0}$ $\vec{v}(t=0)=v_0\vec{\jmath}$

Escribimos la segunda ley en la base canónica. Para ello, aplicamos que las componentes cartesianas de la aceleración son las segundas derivadas de las coordenadas cartesianas del punto

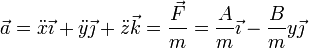
$\vec{a}=\ddot{x}\vec{\imath}+\ddot{y}\vec{\jmath}+\ddot{z}\vec{k}=\frac{\vec{F}}{m}=\frac{A}{m}\vec{\imath}-\frac{B}{m}y\vec{\jmath}$

Igualando componente a componente:

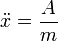
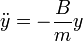
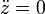
$\ddot{x}=\frac{A}{m}$ $\ddot{y}=-\frac{B}{m}y$ $\ddot{z}=0$

Cada una de estas ecuaciones se puede resolver por separado. Las condiciones iniciales para cada una son, de la posición inicial

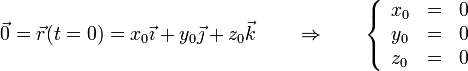
$\vec{0}=\vec{r}(t=0)=x_0\vec{\imath}+y_0\vec{\jmath}+z_0\vec{k}\qquad\Rightarrow\qquad\left\{\begin{array}{lcr} x_0 & = & 0 \\ y_0 & = & 0 \\ z_0 & = & 0 \end{array}\right.$

y de la velocidad inicial:

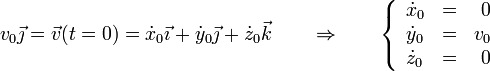
$v_0\vec{\jmath}=\vec{v}(t=0)=\dot{x}_0\vec{\imath}+\dot{y}_0\vec{\jmath}+\dot{z}_0\vec{k}\qquad\Rightarrow\qquad\left\{\begin{array}{lcr} \dot{x}_0 & = & 0 \\ \dot{y}_0 & = & v_0 \\ \dot{z}_0 & = & 0 \end{array}\right.$

Resolvemos componente a componente:

Componente x: La primera componente satisface

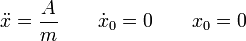
$\ddot{x}=\frac{A}{m}\qquad\dot{x}_0=0\qquad x_0=0$

Esta es la ecuación de un movimiento uniforme acelerado. Obtenemos la coordenada

x

como función del tiempo integrando dos veces respecto al tiempo. La primera integración nos da la componente x de la velocidad:

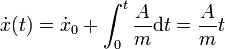
$\dot{x}(t)=\dot{x}_0+\int_0^t \frac{A}{m}\mathrm{d}t = \frac{A}{m}t$

y la segunda la de la posición

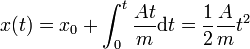
$x(t) = x_0+\int_0^t \frac{At}{m}\mathrm{d}t=\frac{1}{2}\frac{A}{m}t^2$

Podíamos haber llegado directamente a este resultado simplemente sustituyendo las ecuaciones del movimiento uniformemente acelerado en una dimensión.

Componente y: La ecuación para la segunda componente es

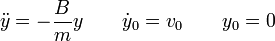
$\ddot{y}=-\frac{B}{m}y\qquad\dot{y}_0=v_0\qquad y_0=0$

Esta es la ecuación de un oscilador armónico de frecuencia natural

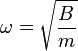
$\omega = \sqrt{\frac{B}{m}}$

La integración de este movimiento da una sinusoide

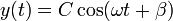
$y(t) = C \cos(\omega t+\beta)\,$

siendo

C

y

β

dos constantes que imponemos de las condiciones iniciales

$0 = y_0 = C\cos(\beta)\qquad\qquad v_0 = \dot{y}_0 = -C\omega\,\mathrm{sen}(\beta)$

De la primera obtenemos que

β = π / 2

y, sustituyendo en la segunda,

C = - v 0 / ω

. Por tanto la dependencia de y respecto al tiempo es

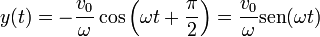
$y(t) = -\frac{v_0}{\omega}\cos\left(\omega t+\frac{\pi}{2}\right)=\frac{v_0}{\omega}\mathrm{sen}(\omega t)$

Componente z: Por último tenemos

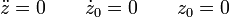
$\ddot{z}=0\qquad\dot{z}_0=0\qquad z_0=0$

Esta ecuación es idéntica a la de la componente x, con la simplificación adicional de que la aceleración es nula, resultando simplemente

z (t) = 0

Reuniendo los tres resultados obtenemos las ecuaciones horarias

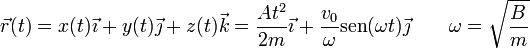
$\vec{r}(t)=x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}=\frac{At^2}{2m}\vec{\imath}+\frac{v_0}{\omega}\mathrm{sen}(\omega t)\vec{\jmath}\qquad \omega = \sqrt{\frac{B}{m}}$

Derivando una vez respecto al tiempo obtenemos la velocidad

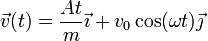
$\vec{v}(t)=\frac{At}{m}\vec{\imath}+v_0\cos(\omega t)\vec{\jmath}$

y derivando una segunda vez hallamos la aceleración

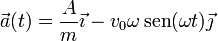
$\vec{a}(t)=\frac{A}{m}\vec{\imath}-v_0\omega\,\mathrm{sen}(\omega t)\vec{\jmath}$

3 Integral primera

Para demostrar que G es una integral primera tenemos dos caminos directos:

Derivar G y comprobar que la derivada es nula en todo instante.
Sustituir la solución anterior y ver que sale un valor constante.

3.1 Derivando G

Si elegimos el primer camino, porque no requiere haber resuelto el primer apartado, tenemos

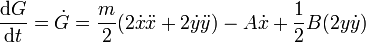
$\frac{\mathrm{d}G}{\mathrm{d}t}=\dot{G}=\frac{m}{2}(2\dot{x}\ddot{x}+2\dot{y}\ddot{y})-A\dot{x}+\frac{1}{2}B(2y\dot{y})$

Agrupando términos

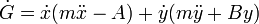
$\dot{G}=\dot{x}(m\ddot{x}-A)+\dot{y}(m\ddot{y}+By)$

Si aquí sustituimos la segunda ley de Newton queda

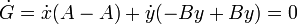
$\dot{G}=\dot{x}(A-A)+\dot{y}(-By+By)=0$

y por tanto G es una integral primera o constante de movimiento. Su valor los obtenemos sustituyendo las condiciones iniciales

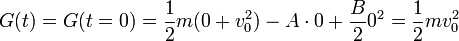
$G(t) = G(t=0) = \frac{1}{2}m(0+v_0^2) -A\cdot 0+\frac{B}{2}0^2 = \frac{1}{2}mv_0^2$

En cuanto a su interpretación física es sencilla. El primer término es la energía cinética

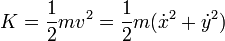
$K = \frac{1}{2}mv^2= \frac{1}{2}m(\dot{x}^2+\dot{y}^2)$

y el segundo es la suma de la energía potencial asociada a una fuerza constante (como el peso), mientras que la segunda es la energía potencial de un oscilador armónico

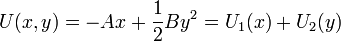
$U(x,y) = -Ax + \frac{1}{2}By^2 = U_1(x) + U_2(y)$

Concluimos entonces que la cantidad G no es otra que la energía mecánica de la partícula

$G = K + U = E\,$

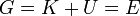
3.2 Sustituyendo las ecuaciones horarias

Si optamos por sustituir la solución calculada en el primer apartado, obtenemos

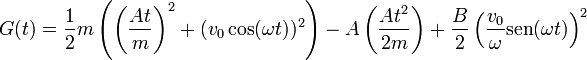
$G(t) = \frac{1}{2}m\left(\left(\frac{At}{m}\right)^2+(v_0\cos(\omega t))^2\right)-A\left(\frac{At^2}{2m}\right)+\frac{B}{2}\left(\frac{v_0}{\omega}\mathrm{sen}(\omega t)\right)^2$

Agrupando términos

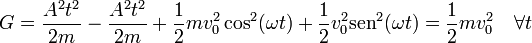
$G = \frac{A^2t^2}{2m}-\frac{A^2t^2}{2m}+\frac{1}{2}mv_0^2\cos^2(\omega t) + \frac{1}{2}v_0^2\mathrm{sen}^2(\omega t) = \frac{1}{2}mv_0^2\quad \forall t$

y por tanto $G$ es constante.

3.2. Partícula sometida a fuerza dependiente de una coordenada (Ex.Ene/11)

De Laplace

Contenido

1 Enunciado

2 Integración de las ecuaciones de movimiento

3 Integral primera

3.1 Derivando G

3.2 Sustituyendo las ecuaciones horarias

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES