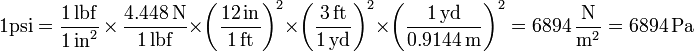Entrar Página Discusión Historial Go to the site toolbox

1.7. Ejemplos de conversión de unidades

De Laplace

Contenido

1 Enunciado

Exprese estas cantidades en términos de las unidades fundamentales del SI:

  1. Nudo (milla náutica/hora)
  2. Año luz
  3. Acre (rectángulo de 66 pies por 220 yardas)
  4. Siglo
  5. Unidad de Masa Atómica
  6. R = 0.082 atm·L/K·mol
  7. Libra-fuerza por pulgada cuadrada (Ex.Ene/11)

2 Nudo

Un nudo, unidad de velocidad para naves (barcos o aviones) se define como una milla náutica (M) por hora. A su vez, una milla náutica se define como el arco correspondiente a un minuto de grado sobre la superficie terrestre.

Si en una circunferencia hay 360° y cada uno contiene 60 minutos de arco ('), se deduce que hay

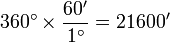
360^\circ\times \frac{60'}{1^\circ} = 21600'

Dado que la circunferencia terrestre mide 40000 km (por la definición original de metro), tenemos que cada minuto corresponde a un arco

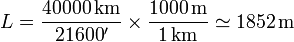
L = \frac{40000\,\mathrm{km}}{21600'}\times\frac{1000\,\mathrm{m}}{1\,\mathrm{km}}\simeq 1852\,\mathrm{m}

El cociente incluye decimales, pero la Oficina Internacional de Pesas y Medidas define la milla náutica como exactamente 1852 metros.

Un nudo (kn) corresponde por tanto a

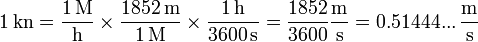
1\,\mathrm{kn} = \frac{1\,\mathrm{M}}{\mathrm{h}}\times\frac{1852\,\mathrm{m}}{1\,\mathrm{M}}\times\frac{1\,\mathrm{h}}{3600\,\mathrm{s}} = \frac{1852}{3600}\frac{\mathrm{m}}{\mathrm{s}}= 0.51444...\,\frac{\mathrm{m}}{\mathrm{s}}

3 Año luz

El año luz es una unidad de longitud, equivalente a la distancia recorrida por la luz en un año. La velocidad de la luz es exactamente

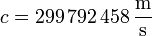
c = 299\,792\,458\,\frac{\mathrm{m}}{\mathrm{s}}

La duración del año es un poco más incierta, ya que no es un múltiplo exacto de un número de días (d). Para definir un año luz se toma un año de 365.25 d (que tiene en cuenta los años bisiestos, pero no la corrección de la reforma gregoriana; el año solar real dura un poco menos de 365.25 d). Con esta definición de años obtenemos

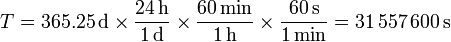
T = 365.25\,\mathrm{d}\times\frac{24\,\mathrm{h}}{1\,\mathrm{d}}\times\frac{60\,\mathrm{min}}{1\,\mathrm{h}}\times\frac{60\,\mathrm{s}}{1\,\mathrm{min}}=31\,557\,600\,\mathrm{s}

por lo que la longitud de un año luz es

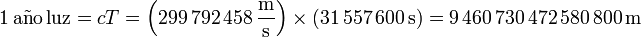
1\,\mathrm{a}\tilde{\mathrm{n}}\mathrm{o\,luz} = cT = \left(299\,792\,458\,\frac{\mathrm{m}}{\mathrm{s}}\right)\times\left(31\,557\,600\,\mathrm{s}\right) = 9\,460\,730\,472\,580\,800\,\mathrm{m}

esto es, un año luz es un poco menos de 10 billones de kilómetros. Normalmente, con esta cantidad redondeada es más que suficiente para expresar las distancias estelares, por las incertidumbres inherentes a las medidas astronómicas.

4 Acre

Un acre es una medida de superficie, relacionado con una cierta cantidad de superficie arable, de ahí su definición empleando un rectángulo. Los lados de este rectángulo se miden en yardas y pies, que son unidades del sistema imperial de unidades.

Una yarda (yd) se define como

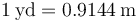
1\,\mathrm{yd} = 0.9144\,\mathrm{m}

y una yarda contiene 3 pies (ft), por lo que

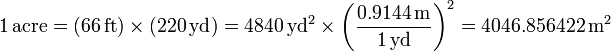
1\,\mathrm{acre} = (66\,\mathrm{ft})\times(220\,\mathrm{yd}) = 4840\,\mathrm{yd}^2 \times \left(\frac{0.9144\,\mathrm{m}}{1\,\mathrm{yd}}\right)^2 = 4046.856422\,\mathrm{m}^2

esto es, un acre equivale aproximadamente a 0.4 hectáreas (1 ha = 10000 m²).

5 Siglo

Un siglo es una unidad de tiempo equivalente a 100 años. La duración de un año es, aproximadamente 365 días más 1/4 (el año Juliano). Una mejor aproximación la da el año Gregoriano, que elimina tres años bisiestos cada cuatrocientos años, esto es

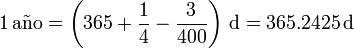
1\,\mathrm{a}\tilde{\mathrm{n}}\mathrm{o} = \left(365 + \frac{1}{4}-\frac{3}{400}\right)\,\mathrm{d}=365.2425\,\mathrm{d}

Por tanto, un siglo equivale a

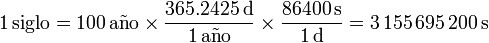
1\,\mathrm{siglo} = 100\,\mathrm{a}\tilde{\mathrm{n}}\mathrm{o}\times\frac{365.2425\,\mathrm{d}}{1\,\mathrm{a}\tilde{\mathrm{n}}\mathrm{o}}\times\frac{86400\,\mathrm{s}}{1\,\mathrm{d}} = 3\,155\,695\,200\,\mathrm{s}

Una buena aproximación sería decir que un siglo son

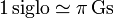
1\,\mathrm{siglo} \simeq \pi\,\mathrm{Gs}

6 Unidad de Masa Atómica

La Unidad de Masa Atómica Unificada (u), también conocida como dalton (Da) se define como 1/12 de la masa de un átomo de 12C. Puesto que 1 mol de esta misma sustancia pesa 12 gramos y en 1 mol hay el Número de Avogadro de partículas, siendo

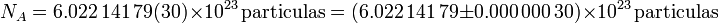
N_A = 6.022\,141\,79(30)\times 10^{23}\,\mathrm{particulas} = (6.022\,141\,79\pm 0.000\,000\,30)\times 10^{23}\,\mathrm{particulas}

La unidad de masa atómica unificada equivale entonces a

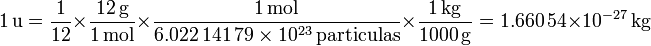
1\,\mathrm{u} = \frac{1}{12}\times\frac{12\,\mathrm{g}}{1\,\mathrm{mol}}\times\frac{1\,\mathrm{mol}}{6.022\,141\,79\times 10^{23}\,\mathrm{particulas}}\times\frac{1\,\mathrm{kg}}{1000\,\mathrm{g}} = 1.660\,54\times 10^{-27}\,\mathrm{kg}

Dado que el número de Avogadro es una cantidad experimental, la Unidad de Masa Atómica, a diferencia de otras unidades, tiene solo un valor aproximado, con una cierta incertidumbre. Su valor actual es

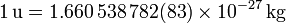
1\,\mathrm{u} = 1.660\,538\,782(83)\times 10^{-27}\,\mathrm{kg}

donde el 83 entre paréntesis representa la incertidumbre en las dos últimas cifras.

7 Constante de los gases ideales

El valor de la constante de los gases ideales en el SI se obtiene transformando las atmósferas a pascales y los litros a m³. Tenemos que

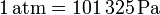
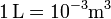
1\,\mathrm{atm} = 101\,325\,\mathrm{Pa}        1\,\mathrm{L}=10^{-3}\mathrm{m}^3

por lo que

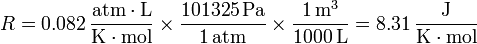
R = 0.082\,\frac{\mathrm{atm}\cdot\mathrm{L}}{\mathrm{K}\cdot\mathrm{mol}}\times\frac{101325\,\mathrm{Pa}}{1\,\mathrm{atm}}\times\frac{1\,\mathrm{m}^3}{1000\,\mathrm{L}} = 8.31\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}

Nótese que en el numerador aparece el julio, ya que

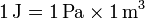
1\,\mathrm{J}=1\,\mathrm{Pa}\times 1\,\mathrm{m}^3

El valor experimental más preciso para R en el SI es

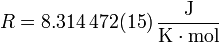
R = 8.314\,472(15)\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}

donde de nuevo el 15 entre paréntesis indica la incertidumbre en las dos ultimas cifras, esto es,

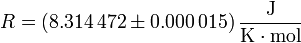
R = (8.314\,472\pm 0.000\,015)\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}

8 Libra-fuerza por pulgada cuadrada

La libra-fuerza por pulgada cuadrada, más conocida como psi (pounds per square inch) es una unidad de presión en el sistema imperial de unidades. Teniendo en cuenta que una libra-fuerza equivale a 4.448 N, que un pie tiene 12 pulgadas, una yarda tiene 3 pies y que una yarda equivale a 0.9144 metros, se obtiene que un psi equivale a

1 \mathrm{psi} = \frac{1\,\mathrm{lbf}}{1\,\mathrm{in}^2}\,\times\,\frac{4.448\,\mathrm{N}}{1\,\mathrm{lbf}}\times\left(\frac{12\,\mathrm{in}}{1\,\mathrm{ft}}\right)^2\times\left(\frac{3\,\mathrm{ft}}{1\,\mathrm{yd}}\right)^2\times\left(\frac{1\,\mathrm{yd}}{0.9144\,\mathrm{m}}\right)^2 = 6894\,\frac{\mathrm{N}}{\mathrm{m}^2} = 6894\,\mathrm{Pa}
Obtenido de "http://tesla.us.es/wiki/index.php/1.7._Ejemplos_de_conversi%C3%B3n_de_unidades"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 20:58, 17 sep 2012. - Esta página ha sido visitada 106.951 veces. - Aviso legal - Acerca de Laplace