Entrar Página Discusión Historial Go to the site toolbox

Preguntas de test de cinemática tridimensional de la partícula (GIE)

De Laplace

(Diferencias entre revisiones)
m (→Pregunta 1)
m (→Pregunta 2)
Línea 554: Línea 554:
En este caso sabemos que la aceleración angular es constante, por lo que la tangencial también lo es
En este caso sabemos que la aceleración angular es constante, por lo que la tangencial también lo es
-
<center><math>a_t = CR\,</math></center>
+
<center><math>a_t = \frac{CR}{2}\,</math></center>
La aceleración normal, en cambio, aumenta al crecer la velocidad angular
La aceleración normal, en cambio, aumenta al crecer la velocidad angular

Revisión de 17:14 19 oct 2018

Contenido

1 Posición de una partícula

La posición de una partícula se describe según las siguientes ecuaciones horarias

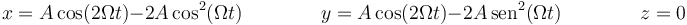
x=A \cos⁡(2\Omega t)-2A \cos^2⁡(\Omega t)\qquad\qquad y=A\cos⁡(2\Omega t)-2A\,\mathrm{sen}^2⁡(\Omega t)\qquad\qquad z=0

¿Qué tipo de movimiento describe la partícula?

  • A Circular.
  • B Parabólico.
  • C Armónico simple.
  • D Está en reposo.
Solución

La respuesta correcta es la C.

2 Movimiento circular

Una partícula describe el movimiento circular de ecuación, en el SI,

\vec{r}(t)=5\cos⁡(5t)\vec{\imath}+3\,\mathrm{sen}⁡(5t)\vec{\jmath}+4\,\mathrm{sen}⁡(5t)\vec{k}

2.1 Pregunta 1

La velocidad angular de este movimiento vale, en rad/s

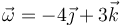  • A \vec{\omega}=-4\vec{\jmath}+3\vec{k}.
  • B 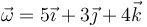\vec{\omega}=5\vec{\imath}+3\vec{\jmath}+4\vec{k}.
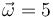  • C \vec{\omega}=5.
  • D 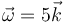\vec{\omega}=5\vec{k}.
Solución

La respuesta correcta es la A.

2.2 Pregunta 2

¿Cuánto vale el radio de este movimiento circular, en m?

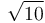  • A \sqrt{10}.
  • B 50.
  • C 5.
  • D No hay información suficiente para determinarlo.
Solución

La respuesta correcta es la C.

3 Vector tangente constante

De un movimiento de una partícula sabemos que el vector tangente es constante. Podemos asegurar que este movimiento es…

  • A Uniforme.
  • B Rectilíneo.
  • C Circular.
  • D Helicoidal.
Solución

La respuesta correcta es la B.

4 Ángulo entre velocidad y aceleración

Una partícula se mueve de forma que en un instante dado su aceleración y su velocidad forman un ángulo de 3π / 4. En ese momento la partícula…

  • A está cambiando su dirección pero manteniendo constante su rapidez.
  • B esta frenando, pero manteniendo su dirección de movimiento.
  • C está frenando y cambiando su dirección.
  • D está acelerando mientras cambia su dirección.
Solución

La respuesta correcta es la C.

La aceleración normal no es nula

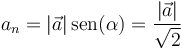
a_n=\left|\vec{a}\right|\mathrm{sen}(\alpha)=\frac{|\vec{a}|}{\sqrt{2}}

por lo que la dirección está cambiando.

También es distinta de cero la aceleración tangencial

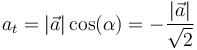
a_t=\left|\vec{a}\right|\mathrm{cos}(\alpha)=-\frac{|\vec{a}|}{\sqrt{2}}

Al ser negativa, quiere decir que la rapidez está disminuyendo y por tanto la partícula está frenando.

5 Movimiento oscilatorio sobre circunferencia

Una partícula se mueve sobre la circunferencia, expresada en polares y en el SI, ρ = 1.00m, siguiendo la ley horaria

\theta = \pi \cos(\pi t)\qquad \forall t

con θ el ángulo que el vector de posición forma con el eje OX positivo.

5.1 Pregunta 1

La aceleración angular en t = (1/3)s vale aproximadamente, en rad/s²,…

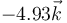
  • A -4.93\vec{k}
  • B -8.54\vec{k}
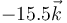
  • C -15.5\vec{k}
  • D +8.54\vec{k}
Solución

La respuesta correcta es la C.

En el caso de un movimiento circular en el plano XY con centro el origen de coordenadas, la aceleración angular es un vector en la dirección del eje OZ y cuya componente vertical es igual a la segunda derivada del ángulo θ respecto al tiempo

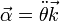
\vec{\alpha}=\ddot{\theta}\vec{k}

En este caso

\vec{\omega} = \dot{\theta}\vec{k}=-\pi^2\mathrm{sen}(\pi t)\vec{k}\qquad\qquad \vec{\alpha} = -\pi^3\cos(\pi t)\vec{k}

En t = (1 / 3)s, su valor es

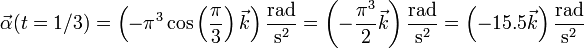
\vec{\alpha}(t=1/3) = \left(-\pi^3\cos\left(\frac{\pi}{3}\right)\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}=\left(-\frac{\pi^3}{2}\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}=\left(-15.5\vec{k}\right)\frac{\mathrm{rad}}{\mathrm{s}^2}

5.2 Pregunta 2

Para este mismo movimiento, la velocidad lineal cuando pasa por θ = 0 es…

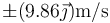  • A \pm(9.86\vec{\jmath})\mathrm{m}/\mathrm{s}.
  • B nula.
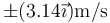  • C \pm (3.14 \vec{\imath})\mathrm{m}/\mathrm{s}.
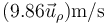  • D (9.86 \vec{u}_\rho)\mathrm{m}/\mathrm{s}.
Solución

La respuesta correcta es la A.

A la respuesta correcta se puede llegar sin hacer ningún cálculo.

Al pasar por el origen la velocidad no es nula, sino máxima como ocurre siempre en el punto de equilibrio de un movimiento oscilatorio. Esto descarta la respuesta B.

Asimismo, la velocidad lineal es siempre tangente a la trayectoria. En θ = 0 la circunferencia tiene tangente vertical, que es la dirección de \vec{\jmath}. Por lo tanto no puede ser correcta la respuesta C ni la D (perpendiculares ambas a la circunferencia).

Esto nos deja solo con la opción A, que es la correcta.

Podemos, no obstante, calcular la velocidad lineal en ese punto.

La velocidad lineal en un movimiento circular la podemos calcular a partir de la velocidad angular y el vector de posición

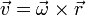
\vec{v}=\vec{\omega}\times\vec{r}

Cuando la partícula pasa por θ = 0 su posición es

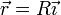
\vec{r}=R\vec{\imath}

por lo que

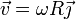
\vec{v}=\omega R\vec{\jmath}

La velocidad lineal, que es siempre tangente a la trayectoria, va en la dirección paralela al eje Y para este punto. No obstante, podría ser nula, por lo que debemos calcular el valor de la velocidad angular.

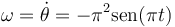
\omega = \dot{\theta}=-\pi^2\mathrm{sen}(\pi t)

La partícula pasa por θ = 0 cuando

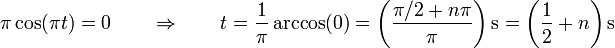
\pi\cos(\pi t) = 0 \qquad\Rightarrow\qquad t = \frac{1}{\pi}\arccos(0) = \left(\frac{\pi/2+ n\pi}{\pi}\right)\mathrm{s}=\left(\frac{1}{2}+n\right)\mathrm{s}

Para estos instantes

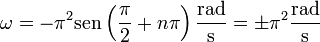
\omega = -\pi^2\mathrm{sen}\left(\frac{\pi}{2}+n\pi\right)\frac{\mathrm{rad}}{\mathrm{s}}=\pm \pi^2\frac{\mathrm{rad}}{\mathrm{s}}

El signo depende del valor de n. Si n es par es negativo, y positivo si es impar. De aquí nos quedan los valores para la velocidad

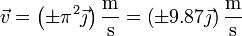
\vec{v}=\left(\pm \pi^2\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}= \left(\pm 9.87\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}}
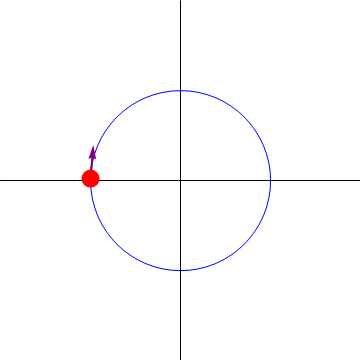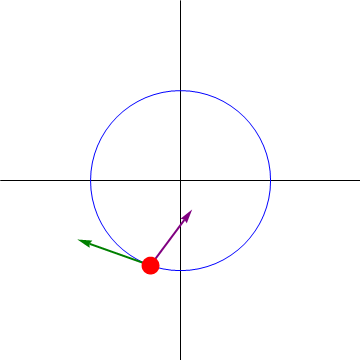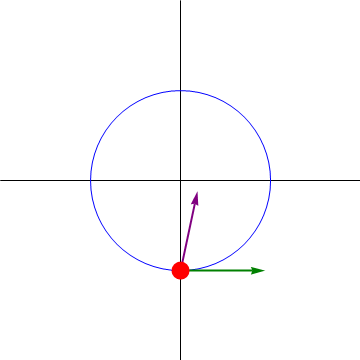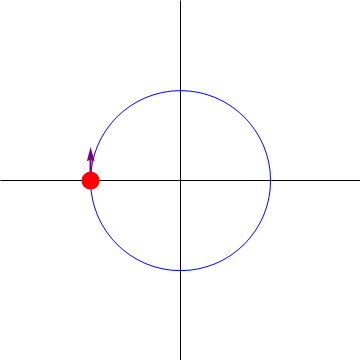
Archivo:movimiento-circular-oscilatorio.gif

Este resultado se puede visualizar observando que el movimiento que realiza la partícula es oscilatorio en la coordenada θ, esto es, es análogo a un movimiento armónico simple, pero sobre una circunferencia en lugar de en línea recta. El punto θ = 0 corresponde al punto central de la oscilación, en el que la velocidad es máxima, pudiendo ir en un sentido o en el opuesto.

5.3 Pregunta 3

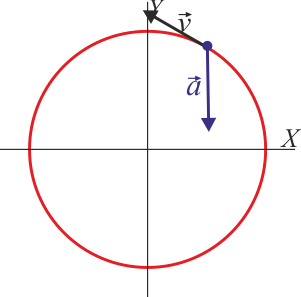
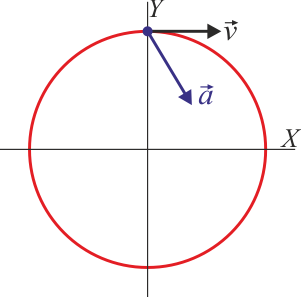
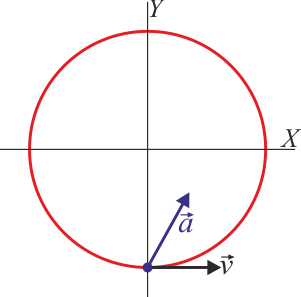
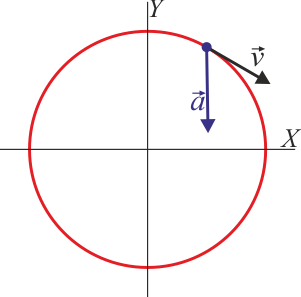
Para el mismo movimiento, indique cuál de las siguientes figuras representa la velocidad y la aceleraciones lineales en t = (1/3)s.

Archivo:va-circular-oscilatorio-01.png Archivo:va-circular-oscilatorio-02.png
A B
Archivo:va-circular-oscilatorio-03.png Archivo:va-circular-oscilatorio-04.png
C D
Solución

La respuesta correcta es la B.

En principio las cuatro figuras corresponden a situaciones posibles del movimiento circular, por lo que sería necesario hallar cuánto vale la velocidad y la aceleración en el instante indicado para discernir entre las cuatro posibilidades.

Sin embargo, no es necesario. Nos basta con determinar la posición en el instante indicado. Cuando 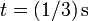t = (1/3)\,\mathrm{s}

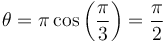
\theta=\pi\cos\left(\frac{\pi}{3}\right)=\frac{\pi}{2}

es decir, la partícula se encuentra en

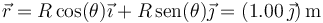
\vec{r}=R\cos(\theta)\vec{\imath}+R\,\mathrm{sen}(\theta)\vec{\jmath}=(1.00\,\vec{\jmath})\,\mathrm{m}

y hay una sola figura correspondiente a esta posición:

Archivo:va-circular-oscilatorio-02.png

Podemos, no obstante, hallar la velocidad y la aceleración para este punto. Usando las expresiones en coordenadas polares se llega a que

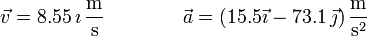
\vec{v}=8.55\,\mathrm{\imath}\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad \vec{a}=\left(15.5\vec{\imath}-73.1\,\vec{\jmath}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

Este punto corresponde al primer cuarto de periodo. En él la rapidez está aumentando, y por tanto la aceleración tangencial es positiva. La aceleración normal es no nula y va hacia adentro de la circunferencia. Ello nos da el resultado de la figura.

6 Lanzamiento horizontal desde una torre

Una partícula se lanza horizontalmente con una rapidez de 8.0 m/s desde una torre de 20.0 m de altura, estando sometida exclusivamente a la aceleración de la gravedad.

6.1 Pregunta 1

¿Cuánto tarda aproximadamente en impactar con el suelo y a qué distancia de la torre lo hace?

  • A 0.8 s y 6.4 m
  • B 2.5 s y 20 m
  • C 1.4 s y 11 m
  • D 2.0 s y 16 m
Solución

La respuesta correcta es la D.

El movimiento de una partícula sometida exclusivamente a la acción de la gravedad es un movimiento parabólico, cuya ecuación horaria es

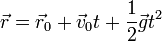
\vec{r}=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{g}t^2

donde

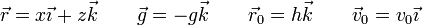
\vec{r}=x\vec{\imath}+z\vec{k}\qquad \vec{g}=-g\vec{k}\qquad\vec{r}_0 = h\vec{k}\qquad\vec{v}_0 = v_0\vec{\imath}

lo que nos da

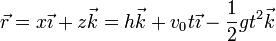
\vec{r}=x\vec{\imath}+z\vec{k} = h\vec{k}+v_0t\vec{\imath}-\frac{1}{2}gt^2\vec{k}

Separando por componentes

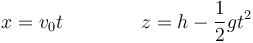
x = v_0 t\qquad\qquad z = h -\frac{1}{2}gt^2

El movimiento es una superposición de un movimiento uniforme en la dirección horizontal con uno uniformemente acelerado en la vertical.

El impacto se produce cuando la altura se hace igual a 0.

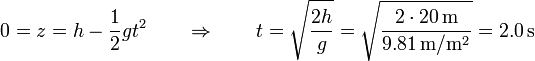
0 = z = h - \frac{1}{2}gt^2\qquad\Rightarrow\qquad t = \sqrt{\frac{2h}{g}}= \sqrt{\frac{2\cdot 20\,\mathrm{m}}{9.81\,\mathrm{m}/\mathrm{m}^2}} = 2.0\,\mathrm{s}

La distancia de la torre a la cual impacta la da el desplazamiento horizontal en el mismo tiempo

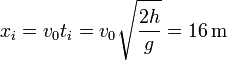
x_i = v_0 t_i = v_0\sqrt{\frac{2h}{g}}=16\,\mathrm{m}

6.2 Pregunta 2

¿Con qué rapidez impacta con el suelo?

  • A 8.0 m/s
  • B 21.4 m/s
  • C 19.8 m/s
  • D -19.8 m/s
Solución

La respuesta correcta es la B.

La velocidad con la que se mueve la partícula en cada instante es

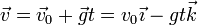
\vec{v}=\vec{v}_0+\vec{g}t = v_0\vec{\imath}-gt\vec{k}

En el momento del impacto esta velocidad vale

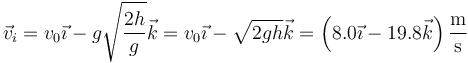
\vec{v}_i = v_0\vec{\imath}-g\sqrt{\frac{2h}{g}}\vec{k}=v_0\vec{\imath}-\sqrt{2gh}\vec{k}=\left(8.0\vec{\imath}-19.8\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}

La rapidez con la que impacta la masa es el módulo de esta velocidad

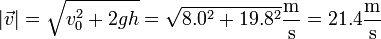
|\vec{v}|=\sqrt{v_0^2+2gh}=\sqrt{8.0^2+19.8^2}\frac{\mathrm{m}}{\mathrm{s}} = 21.4\frac{\mathrm{m}}{\mathrm{s}}

7 Estudio de magnitudes instantáneas

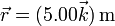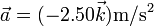En un instante dado, una partícula ocupa la posición \vec{r}=(5.00\vec{k})\,\mathrm{m}, tiene una velocidad \vec{v}=(4.00\vec{\jmath}+3.00\vec{k})\mathrm{m}/\mathrm{s} y una aceleración \vec{a}=(-2.50\vec{k})\mathrm{m}/\mathrm{s}^2.

7.1 Pregunta 1

¿Cuánto valen en dicho instante su aceleración tangencial y su aceleración normal, medidas en m/s²?

  • A at = 0.00 y an = 2.50
  • B at = 2.00 y an = 1.50
  • C at = − 2.50 y an = 0.00
  • D at = − 1.50 y an = 2.00
Solución

La respuesta correcta es la D.

No podemos hallar la aceleración tangencial como la derivada de la rapidez, ya que la conocemos en un solo instante. En su lugar, calculamos esta componente como la proyección sobre la velocidad. En forma escalar

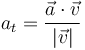
a_t = \frac{\vec{a}\cdot\vec{v}}{|\vec{v}|}

Siendo la rapidez

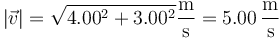
|\vec{v}| = \sqrt{4.00^2+3.00^2}\frac{\mathrm{m}}{\mathrm{s}}=5.00\,\frac{\mathrm{m}}{\mathrm{s}}

y

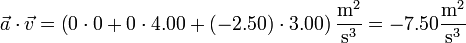
\vec{a}\cdot\vec{v}=\left(0\cdot 0+0\cdot 4.00+(-2.50)\cdot 3.00\right)\frac{\mathrm{m}^2}{\mathrm{s}^3}=-7.50\frac{\mathrm{m}^2}{\mathrm{s}^3}

Así obtenemos

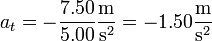
a_t = -\frac{7.50}{5.00}\frac{\mathrm{m}}{\mathrm{s}^2}=-1.50\frac{\mathrm{m}}{\mathrm{s}^2}

Con esto ya tenemos la respuesta correcta, pues hay solo una con este valor, la D.

No obstante, podemos hallar la aceleración normal escalar

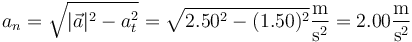
a_n = \sqrt{|\vec{a}|^2-a_t^2}=\sqrt{2.50^2-(1.50)^2}\frac{\mathrm{m}}{\mathrm{s}^2}=2.00\frac{\mathrm{m}}{\mathrm{s}^2}

7.2 Pregunta 2

¿Cuánto vale el radio de curvatura en dicho instante?

  • A R = 10.0 m
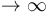
  • B R \to\infty\,
  • C R = 16.7 m
  • D R = 12.5 m
Solución

La respuesta correcta es la D.

Una vez que tenemos la rapidez y la aceleración normal calculamos el radio de curvatura

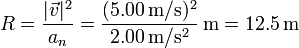
R = \frac{|\vec{v}|^2}{a_n}= \frac{(5.00\,\mathrm{m}/\mathrm{s})^2}{2.00\,\mathrm{m}/\mathrm{s}^2}\,\mathrm{m}=12.5\,\mathrm{m}

7.3 Pregunta 3

¿Cuál es su posición en m y su velocidad en m/s un tiempo Δt = 10 s más tarde?

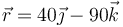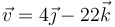  • A \vec{r}= 40\vec{\jmath}-90\vec{k} y \vec{v}=4\vec{\jmath}-22\vec{k}.
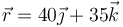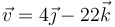  • B \vec{r}=40\vec{\jmath}+35\vec{k} y \vec{v}=4\vec{\jmath}-22\vec{k}.
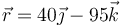  • C \vec{r}= 40\vec{\jmath}-95\vec{k} y \vec{v}=4\vec{\jmath}+3\vec{k}.
  • D No hay información suficiente para calcularlas.
Solución

La respuesta correcta es la D.

Para hallar la posición en un instante posterior no nos basta con los datos de la posición, la velocidad y la aceleración en un instante dado. No sabemos cómo cambian en el tiempo estas cantidades y por tanto no disponemos de información suficiente para responder a esta pregunta.

8 Caso de aceleración tangencial constante

Una partícula se mueve a lo largo de una circunferencia de radio R en el plano OXY con centro el origen, de forma que su aceleración tangencial es constante. En este movimiento la aceleración normal…

  • A aumenta cuadráticamente con el tiempo, an = At2 + Bt + C
  • B puede tener cualquier valor y cualquier variación
  • C es constante.
  • D aumenta linealmente con el tiempo, an = At + B
Solución

La respuesta correcta es la A.

Si la aceleración tangencial es constante, quiere decir que la rapidez varía linealmente con el tiempo

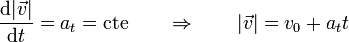
\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=a_t =\mathrm{cte}\qquad\Rightarrow\qquad |\vec{v}| = v_0+ a_t t

y por tanto la aceleración normal aumenta cuadráticamente con el tiempo

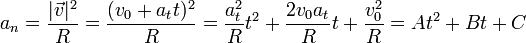
a_n = \frac{|\vec{v}|^2}{R} = \frac{(v_0+a_tt)^2}{R}=\frac{a_t^2}{R}t^2+\frac{2v_0a_t}{R}t+\frac{v_0^2}{R} = At^2+B t + C

9 Varillas que giran en sentidos opuestos

Se tiene una pequeña anilla P ensartada en la intersección de dos barras situadas en el plano XY: una pasa por el origen de coordenadas, girando uniformemente con velocidad angular Ω; la otra gira en sentido opuesto con la misma velocidad angular en valor absoluto en torno a un punto del eje OX situado a una distancia L del origen. En t = 0 ambas barras coinciden con el propio eje OX

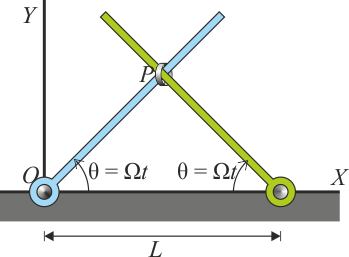
Archivo:varillas-rotatorias-simetricas.png

9.1 Pregunta 1

¿Qué trayectoria sigue la anilla?

  • A Circular
  • B Parabólica
  • C Rectilínea
  • D Helicoidal
Solución

La respuesta correcta es la C.

Las dos varillas giran con la misma velocidad angular pero en sentidos opuestos, partiendo ambas del valor 0. Esto quiere decir que en todo instante, los ángulos en O y en A son iguales y el triángulo OPA es isósceles. Por tanto, el punto P se encuentra siempre sobre el punto medio de la base y su movimiento es estrictamente vertical.

Archivo:varillas-opuestas.gif

Analíticamente podemos ver que si la partícula se encuentra en

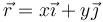
\vec{r} = x\vec{\imath}+y\vec{\jmath}

debe cumplirse

\frac{y}{x}=\mathrm{tg}(\Omega t)\qquad\qquad \frac{y}{L-x}=\mathrm{tg}(\Omega t)

y por tanto

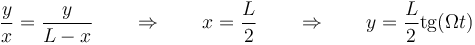
\frac{y}{x}=\frac{y}{L-x}\qquad \Rightarrow\qquad x = \frac{L}{2}\qquad\Rightarrow\qquad y = \frac{L}{2}\mathrm{tg}(\Omega t)

Vemos que efectivamente la anilla asciende por la recta x = L/2. Su ecuación horaria es

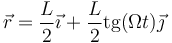
\vec{r}=\frac{L}{2}\vec{\imath}+\frac{L}{2}\mathrm{tg}(\Omega t)\vec{\jmath}

9.2 Pregunta 2

¿Cuales son las ecuaciones horarias de P en coordenadas polares?

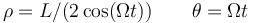
  • A \rho = L/(2\cos(\Omega t))\qquad \theta = \Omega t
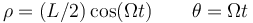
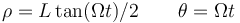
  • B \rho = (L/2)\cos(\Omega t)\qquad \theta = \Omega t
  • C \rho = L\tan(\Omega t)/2\qquad \theta = \Omega t
  • D \rho = L/2\qquad \theta = \Omega t
Solución

La respuesta correcta es la A.

Para pasar de cartesianas a polares tenemos las relaciones

x = \rho\cos(\theta)\qquad \qquad y = \rho\,\mathrm{sen}(\theta)

y sus opuestas

\rho = \sqrt{x^2+y^2}\qquad \theta=\mathrm{arctg}\left(\frac{y}{x}\right)
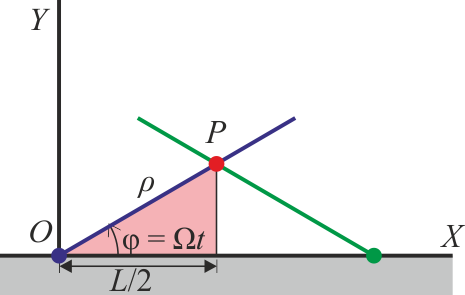
Archivo:varilla-rotatoria-triangulo.png

En este caso evidentemente el ángulo θ coincide con el ángulo θ

θ = θ = Ωt

mientras que ρ es la hipotenusa de un triángulo cuyo cateto contiguo mide L/2

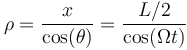
\rho = \frac{x}{\cos(\theta)} = \frac{L/2}{\cos(\Omega t)}

(o directamente a partir de la raíz cuadrada por el teorema de Pitágoras).

Las coordenadas polares de la anilla son entonces

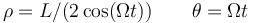
\rho = L/(2\cos(\Omega t))\qquad \theta = \Omega t

9.3 Pregunta 3

¿Cuánto vale su aceleración como función del tiempo?

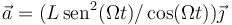
  • A \vec{a}=(L\,\mathrm{sen}^2(\Omega t)/\cos(\Omega t))\vec{\jmath}
  • B \vec{a}=(L\Omega^2\,\mathrm{sen}(\Omega t)/\cos^3(\Omega t))\vec{\jmath}
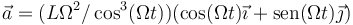
  • C \vec{a}=(L\Omega^2/\cos^3(\Omega t))(\cos(\Omega t)\vec{\imath}+\mathrm{sen}(\Omega t)\vec{\jmath})
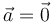
  • D \vec{a}=\vec{0}
Solución

La respuesta correcta es la B.

Podemos responder a esta pregunta sin necesidad de calcular la aceleración.

La partícula se mueve de forma no uniforme, por lo que su aceleración no es nula. Esto descarta la respuesta D.

La anilla describe un movimiento rectilíneo en todo momento, por lo que la velocidad y la aceleración llevan la dirección de la recta de movimiento, que tiene la dirección de \vec{\jmath}. Por ello la respuesta B no puede ser correcta.

Quedan las opciones A y B. La aceleración tiene dimensiones de L/T², pero la opción de la respuesta A tiene dimensiones de longitud solamente, por lo que no puede ser correcta. Por tanto, solo queda la opción B.

Veamos que efectivamente es así calculando la aceleración. Teníamos que

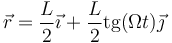
\vec{r}=\frac{L}{2}\vec{\imath}+\frac{L}{2}\mathrm{tg}(\Omega t)\vec{\jmath}

Calculamos la velocidad derivando una vez respecto al tiempo

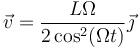
\vec{v}=\frac{L\Omega}{2\cos^2(\Omega t)}\vec{\jmath}

y derivando otra vez obtenemos la aceleración

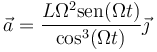
\vec{a}=\frac{L\Omega^2\mathrm{sen}(\Omega t)}{\cos^3(\Omega t)}\vec{\jmath}

10 Estudio de movimiento instantáneo

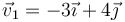En un instante dado una partícula se encuentra en \vec{r}_1=2\vec{\imath}-3\vec{k} (m), moviéndose con velocidad \vec{v}_1 = -3\vec{\imath}+4\vec{\jmath} (m/s)y aceleración 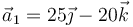\vec{a}_1 = 25\vec{\jmath}-20\vec{k} (m/s²). En ese instante…

10.1 Pregunta 1

¿cuánto vale la aceleración tangencial (escalar)?

  • A Necesitamos conocer como varía |\vec{v}| con el tiempo.
  • B 20 m/s²
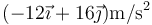
  • C (-12\vec{\imath}+16\vec{\jmath})\mathrm{m}/\mathrm{s}^2
  • D 0 m/s²
Solución

La respuesta correcta es la B.

La aceleración tangencial la calculamos proyectando la aceleración sobre la velocidad

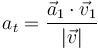
a_t=\frac{\vec{a}_1\cdot\vec{v}_1}{|\vec{v}|}

siendo la rapidez

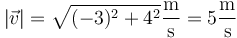
|\vec{v}|=\sqrt{(-3)^2+4^2}\frac{\mathrm{m}}{\mathrm{s}}=5\frac{\mathrm{m}}{\mathrm{s}}

Esto da

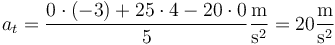
a_t = \frac{0\cdot(-3)+25\cdot 4-20\cdot 0}{5}\frac{\mathrm{m}}{\mathrm{s}^2}=20\frac{\mathrm{m}}{\mathrm{s}^2}

10.2 Pregunta 2

¿cuánto vale la aceleración normal (vector)?

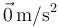
  • A \vec{0}\,\mathrm{m}/\mathrm{s}^2
  • B 25 m/s²
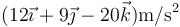
  • C (12\vec{\imath}+9\vec{\jmath}-20\vec{k})\mathrm{m}/\mathrm{s}^2
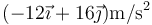
  • D (-12\vec{\imath}+16\vec{\jmath})\mathrm{m}/\mathrm{s}^2
Solución

La respuesta correcta es la C.

Podemos calcular la aceleración normal sin necesidad de hallar la tangencial calculando la componente ortogonal de la aceleración

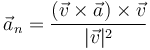
\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}

El primer producto vectorial vale

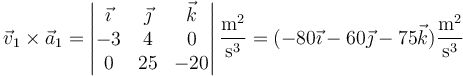
\vec{v}_1\times\vec{a}_1=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -3 & 4 & 0 \\ 0 & 25 & -20\end{matrix}\right|\frac{\mathrm{m}^2}{\mathrm{s}^3}=(-80\vec{\imath}-60\vec{\jmath}-75\vec{k})\frac{\mathrm{m}^2}{\mathrm{s}^3}

y el segundo

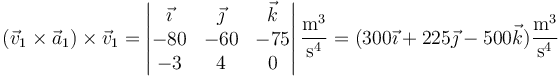
(\vec{v}_1\times\vec{a}_1)\times\vec{v}_1=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -80 & -60 & -75 \\ -3 & 4 & 0 \end{matrix}\right|\frac{\mathrm{m}^3}{\mathrm{s}^4}=(300\vec{\imath}+225\vec{\jmath}-500\vec{k})\frac{\mathrm{m}^3}{\mathrm{s}^4}

y obtenemos finalmente

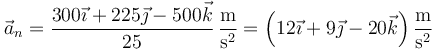
\vec{a}_n = \frac{300\vec{\imath}+225\vec{\jmath}-500\vec{k}}{25}\,\frac{\mathrm{m}}{\mathrm{s}^2}=\left(12\vec{\imath}+9\vec{\jmath}-20\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}^2}

10.3 Pregunta 3

¿cuánto vale el radio de curvatura?

  • A 1.25 m.
  • B 1 m.
  • C No hay información suficiente para hallarlo.
  • D 0.80 m.
Solución

La respuesta correcta es la A.

El radio de curvatura lo podemos calcular con la expresión

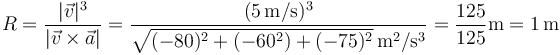
R=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}=\frac{(5\,\mathrm{m}/\mathrm{s})^3}{\sqrt{(-80)^2+(-60^2)+(-75)^2}\,\mathrm{m}^2/\mathrm{s}^3}=\frac{125}{125}\mathrm{m}=1\,\mathrm{m}

11 Movimiento circular en función del ángulo

Una partícula describe un movimiento circular de radio R en el plano XY alrededor del origen de coordenadas de forma que su velocidad angular cumple en cada instante

\vec{\omega}=\left(\sqrt{C\theta}\right)\vec{k}

siendo C una constante positiva y θ = θ(t) el ángulo que el vector de posición forma con el eje OX. La partícula parte en t = 0 desde θ = π / 2.

11.1 Pregunta 1

¿Qué tipo de movimiento describe esta partícula?

  • A Circular uniformemente acelerado.
  • B Oscilatorio a lo largo de la circunferencia.
  • C Uno con aceleración angular que va como 1/\sqrt{\theta}
  • D Circular uniforme.
Solución

La respuesta correcta es la A.

Este problema es la versión circular de uno rectilíneo.

Para identificar el movimiento calculamos su aceleración angular. Esta se define como la derivada de la velocidad angular respecto al tiempo

\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}

siendo

\vec{\omega}=\omega\vec{k}\qquad\qquad \omega = \sqrt{C\theta}

En este caso tenemos la velocidad angular como función del ángulo por lo que aplicamos la regla de la cadena

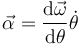
\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}\theta}\dot{\theta}

pero

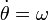
\dot{\theta}=\omega

así que la aceleración angular equivale a

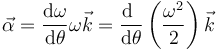
\vec{\alpha}=\frac{\mathrm{d}\omega}{\mathrm{d}\theta}\omega\vec{k}=\frac{\mathrm{d}\ }{\mathrm{d}\theta}\left(\frac{\omega^2}{2}\right)\vec{k}

Elevando al cuadrado

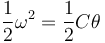
\frac{1}{2}\omega^2 = \frac{1}{2}C\theta

así que queda

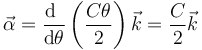
\vec{\alpha}=\frac{\mathrm{d}\ }{\mathrm{d}\theta}\left(\frac{C\theta}{2}\right)\vec{k}=\frac{C}{2}\vec{k}

La aceleración angular es constante y por tanto el movimiento es circular uniformemente acelerado.

11.2 Pregunta 2

En este movimiento, ¿son constantes las aceleraciones tangencial y normal (escalares)?

  • A La tangencial sí, pero la normal no.
  • B Las dos son constantes.
  • C No son constantes ni una ni la otra.
  • D La normal sí, pero la tangencial no.
Solución

La respuesta correcta es la A.

La aceleración tangencial (tangencial) en un movimiento circular es igual a

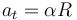
a_t=\alpha R\,

En este caso sabemos que la aceleración angular es constante, por lo que la tangencial también lo es

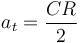
a_t = \frac{CR}{2}\,

La aceleración normal, en cambio, aumenta al crecer la velocidad angular

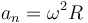
a_n =\omega^2R\,

Por tanto en este movimiento la aceleración tangencial (escalar) es constante y la normal no.

11.3 Pregunta 3

¿Cuánto vale la aceleración lineal de la partícula en t = 0?

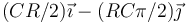
  • A (C R/2)\vec{\imath}-(RC\pi/2)\vec{\jmath}
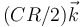
  • B (CR/2)\vec{k}
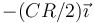
  • C -(C R/2)\vec{\imath}
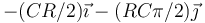
  • D -(C R/2)\vec{\imath}-(RC\pi/2)\vec{\jmath}
Solución

La respuesta correcta es la D.

En t = 0 la partícula se encuentra en θ = π / 2, esto quiere decir que su vector de posición instantáneo es

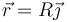
\vec{r} = R\vec{\jmath}

Para este punto la velocidad angular es

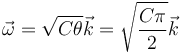
\vec{\omega}=\sqrt{C\theta}\vec{k}=\sqrt{\frac{C\pi}{2}}\vec{k}

y la aceleración angular

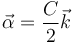
\vec{\alpha}=\frac{C}{2}\vec{k}

Con todo esto, podemos calcular la aceleración mediante la fórmula

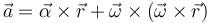
\vec{a}=\vec{\alpha}\times\vec{r}+\vec{\omega}\times(\vec{\omega}\times\vec{r})

El primer término, el vector aceleración tangencial vale

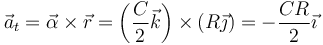
\vec{a}_t=\vec{\alpha}\times\vec{r}=\left(\frac{C}{2}\vec{k}\right)\times(R\vec{\jmath})=-\frac{CR}{2}\vec{\imath}

y el segundo, la aceleración normal

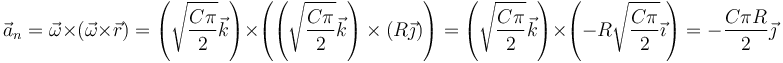
\vec{a}_n=\vec{\omega}\times(\vec{\omega}\times\vec{r})=\left(\sqrt{\frac{C\pi}{2}}\vec{k}\right)\times\left(\left(\sqrt{\frac{C\pi}{2}}\vec{k}\right)\times\left(R\vec{\jmath}\right)\right)= \left(\sqrt{\frac{C\pi}{2}}\vec{k}\right)\times\left(-R\sqrt{\frac{C\pi}{2}}\vec{\imath}\right)=-\frac{C\pi R}{2}\vec{\jmath}

12 Movimiento circular

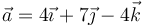Una partícula describe un movimiento circular uniforme tal que en t = 0 pasa por el origen de coordenadas con velocidad \vec{v}=2\vec{\imath}+8\vec{\jmath}+16\vec{k} (m/s) y con aceleración \vec{a}=4\vec{\imath}+7\vec{\jmath}-4\vec{k} (m/s²).

12.1 Pregunta 1

¿Cuál es la posición del centro de curvatura, \vec{r}_c?

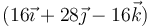  • A (16\vec{\imath}+28\vec{\jmath}-16\vec{k}) m
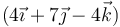  • B (4\vec{\imath}+7\vec{\jmath}-4\vec{k}) m
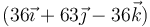  • C (36\vec{\imath}+63\vec{\jmath}-36\vec{k}) m
  • D \vec{0} m
Solución

La respuesta correcta es la A.

En este instante, la aceleración es puramente normal

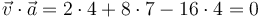
\vec{v}\cdot\vec{a}=2\cdot 4+8\cdot 7-16\cdot 4 = 0

por lo que el vector normal es el unitario en la dirección y sentido de la aceleración

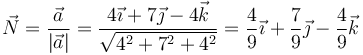
\vec{N}=\frac{\vec{a}}{|\vec{a}|}= \frac{4\vec{\imath}+7\vec{\jmath}-4\vec{k}}{\sqrt{4^2+7^2+4^2}}=\frac{4}{9}\vec{\imath}+\frac{7}{9}\vec{\jmath}-\frac{4}{9}\vec{k}

La rapidez en este instante es

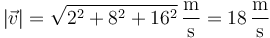
|\vec{v}|=\sqrt{2^2+8^2+16^2}\,\frac{\mathrm{m}}{\mathrm{s}}=18\,\frac{\mathrm{m}}{\mathrm{s}}

y el radio de curvatura vale

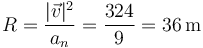
R=\frac{|\vec{v}|^2}{a_n}=\frac{324}{9}=36\,\mathrm{m}

por lo que el centro de curvatura se encuentra en

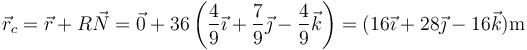
\vec{r}_c=\vec{r}+R\vec{N}=\vec{0}+36\left(\frac{4}{9}\vec{\imath}+\frac{7}{9}\vec{\jmath}-\frac{4}{9}\vec{k}\right)=(16\vec{\imath}+28\vec{\jmath}-16\vec{k})\mathrm{m}

12.2 Pregunta 2

¿Cuál es el desplazamiento de la partícula entre t = 0 s y t = 4π s?

  • A No hay información suficiente para saberlo.
  • B \vec{0} m
  • C 36 m
  • D 72π m
Solución

La respuesta correcta es la B.

La rapidez de una partícula que describe un movimiento circular uniforme es igual a

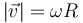
|\vec{v}|=\omega R

y el periodo de revolución

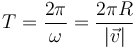
T=\frac{2\pi}{\omega}=\frac{2\pi R}{|\vec{v}|}

En este caso

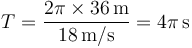
T=\frac{2\pi\times 36\,\mathrm{m}}{18\,\mathrm{m}/\mathrm{s}}=4\pi\,\mathrm{s}

Por tanto, el intervalo que se da es justamente un periodo completo, al final del cual la partícula se encuentra en el mismo punto que al principio y el desplazamiento es nulo.

13 Movimiento en polares

Una partícula se mueve en el plano de forma que en todo momento sus coordenadas polares verifican

\rho(t)=\frac{A}{t}\qquad\qquad \theta(t)=B t^2

con A y B constantes. Para esta partícula es constante…

  • A la aceleración
  • B la componente radial de la velocidad.
  • C la componente acimutal de la velocidad.
  • D la rapidez.
Solución

La respuesta correcta es la C.

La velocidad, expresada en polares, es de la forma

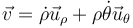
\vec{v}=\dot{\rho}\vec{u}_\rho+\rho\dot{\theta}\vec{u}_\theta

siendo en este caso

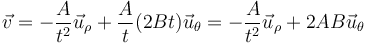
\vec{v}=-\frac{A}{t^2}\vec{u}_\rho+\frac{A}{t}(2Bt)\vec{u}_\theta= -\frac{A}{t^2}\vec{u}_\rho+2AB\vec{u}_\theta

Vemos que la componente acimutal de la velocidad es una constante, 2AB.

La rapidez y la aceleración no son constantes, como se comprueba sustituyendo en la fórmulas

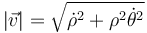
|\vec{v}|=\sqrt{\dot{\rho}^2+\rho^2\dot{\theta}^2}

y

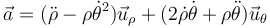
\vec{a}=(\ddot{\rho}-\rho\dot{\theta}^2)\vec{u}_\rho+(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})\vec{u}_\theta

14 Triedro de Frenet

En el movimiento de una partícula, en un instante dado el vector tangente a la trayectoria es \vec{T}=0.64\vec{\imath}-0.60\vec{\jmath}+0.48\vec{k}

14.1 Pregunta 1

¿Cuál de los siguientes vectores puede ser el vector normal, \vec{N}, de dicho movimiento?

  • A \vec{N}=-0.30\vec{\imath}+0.40\vec{k}
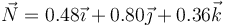
  • B \vec{N}=0.48\vec{\imath}+0.80\vec{\jmath}+0.36\vec{k}
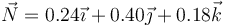
  • C \vec{N}=0.24\vec{\imath}+0.40\vec{\jmath}+0.18\vec{k}
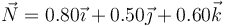
  • D \vec{N}=0.80\vec{\imath}+0.50\vec{\jmath}+0.60\vec{k}
Solución

La respuesta correcta es la B.

El vector normal debe ser unitario y ortogonal a \vec{T}. El único unitario es el de la opción B.

14.2 Pregunta 2

Y dados los vectores \vec{T} y \vec{N} anteriores, ¿cuál puede ser el vector binormal, \vec{B}?

  • A \vec{B}=-0.80\vec{\imath}+0.60\vec{k}
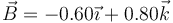
  • B \vec{B}=-0.60\vec{\imath}+0.80\vec{k}
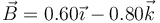
  • C \vec{B}=0.60\vec{\imath}-0.80\vec{k}
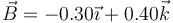
  • D \vec{B}=-0.30\vec{\imath}+0.40\vec{k}
Solución

La respuesta correcta es la B.

Se calcula como

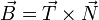
\vec{B}=\vec{T}\times\vec{N}

lo que da

\vec{B}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0.64 & -0.60 & 0.48 \\ 0.48 & 0.80 & 0.36 \end{matrix}\right|=\left\{\begin{array}{rc}\left(-0.60\times 0.36-0.48\times 0.80\right)\vec{\imath} & + \\ \left(0.48\times 0.48-0.64\times 0.36\right)\vec{\jmath}& + \\ \left(0.64\times 0.80+0.60\times 0.48\right)\vec{k}&\end{array}\right\}=-0.60\vec{\imath}+0\vec{\jmath}+0.80\vec{k}

Obtenido de "http://tesla.us.es/wiki/index.php/Preguntas_de_test_de_cinem%C3%A1tica_tridimensional_de_la_part%C3%ADcula_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace