Entrar Página Discusión Historial Go to the site toolbox

Diadas y productos diádicos

De Laplace

(Diferencias entre revisiones)
Línea 45: Línea 45:
===Traza===
===Traza===
La traza del producto diádico se define como la suma de los elementos diagonales. Se deduce entonces que
La traza del producto diádico se define como la suma de los elementos diagonales. Se deduce entonces que
-
<center></math>
+
<center><math>
\mathrm{Tr}(\vec{A}\vec{B})=A_xB_x+A_yB_y+A_zB_z=\vec{A}\cdot\vec{B}
\mathrm{Tr}(\vec{A}\vec{B})=A_xB_x+A_yB_y+A_zB_z=\vec{A}\cdot\vec{B}
</math></center>
</math></center>
Línea 67: Línea 67:
También se puede multiplicar simultaneamente por ambos lados. En este caso, el resultado es un número.
También se puede multiplicar simultaneamente por ambos lados. En este caso, el resultado es un número.
<center><math>
<center><math>
-
\vec{C}\cdot(\vec{A}\vec{B})\cdot\bD=(\vec{C}\cdot\vec{A})(\vec{B}\cdot\bD)
+
\vec{C}\cdot(\vec{A}\vec{B})\cdot\vec{D}=(\vec{C}\cdot\vec{A})(\vec{B}\cdot\vec{D})
</math></center>
</math></center>
Asimismo se puede multiplicar vectorialmente
Asimismo se puede multiplicar vectorialmente
Línea 78: Línea 78:
De la propiedad de linealidad resulta de forma inmediata que
De la propiedad de linealidad resulta de forma inmediata que
<center><math>
<center><math>
-
\vec{A}\vec{B}=\left(\sum_iA_i\bu{i}\right)\left(\sum_jB_j\bu{j}\right)=
+
\vec{A}\vec{B}=\left(\sum_iA_i\vec{u}_i\right)\left(\sum_kB_j\vec{u}_j\right)=
-
\sum_{i,j}A_iB_j\bu{i}\bu{j}
+
\sum_{i,j}A_iB_j\vec{u}_i\vec{u}_j
</math></center>
</math></center>
por lo que, conocidos los productos diádicos de los vectores de la base, podemos expresar cualquier diada en función de ellos. Por su parte, se tiene que, por ejemplo,
por lo que, conocidos los productos diádicos de los vectores de la base, podemos expresar cualquier diada en función de ellos. Por su parte, se tiene que, por ejemplo,
Línea 85: Línea 85:
\vec{\imath}\vec{\jmath}=\left(\begin{matrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right)
\vec{\imath}\vec{\jmath}=\left(\begin{matrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right)
</math></center>
</math></center>
-
En general, el producto de dos vectores unitarios en cartesianas puede  
+
En general, el producto de dos vectores unitarios en cartesianas puede representarse, en forma matricial, como una matriz con un elemento unitario y los demás nulos. Por ello, podemos concluir que los productos diádicos de los vectores unitarios forman un sistema generador del conjunto de las diadas.  
-
representarse, en forma matricial, como una matriz con un elemento unitario  
+
==Tensores cartesianos==
-
y los demás nulos. Por ello, podemos concluir que los productos diádicos de  
+
Partiendo de la analogía tensor/matriz puede extenderse lo dicho a todos los tensores, esto es,  
-
los vectores unitarios forman un sistema generador del conjunto de las  
+
''cualquier tensor puede expresarse como combinación lineal de diadas unitarias''. En forma algebraica
-
diadas.  
+
-
==Tensores cartesianos}
+
-
Partiendo de la analogía tensor/matriz puede extenderse lo dicho a  
+
-
todos los tensores, esto es,  
+
-
''cualquier tensor puede expresarse como combinación lineal de diadas  
+
-
unitarias}. En forma algebraica
+
<center><math>
<center><math>
-
\mathcal{M}=\sum_{ij}M_{ij}\bu{i}\bu{j}
+
\mathcal{M}=\sum_{ij}M_{ij}\vec{u}_i\vec{u}_j
</math></center>
</math></center>
donde los <math>M_{ij}</math> son los elementos de la matriz que representa al tensor  
donde los <math>M_{ij}</math> son los elementos de la matriz que representa al tensor  
Línea 104: Línea 98:
expresarse asimismo en su forma diádica.
expresarse asimismo en su forma diádica.
-
===Tensor unidad (o identidad)}
+
===Tensor unidad (o identidad)===
-
Un tensor especialmente importante es el unitario, que se caracteriza por  
+
Un tensor especialmente importante es el unitario, que se caracteriza por que todos los elementos de la diagonal valen la unidad y el resto son nulos.  
-
que todos los elementos de la diagonal valen la unidad y el resto son nulos.  
+
Se sigue que
Se sigue que
<center><math>
<center><math>
Línea 118: Línea 111:
=\vec{\imath}A_x+\vec{\jmath}A_y+\vec{k}A_z=\vec{A}
=\vec{\imath}A_x+\vec{\jmath}A_y+\vec{k}A_z=\vec{A}
</math></center>
</math></center>
-
==Cambios de base}
+
==Cambios de base==
-
Con lo dicho hasta ahora no se evidencia ninguna ventaja de la  
+
Con lo dicho hasta ahora no se evidencia ninguna ventaja de la expresión diádica de un tensor sobre la expresión matricial. Estas aparecen cuando se considera que mientras que la última es válida sólo en coordenadas cartesianas, la primera es manejable tanto en su forma abstracta como en cualquier sistema.
-
expresión diádica de un tensor sobre la expresión matricial. stas
+
-
aparecen cuando se considera que mientras que la última es válida sólo en  
+
-
coordenadas cartesianas, la primera es manejable tanto en su forma  
+
-
abstracta como en cualquier sistema.
+
Consideremos, por ejemplo, la diada
Consideremos, por ejemplo, la diada
<center><math>
<center><math>
-
\mathcal{M}=\br\vec{r}=x^2\vec{\imath}\vec{\imath}+xy(\vec{\imath}\vec{\jmath}+\vec{\jmath}\vec{\imath})+\cdots+
+
\mathcal{M}=\vec{r}\vec{r}=x^2\vec{\imath}\vec{\imath}+xy(\vec{\imath}\vec{\jmath}+\vec{\jmath}\vec{\imath})+\cdots+
z^2\vec{k}\vec{k}
z^2\vec{k}\vec{k}
</math></center>
</math></center>
-
Tanto esta expresión como la matricial tienen nueve componentes no nulas.  
+
Tanto esta expresión como la matricial tienen nueve componentes no nulas. Sin embargo, si empleamos coordenadas esféricas queda
-
Sin embargo, si empleamos coordenadas esféricas queda
+
<center><math>
<center><math>
-
\mathcal{M}=\br\vec{r}=r^2\bu{r}\bu{r}
+
\mathcal{M}=\vec{r}\vec{r}=r^2\vec{u}_r\vec{u}_r
</math></center>
</math></center>
-
esto es, sólo una componente es no nula y, por tratarse del mismo tensor  
+
esto es, sólo una componente es no nula y, por tratarse del mismo tensor (que, recordemos, es independiente del sistema de coordenadas) es mucho más fácil trabajar con esta expresión.
-
(que, recordemos, es independiente del sistema de coordenadas) es mucho más  
+
-
fácil trabajar con esta expresión.
+
-
Hay que remarcar que, cuando se usan coordenadas no cartesianas, la  
+
Hay que remarcar que, cuando se usan coordenadas no cartesianas, la expresión matricial del tensor carece de utilidad (en cuanto que no se va a comportar como lo hacen las matrices &ldquo;normales&rdquo;).
-
expresión matricial del tensor carece de utilidad (en cuanto que no se va a  
+
-
comportar como lo hacen las matrices ``normales'').
+
-
En particular la expresión del tensor identidad en cualquier base ortogonal  
+
En particular la expresión del tensor identidad en cualquier base ortogonal es
-
es
+
<center><math>
<center><math>
-
\mathcal{I}=\bu{1}\bu{1}+\bu{2}\bu{2}+\bu{3}\bu{3}
+
\mathcal{I}=\vec{u}_{1}\vec{u}_{1}+\vec{u}_{2}\vec{u}_{2}+\vec{u}_{3}\vec{u}_{3}
</math></center>
</math></center>
-
Para realizar el cambio de un sistema de coordenadas a otro las reglas de  
+
Para realizar el cambio de un sistema de coordenadas a otro las reglas de transformación son análogas a las que se aplican entre vectores, sólo hay que aplicarlas a cada uno de los vectores unitarios que componen las diadas. Por ejemplo
-
transformación son análogas a las que se aplican entre vectores, sólo hay  
+
-
que aplicarlas a cada uno de los vectores unitarios que componen las diadas.  
+
-
Por ejemplo
+
<center><math>
<center><math>
-
\bu{r}\bu{r}=(\sa\bu{\rho}+\ca\vec{k})(\sa\bu{\rho}+\ca\vec{k})=</math></center><center><math>=
+
\vec{u}_r\vec{u}_r=(\mathrm{sen}(\theta)\vec{u}_{\rho}+\cos(\theta)\vec{k})(\mathrm{sen}(\theta)\vec{u}_{\rho}+\cos(\theta)\vec{k})=</math></center><center><math>=
-
\sen^2\theta\bu{\rho}\bu{\rho}+\sa\ca(\bu{\rho}\vec{k}+\vec{k}\bu{\rho})+
+
\sen^2\theta\vec{u}_{\rho}\vec{u}_{\rho}+\mathrm{sen}(\theta)\cos(\theta)(\vec{u}_{\rho}\vec{k}+\vec{k}\vec{u}_{\rho})+\cos^2\theta\vec{k}\vec{k}
-
\cos^2\theta\vec{k}\vec{k}
+
</math></center>
</math></center>
-
Es posible también construir una base del espacio de los tensores combinando  
+
Es posible también construir una base del espacio de los tensores combinando dos bases vectoriales diferentes (por ejemplo, construyendo los productos <math>\vec{\imath}\vec{u}_r</math>, <math>\vec{\jmath}\vec{u}_{\theta}</math> y similares), pero no suele ser de mucha utilidad.
-
dos bases vectoriales diferentes (por ejemplo, construyendo los productos
+
-
<math>\vec{\imath}\bu{r}</math>, <math>\vec{\jmath}\bu{\theta}</math> y similares), pero no suele ser de mucha
+
-
utilidad.
+
-
==Cálculo diferencial con diadas}
 
-
A semejanza de lo que ocurre en el caso escalar y vectorial, es posible
 
-
desarrollar el cálculo del operador nabla para diadas.
 
-
===Gradiente de un vector}
 
-
Del mismo modo que el producto escalar y vectorial de nabla por un vector
 
-
generaban la divergencia y el rotacional, respectivamente, el producto
 
-
diádico produce un tensor, conocido como el ''gradiente del vector}. En
 
-
coordenadas cartesianas, la expresión de éste es
 
-
<center><math>
 
-
(\nabla\vec{A})=\left(\begin{matrix}
 
-
\dpar{A_x}{x} & \dpar{A_y}{x} & \dpar{A_z}{x} \\
 
-
& & \\
 
-
\dpar{A_x}{y} & \dpar{A_y}{y} & \dpar{A_z}{y} \\
 
-
& & \\
 
-
\dpar{A_x}{z} & \dpar{A_y}{z} & \dpar{A_z}{z}}
 
-
</math></center>
 
-
Si se emplean coordenadas diferentes de las cartesianas es importante tener
+
==Diadas aplicadas a la física==
-
en cuenta las derivadas de los vectores unitarios.
+
La introducción de las diadas no pasaría de se un simple juego matemático si  no sirvieran para simplificar las leyes físicas. En la física aparecen frecuentemente tensores cartesianos, todos los cuales admiten la expresión diádica correspondiente. En algunos caso ésta es más simple que las expresiones matriciales correspondientes. Veamos tres ejemplos, dos de mecánica y uno de electromagnetismo.
-
 
+
-
Si el vector <math>\vec{A}</math> es el de posición <math>\br</math> resulta
+
-
<center><math>
+
-
\nabla\vec{r}=\left(\vec{\imath}\dpar{}{x}+\vec{\jmath}\dpar{}{y}+\vec{k}\dpar{}{z}\right)
+
-
(x\vec{\imath}+y\vec{\jmath}+z\vec{k})=</math></center><center><math>=
+
-
\vec{\imath}\vec{\imath}+\vec{\jmath}\vec{\jmath}+\vec{k}\vec{k}=\mathcal{I}
+
-
</math></center>
+
-
esto es, el gradiente del vector de posición es el tensor identidad. Resulta
+
-
entonces la siguiente relación
+
-
<center><math>
+
-
(\vec{A}\cdot\nabla)\br=\vec{A}\cdot(\nabla\vec{r})=\vec{A}\cdot\mathcal{I}=\vec{A}
+
-
</math></center>
+
-
 
+
-
===Divergencia de un tensor}
+
-
La divergencia de un tensor se define como el producto escalar del operador
+
-
nabla por el tensor en cuestión. Resulta entonces que son posibles
+
-
''dos} divergencias, según que el producto se haga por la derecha o por
+
-
la izquierda.
+
-
 
+
-
La divergencia de una diada es
+
-
<center><math>
+
-
\nabla\cdot(\vec{A}\vec{B})=\nabla\cdot(\underline{\vec{A}}\vec{B})+\nabla\cdot(\vec{A}\underline{\vec{B}})=
+
-
(\nabla\cdot\vec{A})\vec{B}+(\vec{A}\cdot\nabla)\vec{B}
+
-
</math></center>
+
-
 
+
-
===Otros operadores diferenciales}
+
-
Igualmente se pueden definir el rotacional de un tensor y de una diada (por
+
-
la derecha o por la izquierda)
+
-
<center><math>
+
-
\nabla\times(\vec{A}\vec{B})
+
-
</math></center>
+
-
o el gradiente del gradiente de un escalar
+
-
<center><math>
+
-
\nabla\nabla\phi
+
-
</math></center>
+
-
que es un tensor; el gradiente de un rotacional de un vector, etc.
+
-
 
+
-
==Teoremas integrales}
+
-
Los teoremas de Stokes y de Gauss pueden generalizarse a tensores por simple
+
-
sustitución. Así, para el de Gauss se tiene
+
-
<center><math>
+
-
\int_\tau\nabla\cdot\mathcal{T}\,d\tau
+
-
=\oint_{\partial\tau}\bn\cdot\mathcal{T}\,dS
+
-
</math></center>
+
-
(nótese que el orden de los factores es importante).
+
-
 
+
-
Igualmente puede definirse el gradiente de un vector a partir de la expresión
+
-
<center><math>
+
-
\nabla\vec{A}=\lim_{\tau\to 0}\frac{1}{\tau}\oint_{\partial\tau}\bn\vec{A}\,dS
+
-
</math></center>
+
-
y obtener el teorema integral correspondiente
+
-
<center><math>
+
-
\int_\tau \nabla\vec{A}\,d\tau=\oint_{\partial\tau} \bn\vec{A}\,dS
+
-
</math></center>
+
-
==Diadas aplicadas a la física}
+
===Matrices de rotación===
-
La introducción de las diadas no pasaría de se un simple juego matemático si
+
-
no sirvieran para simplificar las leyes físicas. En la física aparecen
+
-
frecuentemente tensores cartesianos, todos los cuales admiten la expresión
+
-
diádica correspondiente. En algunos caso ésta es más simple que las
+
-
expresiones matriciales correspondientes. Veamos tres ejemplos, uno de
+
-
mecánica y dos de electromagnetismo.
+
-
===Tensor de inercia}
+
===Tensor de inercia===
-
Cuando se estudia el sólido rígido, se introduce el tensor de inercia  
+
Cuando se estudia el sólido rígido, se introduce el tensor de inercia <math>\mathcal{J}</math> que, para un punto material, es una matriz con componentes
-
<math>\mathcal{J}</math> que, para un punto material, es una matriz con componentes
+
<center><math>
<center><math>
(\mathcal{J})=m\left(\begin{matrix}y^2+z^2 & -xy & -xz \\
(\mathcal{J})=m\left(\begin{matrix}y^2+z^2 & -xy & -xz \\
-xy & x^2+y^2 & -yz \\
-xy & x^2+y^2 & -yz \\
-
-xy & -yz & x^2+y^2}
+
-xy & -yz & x^2+y^2\end{matrix}\right)
</math></center>
</math></center>
En forma diádica este tensor se escribe simplemente como
En forma diádica este tensor se escribe simplemente como
<center><math>
<center><math>
-
\mathcal{J}=m(r^2\mathcal{I}-\br\vec{r})
+
\mathcal{J}=m(r^2\mathcal{I}-\vec{r}\vec{r})
</math></center>
</math></center>
-
Usando la expresión diádica podemos obtener, por ejemplo, el valor del  
+
Usando la expresión diádica podemos obtener, por ejemplo, el valor del momento angular
-
momento angular
+
<center><math>
<center><math>
-
\mathbf{L}=\mathcal{J}\cdot\frec=m(r^2\mathcal{I}\cdot\frec-(\br\vec{r})\cdot\frec)=</math></center><center><math>
+
\vec{L}=\mathcal{J}\cdot\vec{\omega}=m(r^2\mathcal{I}\cdot\vec{\omega}-(\vec{r}\vec{r})\cdot\vec{\omega})=</math></center><center><math>
-
m(r^2\frec-\br(\br\cdot\frec))=m\vec{r}\times(\frec\times\vec{r})
+
m(r^2\vec{\omega}-\vec{r}(\vec{r}\cdot\vec{\omega}))=m\vec{r}\times(\vec{\omega}\times\vec{r})
</math></center>
</math></center>
-
Si lo que queremos es hallar el tensor de inercia de una distribución  
+
Si lo que queremos es hallar el tensor de inercia de una distribución tendremos que
-
tendremos que
+
<center><math>
<center><math>
-
\mathcal{J}=\int \rho (r^2\mathcal{I}-\br\vec{r})\,d\tau
+
\mathcal{J}=\int \rho (r^2\mathcal{I}-\vec{r}\vec{r})\,d\tau
</math></center>
</math></center>
-
También podemos obtener el tensor de inercia para una partícula en  
+
También podemos obtener el tensor de inercia para una partícula en coordenadas esféricas como
-
coordenadas esféricas como
+
<center><math>
<center><math>
-
\mathcal{J}=m(r^2(\bu{r}\bu{r}+\bu{\theta}\bu{\theta}+\bu{\vp}\bu{\vp})-
+
\mathcal{J}=m(r^2(\vec{u}_r\vec{u}_r+\vec{u}_{\theta}\vec{u}_{\theta}+\vec{u}_{\vp}\vec{u}_{\vp})-
-
(r^2\bu{r}\bu{r}))=</math></center><center><math>=
+
(r^2\vec{u}_r\vec{u}_r))=</math></center><center><math>=
-
mr^2(\bu{\theta}\bu{\theta}+\bu{\vp}\bu{\vp})
+
mr^2(\vec{u}_{\theta}\vec{u}_{\theta}+\vec{u}_{\vp}\vec{u}_{\vp})
</math></center>
</math></center>
-
===Momento cuadrupolar}
+
===Tensor de tensiones===
-
Cuando se hace el desarrollo multipolar para calcular el potencial eléctrico
+
-
creado por una distribución de carga en puntos alejados de la misma se
+
-
obtiene que
+
-
<center><math>
+
-
\phi=\kd\left(\frac{q}{r}+\frac{\bp\cdot\vec{r}}{r^3}+
+
-
\frac{\br\cdot\mathcal{Q}\cdot\vec{r}}{r^5}+\cdots\right)
+
-
</math></center>
+
-
Los distintos coeficientes son los llamados momentos multipolares. el
+
-
primero, la carga, es un escalar. El segundo, el momento dipolar, es un
+
-
vector. El tercero, el momento cuadrupolar, es un tensor. Para una carga
+
-
puntual la expresión de este tensor es una matriz de componentes
+
-
<center><math>
+
-
Q_{ij}=q\frac{3x_ix_j-r^2\delta_{ij}}{2}
+
-
</math></center>
+
-
y expresiones integrales análogas para una distribución. En forma diádica,
+
-
el momento cuadrupolar se escribe
+
-
<center><math>
+
-
\mathcal{Q}=q\frac{3\vec{r}\br-r^2\mathcal{I}}{2}
+
-
</math></center>
+
-
Si tenemos, por ejemplo, una carga puntual situada en <math>a\vec{k}</math> tendremos
+
==&hellip;y más allá==
-
que su momento cuadrupolar respecto al origen es
+
Hasta aquí hemos hablado de las diadas como un producto entre dos vectores y lo hemos aplicado al estudio de los tensores cartesianos de segundo orden exclusivamente. Sin embargo, todo lo dicho no es más que un caso particular de un producto tensorial, extensible a cualquier orden y cualquier métrica.  
-
<center><math>
+
No existe problema en definir el producto diádico de tres vectores <math>\vec{A}\vec{B}\vec{C}</math> que sería un tensor de tercer orden, imposible de representar por una matriz.  
-
\mathcal{Q}=qa^2\frac{3\vec{k}\vec{k}-\vec{\imath}\vec{\imath}-\vec{\jmath}\vec{\jmath}-\vec{k}\vec{k}}{2}=</math></center>
+
También es posible tratar las diadas como un caso particular de aplicación lineal sobre los vectores. Cabe entonces hablar de diadas duales, de coordenadas covariantes y contravariantes, etc. Para todo ello existe bibliografía disponible.
-
<center><math>
+
-
=qa^2\frac{-\vec{\imath}\vec{\imath}-\vec{\jmath}\vec{\jmath}+2\vec{k}\vec{k}}{2}
+
-
</math></center>
+
-
los que nos da, directamente, las nueve componentes de la matriz
+
-
correspondiente
+
-
<center><math>
+
-
(\mathcal{Q})=\frac{qa^2}{2}\left(\begin{matrix}-1 & 0 & 0 \\ 0 & -1 & 0 \\
+
-
0 & 0 & 2}
+
-
</math></center>
+
-
 
+
-
Si ahora pretendemos calcular la contribución cuadrupolar al potencial
+
-
resultará
+
-
<center><math>
+
-
\phi_c=\frac{qa^2}{8\pi\eps
+
-
r^5}
+
-
\left(\br\cdot(-\vec{\imath}\vec{\imath}-\vec{\jmath}\vec{\jmath}+2\vec{k}\vec{k})\cdot\vec{r}\right)=
+
-
\frac{qa^2(2z^2-x^2-y^2)}{8\pi\eps
+
-
r^5}
+
-
</math></center>
+
-
 
+
-
===Tensor de tensiones de Maxwell}
+
-
En situaciones electrostáticas, es posible calcular la fuerza sobre un
+
-
sistema directamente a partir del campo (sin conocer la densidad de carga
+
-
que sufre la fuerza). Esto se consigue mediante el ''tensor de tensiones
+
-
de Maxwell}, en la forma
+
-
<center><math>
+
-
\bF=\oint \mathcal{T}\cdot\bn\,dS
+
-
</math></center>
+
-
esto es, la fuerza equivale al flujo sobre una superficie cerrada, que
+
-
envuelva al sistema en cuestión, del citado tensor, cuya expresión diádica es
+
-
<center><math>
+
-
\mathcal{T}=\eps\left(\bE\bE-\frac{1}{2}E^2\mathcal{I}\right)
+
-
</math></center>
+
-
Esta expresión es válida en el vacío. En un dieléctrico lineal esta
+
-
expresión se convierte en
+
-
<center><math>
+
-
\mathcal{T}=\left(\bE\bD-\frac{1}{2}\bE\cdot\bD\mathcal{I}\right)
+
-
</math></center>
+
-
La expresión matricial correspondiente, mucho más complicada, es
+
-
<center><math>
+
-
(\mathcal{T})=\frac{\eps}{2}\left(\begin{matrix}E_x^2-E_y^2-E_z^2 & 2E_xE_y & 2E_xE_z
+
-
\\
+
-
2E_xE_y & E_y^2-E_x^2-E_z^2 & 2E_yE_z
+
-
\\
+
-
2E_xE_z & 2E_yE_z & E_z^2-E_z^2-E_y^2}
+
-
</math></center>
+
-
Si además de campos eléctricos tenemos campos magnéticos presentes la
+
-
expresión del tensor de tensiones de Maxwell para el vacío es
+
-
<center><math>
+
-
\mathcal{T}=\eps\left(\bE\bE-\frac{1}{2}E^2\mathcal{I}\right)+
+
-
\frac{1}{\mu_0}\left(\vec{B}\vec{B}-\frac{1}{2}B^2\mathcal{I}\right)
+
-
</math></center>
+
-
 
+
-
==\ldots y más allá}
+
-
Hasta aquí hemos hablado de las diadas como un producto entre dos vectores y  
+
-
lo hemos aplicado al estudio de los tensores cartesianos de segundo orden  
+
-
exclusivamente. Sin embargo, todo lo dicho no es más que un caso particular  
+
-
de un producto tensorial, extensible a cualquier orden y cualquier métrica.  
+
-
No existe problema en definir el producto diádico de tres vectores  
+
-
<math>\vec{A}\vec{B}\vec{C}</math> que sería un tensor de tercer orden, imposible de representar  
+
-
por una matriz.  
+
-
También es posible tratar las diadas como un caso particular de aplicación  
+
-
lineal sobre los vectores. Cabe entonces hablar de diadas duales, de  
+
-
coordenadas covariantes y contravariantes, etc. Para todo ello existe  
+
-
bibliografía disponible.
+
-
 
+
-
==Problemas}
+
-
\renewcommand{\theenumi}{\textbf{\arabic{enumi}}}
+
-
\begin{enumerate}
+
-
\item Hallar la expresión matricial de los siguientes productos diádicos.
+
-
\begin{enumerate}
+
-
\item
+
-
<center><math>
+
-
\vec{A}\vec{B} \qquad \mathrm{con}\qquad \vec{A}=\vec{\imath}+\vec{\jmath}-2\vec{k}\qquad
+
-
\vec{B}=\vec{\imath}-\vec{k}
+
-
</math></center>
+
-
\item
+
-
<center><math>
+
-
\bu{r}\bu{r}
+
-
</math></center>
+
-
\item
+
-
<center><math>
+
-
\bu{\theta}\vec{k}
+
-
</math></center>
+
-
\end{enumerate}
+
-
\item Es fácil ver que el conjunto de las diadas no forma un espacio
+
-
vectorial, ya que la suma de dos diadas, <math>\vec{A}\vec{B}+\vec{C}\bD</math>, no será, en
+
-
general, otra diada. ¨Cuál es la condición o condiciones para que sí
+
-
se de esta relación?
+
-
\item ¨Cuáles son los autovalores de una diada, considerada como
+
-
operador que actúa en el espacio de los vectores? ¨Y los
+
-
autovectores correspondientes? En otras palabras, dada la relación
+
-
<center><math>
+
-
(\vec{A}\vec{B})\cdot\mathbf{x}=\lambda\mathbf{x}
+
-
</math></center>
+
-
hallar los valores posibles de <math>\lambda</math> y <math>\mathbf{x}</math>.
+
-
\item Repetir el problema anterior para el cálculo de los llamados
+
-
''autovectores por la izquierda}, definidos como los
+
-
<math>\mathbf{x}</math> tales que
+
-
<center><math>
+
-
\mathbf{x}\cdot(\vec{A}\vec{B})=\lambda\mathbf{x}
+
-
</math></center>
+
-
\item Se define la diada ''traspuesta} de una dada como
+
-
<center><math>
+
-
(\vec{A}\vec{B})^\mathrm{t}=\vec{B}\vec{A}
+
-
</math></center>
+
-
\begin{enumerate}
+
-
\item Demostrar que toda diada puede ponerse como suma de un tensor
+
-
simétrico (igual a su traspuesto) y de uno antisimétrico (igual a su
+
-
traspuesto cambiado de signo)
+
-
<center><math>
+
-
\vec{A}\vec{B}=\mathcal{S}+\mathcal{A}
+
-
</math></center>
+
-
Hallar <math>\mathcal{S}</math> y <math>\mathcal{A}</math> (sugerencia: hallar la
+
-
traspuesta de la expresión anterior).
+
-
\item En el cálculo anterior, ¨qué representan las componentes del
+
-
tensor antisimétrico <math>\mathcal{A}</math>?
+
-
\item ¨Cuál es la condición para que una diada sea simétrica
+
-
(<math>\vec{A}\vec{B}=\vec{B}\vec{A}</math>)? ¨Y para que sea antisimétrica (<math>\vec{A}\vec{B}=-\vec{B}\vec{A}</math>)?
+
-
\item A partir de la base cartesiana de las diadas, hallar una base
+
-
del subespacio de tensores simétricos y del de tensores
+
-
antisimétricos.
+
-
\end{enumerate}
+
-
\item Demostrar que todo tensor se puede escribir como
+
-
<center><math>
+
-
\mathcal{M}=\vec{A}\vec{\imath}+\vec{B}\vec{\jmath}+\vec{C}\vec{k}
+
-
</math></center>
+
-
¨Cuánto valen <math>\vec{A}</math>, <math>\vec{B}</math> y <math>\vec{C}</math>? Esto permite considerar los
+
-
tensores como vectores de vectores y muestra que todo tensor puede
+
-
ponerse como combinación de sólo tres diadas.
+
-
\item Expresar el tensor <math>\br\vec{r}-r^2\mathcal{I}</math> en coordenadas
+
-
cilíndricas.
+
-
\item Hallar las componentes cartesianas del tensor
+
-
<math>\mathcal{I}\times\vec{A}</math>.
+
-
\item Obtener las componentes del gradiente de un vector en
+
-
coordenadas cilíndricas. Recuérdese que
+
-
<center><math>
+
-
\dpar{\bu{\rho}}{\vp}=\bu{\vp}\qquad \dpar{\bu{\vp}}{\vp}=-\bu{\rho}
+
-
</math></center>
+
-
y todas las demas derivadas son nulas.
+
-
\item Hallar la divergencia y el rotacional del tensor <math>\vec{A}\br</math>, con
+
-
<math>\vec{A}</math> un vector constante.
+
-
\item Hallar el gradiente del campo vectorial <math>\vec{A}=r^n\bu{r}</math> y del
+
-
<math>\vec{B}=\rho^n\bu{\rho}</math>.
+
-
\item Demostrar que si un tensor es el gradiente de un vector, su
+
-
rotacional es nulo.
+
-
\item Hallar el tensor de inercia de una varilla homogénea de
+
-
longitud <math>L</math>, colocada a lo largo del eje <math>z</math> y con centro en el
+
-
origen de coordenadas.
+
-
\item Hallar el momento cuadrupolar de un anillo de radio <math>R</math> con
+
-
densidad de carga <math>\lambda</math> situado en el plano <math>xy</math> con centro el
+
-
origen de coordenadas.
+
-
\item Determinar, empleando el tensor de tensiones de Maxwell, que
+
-
una carga puntual no ejerce fuerza sobre sí misma.
+
-
\end{enumerate}
+
-
\end{document}
+

Revisión de 15:07 13 abr 2018

Contenido

1 Introducción

Lo que sigue es una introducción, bastante poco rigurosa, del concepto de producto diádico y sus posibles aplicaciones al cálculo tensorial. Al final figuran una serie de problemas de aplicación de esta técnica.

2 Definición de producto diádico

En el espacio tridimensional ordinario se suelen emplear dos productos entre vectores, el escalar, 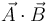\vec{A}\cdot\vec{B}, y el vectorial, 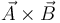\vec{A}\times\vec{B}. Como su propio nombre indica, el primero es un escalar (esto es, un número), mientras que el segundo es un vector (rigurosamente hablando, es un seudovector).

Es posible definir un tercer producto que tiene carácter tensorial. Este producto diádico (o tensorial) puede representarse en coordenadas cartesianas por una matriz 3×3 cuyos elementos son los productos de las respectivas componentes

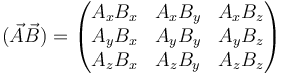
(\vec{A}\vec{B})=\left(\begin{matrix}A_xB_x &A_xB_y &A_xB_z \\ A_yB_x &A_yB_y &A_yB_z \\ A_zB_x &A_zB_y & A_zB_z\end{matrix}\right)

El producto diádico se indica sin punto, 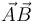\vec{A}\vec{B}. También se representa con el símbolo de producto tensorial como 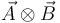\vec{A}\otimes\vec{B}. Al ente que forma se denomina diada.

Esta matriz puede obtenerse a partir de la representación de cada vector como una matriz fila o columna, ya que

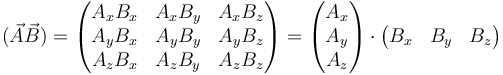
(\vec{A}\vec{B})=\left(\begin{matrix}A_xB_x &A_xB_y &A_xB_z \\ A_yB_x &A_yB_y &A_yB_z \\ A_zB_x &A_zB_y & A_zB_z\end{matrix}\right)=\left(\begin{matrix}A_x\\ A_y\\ A_z\end{matrix}\right)\cdot\left(\begin{matrix}B_x &B_y & B_z\end{matrix}\right)

Puede compararse con el producto escalar, que es

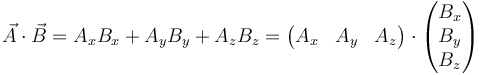
\vec{A}\cdot\vec{B}=A_xB_x+A_yB_y+A_zB_z=\left(\begin{matrix}A_x & A_y &A_z\end{matrix}\right)\cdot\left(\begin{matrix}B_x \\ B_y \\ B_z\end{matrix}\right)

Debe recalcarse que la matriz es la representación del tensor, pero no es el tensor, del mismo modo que un vector no son sus tres componentes, ya que éstas pueden cambiar en una transformación de coordenadas o en un cambio de ejes, aunque el vector siga siendo el mismo.

3 Propiedades del producto diádico

3.1 Linealidad

El producto diádico, así definido, es lineal respecto a los dos vectores que lo forman, esto es

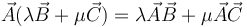
\vec{A}(\lambda\vec{B}+\mu\vec{C})=\lambda \vec{A}\vec{B}+\mu\vec{A}\vec{C}
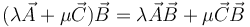
(\lambda\vec{A}+\mu\vec{C})\vec{B}=\lambda \vec{A}\vec{B}+\mu\vec{C}\vec{B}

Esta propiedad no es exclusiva de este producto. También el producto escalar y el vectorial la satisfacen.

3.2 Simetría o antisimetría

A diferencia del producto escalar, que es conmutativo, y del vectorial, que es anticonmutativo, el producto diádico no será, en general, ni una cosa ni la otra. Es facil ver por qué: el producto AxBy no tiene por que coincidir con AyBx. Así pues

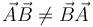
\vec{A}\vec{B}\neq\vec{B}\vec{A}

3.3 Traza

La traza del producto diádico se define como la suma de los elementos diagonales. Se deduce entonces que

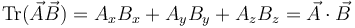
\mathrm{Tr}(\vec{A}\vec{B})=A_xB_x+A_yB_y+A_zB_z=\vec{A}\cdot\vec{B}

3.4 Producto escalar de una diada por un vector

Puede multiplicarse escalarmente una diada por otro vector análogamente a como una matriz 3\times3 se multiplica por un vector columna. Resulta entonces

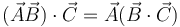
(\vec{A}\vec{B})\cdot\vec{C}=\vec{A}(\vec{B}\cdot\vec{C})

Nótese el diferente carácter de los términos de esta expresión. En el primer miembro tenemos el producto de un tensor por un vector; en el segundo, el de un vector por un escalar. Nótese tambien la posición del punto.

Tenemos pues que el producto de una diada por un vector da otro vector que, en general, tendrá una dirección y un módulo diferente al original. De hecho, esta definición permite definir las diadas en una forma abstracta, independiente del sistema de coordenadas elegido, en forma de un operador vectorial.

3.5 Otros productos

Igualmente se puede multiplicar un vector escalarmente por la derecha

\vec{C}\cdot(\vec{A}\vec{B})\equiv (\vec{C}\cdot\vec{A})\vec{B}

(obsérvese que el resultado cambia según el lado por el que se multiplique).

También se puede multiplicar simultaneamente por ambos lados. En este caso, el resultado es un número.

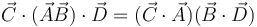
\vec{C}\cdot(\vec{A}\vec{B})\cdot\vec{D}=(\vec{C}\cdot\vec{A})(\vec{B}\cdot\vec{D})

Asimismo se puede multiplicar vectorialmente

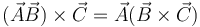
(\vec{A}\vec{B})\times\vec{C}=\vec{A}(\vec{B}\times\vec{C})

en este caso, el resultado es otra diada. En general, todos los productos definidos sobre vectores son generalizables a diadas.

4 Base de las diadas

De la propiedad de linealidad resulta de forma inmediata que

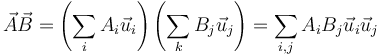
\vec{A}\vec{B}=\left(\sum_iA_i\vec{u}_i\right)\left(\sum_kB_j\vec{u}_j\right)= \sum_{i,j}A_iB_j\vec{u}_i\vec{u}_j

por lo que, conocidos los productos diádicos de los vectores de la base, podemos expresar cualquier diada en función de ellos. Por su parte, se tiene que, por ejemplo,

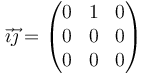
\vec{\imath}\vec{\jmath}=\left(\begin{matrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right)

En general, el producto de dos vectores unitarios en cartesianas puede representarse, en forma matricial, como una matriz con un elemento unitario y los demás nulos. Por ello, podemos concluir que los productos diádicos de los vectores unitarios forman un sistema generador del conjunto de las diadas.

5 Tensores cartesianos

Partiendo de la analogía tensor/matriz puede extenderse lo dicho a todos los tensores, esto es, cualquier tensor puede expresarse como combinación lineal de diadas unitarias. En forma algebraica

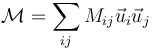
\mathcal{M}=\sum_{ij}M_{ij}\vec{u}_i\vec{u}_j

donde los Mij son los elementos de la matriz que representa al tensor en coordenadas cartesianas.

Es inmediato que las definiciones y propiedades del álgebra matricial pueden expresarse asimismo en su forma diádica.

5.1 Tensor unidad (o identidad)

Un tensor especialmente importante es el unitario, que se caracteriza por que todos los elementos de la diagonal valen la unidad y el resto son nulos. Se sigue que

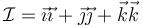
\mathcal{I}=\vec{\imath}\vec{\imath}+\vec{\jmath}\vec{\jmath}+\vec{k}\vec{k}

Puede comprobarse que se trata del tensor identidad viendo como actúa sobre un vector arbitario

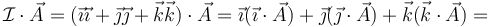
\mathcal{I}\cdot\vec{A}=(\vec{\imath}\vec{\imath}+\vec{\jmath}\vec{\jmath}+\vec{k}\vec{k})\cdot \vec{A}=\vec{\imath}(\vec{\imath}\cdot\vec{A})+\vec{\jmath}(\vec{\jmath}\cdot\vec{A})+\vec{k}(\vec{k}\cdot\vec{A})=
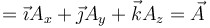
=\vec{\imath}A_x+\vec{\jmath}A_y+\vec{k}A_z=\vec{A}

6 Cambios de base

Con lo dicho hasta ahora no se evidencia ninguna ventaja de la expresión diádica de un tensor sobre la expresión matricial. Estas aparecen cuando se considera que mientras que la última es válida sólo en coordenadas cartesianas, la primera es manejable tanto en su forma abstracta como en cualquier sistema.

Consideremos, por ejemplo, la diada

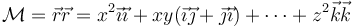
\mathcal{M}=\vec{r}\vec{r}=x^2\vec{\imath}\vec{\imath}+xy(\vec{\imath}\vec{\jmath}+\vec{\jmath}\vec{\imath})+\cdots+ z^2\vec{k}\vec{k}

Tanto esta expresión como la matricial tienen nueve componentes no nulas. Sin embargo, si empleamos coordenadas esféricas queda

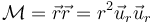
\mathcal{M}=\vec{r}\vec{r}=r^2\vec{u}_r\vec{u}_r

esto es, sólo una componente es no nula y, por tratarse del mismo tensor (que, recordemos, es independiente del sistema de coordenadas) es mucho más fácil trabajar con esta expresión.

Hay que remarcar que, cuando se usan coordenadas no cartesianas, la expresión matricial del tensor carece de utilidad (en cuanto que no se va a comportar como lo hacen las matrices “normales”).

En particular la expresión del tensor identidad en cualquier base ortogonal es

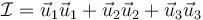
\mathcal{I}=\vec{u}_{1}\vec{u}_{1}+\vec{u}_{2}\vec{u}_{2}+\vec{u}_{3}\vec{u}_{3}

Para realizar el cambio de un sistema de coordenadas a otro las reglas de transformación son análogas a las que se aplican entre vectores, sólo hay que aplicarlas a cada uno de los vectores unitarios que componen las diadas. Por ejemplo

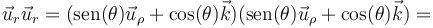
\vec{u}_r\vec{u}_r=(\mathrm{sen}(\theta)\vec{u}_{\rho}+\cos(\theta)\vec{k})(\mathrm{sen}(\theta)\vec{u}_{\rho}+\cos(\theta)\vec{k})=
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): = \sen^2\theta\vec{u}_{\rho}\vec{u}_{\rho}+\mathrm{sen}(\theta)\cos(\theta)(\vec{u}_{\rho}\vec{k}+\vec{k}\vec{u}_{\rho})+\cos^2\theta\vec{k}\vec{k}

Es posible también construir una base del espacio de los tensores combinando dos bases vectoriales diferentes (por ejemplo, construyendo los productos 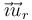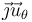\vec{\imath}\vec{u}_r, \vec{\jmath}\vec{u}_{\theta} y similares), pero no suele ser de mucha utilidad.


7 Diadas aplicadas a la física

La introducción de las diadas no pasaría de se un simple juego matemático si no sirvieran para simplificar las leyes físicas. En la física aparecen frecuentemente tensores cartesianos, todos los cuales admiten la expresión diádica correspondiente. En algunos caso ésta es más simple que las expresiones matriciales correspondientes. Veamos tres ejemplos, dos de mecánica y uno de electromagnetismo.

7.1 Matrices de rotación

7.2 Tensor de inercia

Cuando se estudia el sólido rígido, se introduce el tensor de inercia 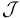\mathcal{J} que, para un punto material, es una matriz con componentes

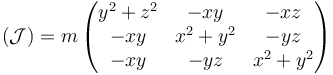
(\mathcal{J})=m\left(\begin{matrix}y^2+z^2 & -xy & -xz \\ -xy & x^2+y^2 & -yz \\ -xy & -yz & x^2+y^2\end{matrix}\right)

En forma diádica este tensor se escribe simplemente como

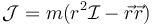
\mathcal{J}=m(r^2\mathcal{I}-\vec{r}\vec{r})

Usando la expresión diádica podemos obtener, por ejemplo, el valor del momento angular

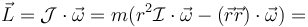
\vec{L}=\mathcal{J}\cdot\vec{\omega}=m(r^2\mathcal{I}\cdot\vec{\omega}-(\vec{r}\vec{r})\cdot\vec{\omega})=
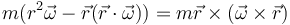
m(r^2\vec{\omega}-\vec{r}(\vec{r}\cdot\vec{\omega}))=m\vec{r}\times(\vec{\omega}\times\vec{r})

Si lo que queremos es hallar el tensor de inercia de una distribución tendremos que

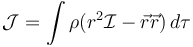
\mathcal{J}=\int \rho (r^2\mathcal{I}-\vec{r}\vec{r})\,d\tau

También podemos obtener el tensor de inercia para una partícula en coordenadas esféricas como

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathcal{J}=m(r^2(\vec{u}_r\vec{u}_r+\vec{u}_{\theta}\vec{u}_{\theta}+\vec{u}_{\vp}\vec{u}_{\vp})- (r^2\vec{u}_r\vec{u}_r))=
No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): = mr^2(\vec{u}_{\theta}\vec{u}_{\theta}+\vec{u}_{\vp}\vec{u}_{\vp})

7.3 Tensor de tensiones

8 …y más allá

Hasta aquí hemos hablado de las diadas como un producto entre dos vectores y lo hemos aplicado al estudio de los tensores cartesianos de segundo orden exclusivamente. Sin embargo, todo lo dicho no es más que un caso particular de un producto tensorial, extensible a cualquier orden y cualquier métrica. No existe problema en definir el producto diádico de tres vectores 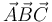\vec{A}\vec{B}\vec{C} que sería un tensor de tercer orden, imposible de representar por una matriz. También es posible tratar las diadas como un caso particular de aplicación lineal sobre los vectores. Cabe entonces hablar de diadas duales, de coordenadas covariantes y contravariantes, etc. Para todo ello existe bibliografía disponible.

Obtenido de "http://tesla.us.es/wiki/index.php/Diadas_y_productos_di%C3%A1dicos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace