Centro de masas en sistemas de esferas

De Laplace

(Diferencias entre revisiones)

última version al 13:44 1 jul 2019

Contenido

1 Enunciado
2 Dos esferas adyacentes
- 2.1 Masas
- 2.2 Centro de masas
3 Una esfera con hueco
- 3.1 Masa total
- 3.2 Centro de masas

1 Enunciado

Se tienen dos esferas macizas del mismo material de densidad homogénea, $ρ 0$ , una de ellas de radio $2 b$ y la otra de radio $b$ . Las dos esferas son adyacentes. Determine la posición del centro de masas del sistema.

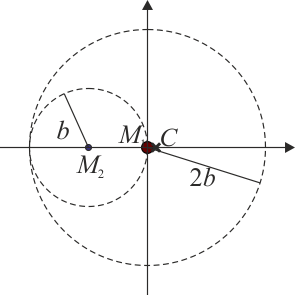
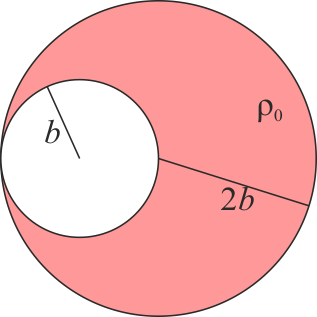
Si en lugar del sistema anterior se tiene una sola esfera maciza de radio $2 b$ y densidad homogénea $ρ 0$ en la que se ha horadado una cavidad también esférica, de radio $b$ , cuyo centro se encuentra a una distancia $b$ del centro de la esfera original ¿dónde se halla el centro de masas del sólido?

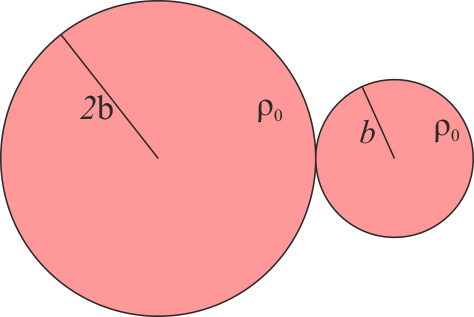
2 Dos esferas adyacentes

El centro de masas de un sistema de partículas se calcula mediante la expresión

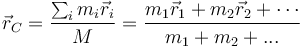
$\vec{r}_C=\frac{\sum_i m_i\vec{r}_i}{M}=\frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{m_1+m_2+...}$

En el caso de que tengamos una distribución continua, esta fórmula se sustituye por la correspondiente integral

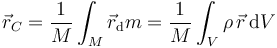
$\vec{r}_C=\frac{1}{M}\int_M \vec{r}_\mathrm{d}m = \frac{1}{M}\int_V \rho\,\vec{r}\,\mathrm{d}V$

En principio, para calcular el centro de masas del conjunto de las dos esferas debemos hacer la integral sobre el volumen completo. Sin embargo, el problema se simplifica si lo descomponemos en las dos partes que lo componen.

2.1 Masas

En primer lugar tenemos que la masa total del conjunto es la suma de las masas de cada una de las esferas

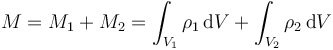
$M = M_1+M_2 = \int_{V_1}\rho_1\,\mathrm{d}V+\int_{V_2}\rho_2\,\mathrm{d}V$

En este caso las dos densidades son homogéneas (independientes de la posición) e iguales en las dos esferas, por lo que

$M_1 = \int_{V_1}\rho_1\,\mathrm{d}V = \rho_0V_1 = \frac{4\pi}{3}\rho_0(2b)^3\qquad\qquad M_2 = \int_{V_2}\rho_2\,\mathrm{d}V = \rho_0V_2 = \frac{4\pi}{3}\rho_0b^3=\frac{M_1}{8}$

siendo la masa total

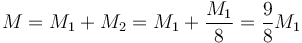
$M=M_1+M_2=M_1+\frac{M_1}{8}=\frac{9}{8}M_1$

2.2 Centro de masas

Para el numerador que aparece en el centro de masas realizamos una descomposición similar y nos queda

$M\vec{r}_c = \int_{V}\rho\,\vec{r}\,\mathrm{d}V = \int_{V_1}\rho_1\,\vec{r}\,\mathrm{d}V+\int_{V_2}\rho_2\,\vec{r}\,\mathrm{d}V$

Ahora bien, los centros de masas de cada una de las esferas por separado verifican

$\vec{r}_{C1}=\frac{1}{M_1}\int_{V_1}\rho_1\vec{r}\mathrm{d}V\qquad\qquad \vec{r}_{C2}=\frac{1}{M_2}\int_{V_2}\rho_1\vec{r}\mathrm{d}V$

y por tanto

$M\vec{r}_C=M_1\vec{r}_{C1}+M_2\vec{r}_{C2}\qquad\Rightarrow\qquad \vec{r}_{C}=\frac{M_1\vec{r}_{C1}+M_2\vec{r}_{C2}}{M_1+M_2}$

es decir, el centro de masas de la figura completa se puede hallar considerándola compuesta por solo dos partículas, cada una de las cuales tiene la masa de cada parte y se encuentra en el centro de masas de cada una. Esto es válido independientemente de que se trate de esferas o de cualquier otra figura o división que se haga en el sistema.

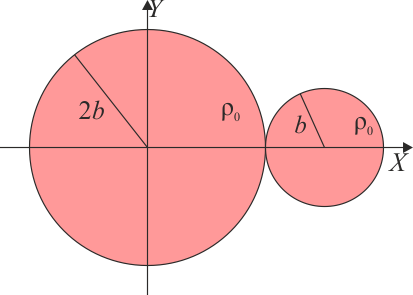
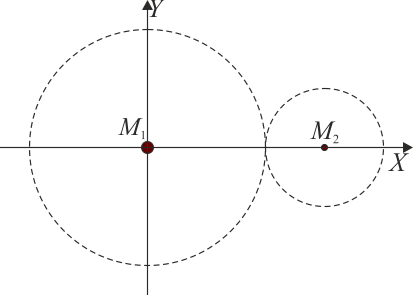
Por tratarse de esferas homogéneas, el centro de masas de cada una se halla en su centro. Considerando un sistema de ejes centrado en la esfera grande y con el eje OX sobre la recta que pasa por los dos centros queda

$\vec{r}_{C1}=\vec{0}\qquad\qquad \vec{r}_{C2}=3b\vec{\imath}$

y resulta para la posición del centro de masas del sistema

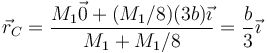
$\vec{r}_C = \frac{M_1\vec{0}+ (M_1/8)(3b)\vec{\imath}}{M_1+M_1/8}=\frac{b}{3}\vec{\imath}$

Vemos que este punto no se halla a mitad de camino de los dos centros, sino mucho más cerca del centro de la esfera grande, que contribuye ocho veces más al total del sistema.

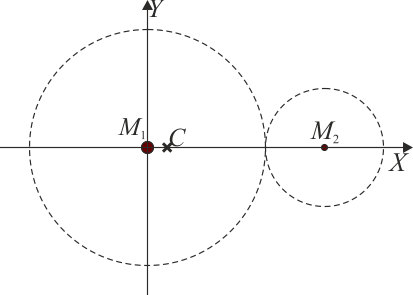
3 Una esfera con hueco

Para el caso de la esfera con hueco parece que tenemos un solo sistema, por lo que la técnica de la descomposición en dos o más partes no parece aplicable. Sin embargo, sí podemos hacerlo. ¿Cómo? Empleando masas negativas.

3.1 Masa total

Consideremos la masa total del sistema. Esta se calcula mediante la integral

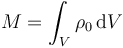
$M = \int_V \rho_0\,\mathrm{d}V$

donde la integral se extiende a todo el volumen donde hay masa (la esfera, descontándole el hueco). Dicho de otra forma, esta integral se puede escribir como la integral, extendida a la esfera completa, pero con una densidad tal que

$\rho(\vec{r})=\begin{cases}\rho_0 & \mbox{fuera del hueco} \\ 0 & \mbox{dentro del hueco}\end{cases}$

Esta integral se puede escribir, como antes, como suma de dos

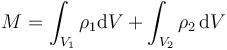
$M = \int_{V_1}\rho_1 \mathrm{d}V + \int_{V_2}\rho_2\,\mathrm{d}V$

donde el primer volumen es la esfera grande completa, como si no tuviera hueco, y $V 2$ es el volumen del hueco. Vemos que de esta forma estamos contando el volumen del hueco dos veces. ¿Qué densidad debemos asignar a cada una de las integrales para que el resultado coincida con el anterior? Pues

$\rho_1 = \rho_0\qquad\qquad \rho_2 = -\rho_0$

De esta forma

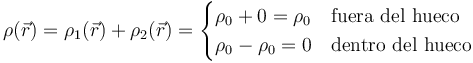
$\rho(\vec{r})=\rho_1(\vec{r})+\rho_2(\vec{r}) = \begin{cases}\rho_0+0 = \rho_0& \mbox{fuera del hueco} \\ \rho_0-\rho_0 = 0 & \mbox{dentro del hueco}\end{cases}$

Por tanto el sistema se puede modelar como dos esferas superpuestas, una de ellas con densidad de carga negativa. Este es un procedimiento habitual con densidades de carga, que pueden ser de los dos signos, pero también es aplicable a masas.

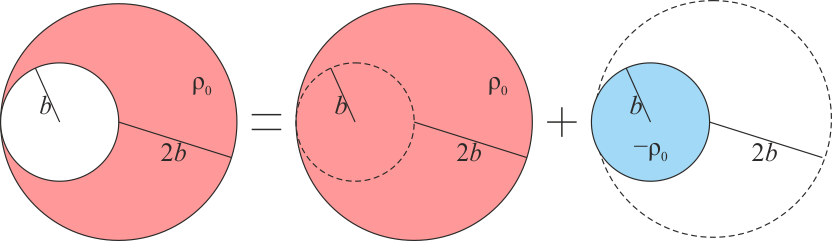
De esta forma, las masas individuales valen

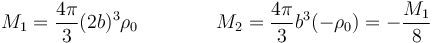
$M_1 = \frac{4\pi}{3}(2b)^3\rho_0 \qquad\qquad M_2 = \frac{4\pi}{3}b^3(-\rho_0) = -\frac{M_1}{8}$

siendo la masa total

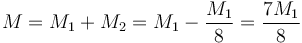
$M = M_1+M_2 = M_1-\frac{M_1}{8}=\frac{7M_1}{8}$

Naturalmente la masa total es menor que la que tendría una esfera maciza, pues le estamos descontando el hueco.

3.2 Centro de masas

La superposición anterior puede aplicarse también al centro de masas, de forma que tenemos, como en el caso de las dos esferas

$\vec{r}_C = \frac{M_1\vec{r}_{C1}+M_2\vec{r}_{C2}}{M_1+M_2}$

donde ahora los centros de masas de las dos esferas se encuentran en

$\vec{r}_{C1}=\vec{0}\qquad\qquad \vec{r}_{C2}=-b\vec{\imath}$

resultando la posición del centro de masas del sistema

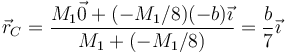
$\vec{r}_C = \frac{M_1\vec{0}+(-M_1/8)(-b)\vec{\imath}}{M_1+(-M_1/8)}= \frac{b}{7}\vec{\imath}$

El centro de masas se halla en el semieje positivo, ya que en ese lado es el que se concentra la mayor parte de la masa.

@@ Línea 7: / Línea 7: @@
 ==Dos esferas adyacentes==
-El centro de masas de un sistema de partículas se calcula mediante la expreisón
+El centro de masas de un sistema de partículas se calcula mediante la expresión
 <center><math>\vec{r}_C=\frac{\sum_i m_i\vec{r}_i}{M}=\frac{m_1\vec{r}_1+m_2\vec{r}_2+\cdots}{m_1+m_2+...}</math></center>

Centro de masas en sistemas de esferas

De Laplace

última version al 13:44 1 jul 2019

Contenido

1 Enunciado

2 Dos esferas adyacentes

2.1 Masas

2.2 Centro de masas

3 Una esfera con hueco

3.1 Masa total

3.2 Centro de masas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES