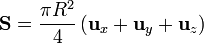Vector superficie

De Laplace

Contenido

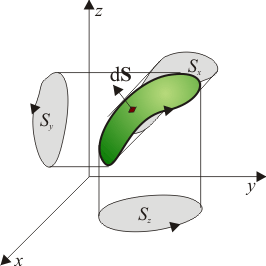
1 Vector diferencial de superficie
2 Vector superficie
- 2.1 Caso de una superficie plana
- 2.2 Caso de una curva alabeada
3 Expresión como integral de camino
4 Ejemplo
5 Enlaces

1 Vector diferencial de superficie

Cuando tenemos una superficie suave, la definición del vector diferencial de superficie es sencilla:

$\mathrm{d}\mathbf{S}=\mathrm{d}S\,\mathbf{n}$

donde $d S$ es el área del elemento de superficie y $\mathbf{n}$ es el vector normal a la superficie en el punto en que se encuentra el diferencial. O, para ser más precisos, el vector normal al plano tangente a dicha superficie en dicho punto

2 Vector superficie

dada una superficie $S$ de extensión finita, definimos el vector superficie como

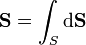
$\mathbf{S}=\int_S\mathrm{d}\mathbf{S}$

Ahora bien, aunque la definición es simple, la interpretación no lo es tanto. ¿Qué representa geométricamente este vector? ¿Cuánto vale su módulo? ¿En qué dirección apunta?

2.1 Caso de una superficie plana

Si la superficie $S$ está contenida en un plano, la interpretación del vector 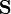$\mathbf{S}$ es inmediata. El plano tangente en todos los puntos es el mismo: el que contiene a $S$ , y por tanto el vector $\mathbf{n}$ es constante y puede salir de la integral

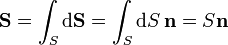
$\mathbf{S}=\int_S\mathrm{d}\mathbf{S}=\int_S\mathrm{d}S\,\mathbf{n}=S\mathbf{n}$

esto es, para el caso de una superficie contenida en un plano, el vector superficie tiene por módulo el área de dicha superficie, y por dirección la normal al plano que la contiene.

2.2 Caso de una curva alabeada

Si tenemos una curva alabeada, esto es, que no puede ser contenida en un plano, el cálculo anterior ya no es posible. El vector normal depende de la posición y por tanto debe ser integrado. Esto hace que la dirección del vector resultante no sea conocida a priori, y que su módulo no sea igual al área de la superficie.

3 Expresión como integral de camino

3.1 Expresión general

Existe una forma alternativa de calcular el vector superficie. Sea $Γ$ la curva que delimita dicha superficie. Se verifica que

$\mathbf{S}=\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r}$

donde $Γ$ ha de recorrerse de forma que verifique la regla de la mano derecha con respecto al vector normal a 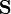$\mathbf{S}$ .

Antes de proceder a la demostración de esta fórmula, un par de observaciones sobre ella:

Todas las superficies apoyadas sobre la misma curva tendrán el mismo vector superficie.

El vector superficie para una superficie cerrada es el vector nulo.

3.2 Caso de una curva plana

3.2.1 Sobre un plano coordenado

Supongamos, en primer lugar, que tenemos una curva plana, sobre la que situamos el plano $X Y$ . En este plano

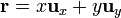
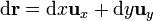
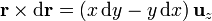
$\mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y$ $\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_x+\mathrm{d}y\mathbf{u}_y$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)\mathbf{u}_z$

El módulo de la integral es por tanto igual a

$\left|\mathbf{I}\right| = \left| \frac{1}{2}\oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right|=\frac{1}{2}\oint_\Gamma \left(-y\,\mathrm{d}x+x\,\mathrm{d}y\right)$

Esta integral puede escribirse como una circulación

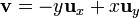
$\left|\mathbf{I}\right| = \frac{1}{2}\oint_\Gamma \mathbf{v}\cdot\mathrm{d}\mathbf{r}$ $\mathbf{v}=-y\mathbf{u}_x+x\mathbf{u}_y$

Podemos entonces aplicar el teorema de Stokes

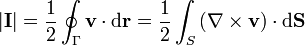
$\left|\mathbf{I}\right| = \frac{1}{2}\oint_\Gamma \mathbf{v}\cdot\mathrm{d}\mathbf{r} = \frac{1}{2}\int_S\left(\nabla\times\mathbf{v}\right)\cdot\mathrm{d}\mathbf{S}$

siendo el rotacional

$\nabla\times\mathbf{v} = \left|\begin{matrix}\mathbf{u}_x & \mathbf{u}_x & \mathbf{u}_x \\ & & \\ \displaystyle\frac{\partial\ }{\partial x} &\displaystyle\frac{\partial\ }{\partial y} & \displaystyle\frac{\partial\ }{\partial z} \\ & & \\ -y & x & 0\end{matrix}\right| = 2\mathbf{u}_z$

y el diferencial de superficie, por estar ésta en el plano XY

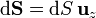
$\mathrm{d}\mathbf{S} = \mathrm{d}S\,\mathbf{u}_z$

con lo que queda finalmente

$\left|\mathbf{I}\right| = \left| \frac{1}{2}\oint_{\Gamma} \mathbf{r} \times \mathrm{d}\mathbf{r}\,\right|= \frac{1}{2}\int_S\left(\nabla\times\mathbf{v}\right)\cdot\mathrm{d}\mathbf{S}= \frac{1}{2}\int_S\left(2\mathbf{u}_z\right)\cdot\left(\mathrm{d}\mathbf{S}\right) = \int_S \mathrm{d}S = S$

y en cuanto a la dirección, la integral apunta en la dirección del eje $Z$ . Por tanto, para el caso de una curva plana resulta un vector que tiene por módulo el área de la superficie que define, y por dirección la normal al plano, que son las dos propiedades que definen al vector superficie en este caso. En el caso de una curva en el plano XY tenemos entonces que

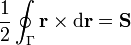
$\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r} = \mathbf{S}$

3.2.2 Interpretación geométrica

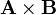Este resultado se puede obtener de forma sencilla usando exclusivamente álgebra vectorial. Dados dos vectores $\mathbf{A}$ y $\mathbf{B}$ , su producto vectorial $\mathbf{A}\times\mathbf{B}$ es un vector ortogonal a ambos y cuyo módulo es el área del paralelogramo definido por ambos vectores. El vector

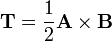
$\mathbf{T}=\frac{1}{2}\mathbf{A}\times\mathbf{B}$

será por tanto un vector ortogonal a ambos y con módulo el área de un triángulo definido por estos dos vectores.

Si consideramos el vector diferencial

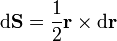
$\mathrm{d}\mathbf{S}=\frac{1}{2}\mathbf{r}\times\mathrm{d}\mathbf{r}$

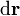obtendremos un vector de módulo el diferencial de área triangular, y por dirección la normal al plano definido por $\mathbf{r}$ y $\mathrm{d}\mathbf{r}$ . Para el caso de una curva contenida en el plano $z = 0$ esta dirección es constante y dada por $\mathbf{u}_z$ .

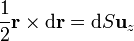
$\frac{1}{2}\mathbf{r}\times\mathrm{d}\mathbf{r}=\mathrm{d}S\mathbf{u}_z$

Integrando sobre una curva cerrada sumamos las áreas de todos los triángulos diferenciales, resultando el área total

$\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r}=\int_S \mathrm{d}S\mathbf{u}_z = S\mathbf{u}_z$

3.2.3 Curva plana en el espacio

Veamos ahora el caso de una curva tridimensional que sí puede ser contenida en un plano, aunque éste no coincida con ninguno de los planos coordenados.

Los puntos de esta curva verifican la ecuación vectorial del plano

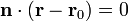
$\mathbf{n}\cdot\left(\mathbf{r}-\mathbf{r}_0\right) = 0$

siendo $\mathbf{n}$ el vector unitario normal al plano y $\mathbf{r}_0$ un punto dado de éste. Podemos escribir entonces la curva como

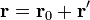
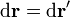
$\mathbf{r}=\mathbf{r}_0+\mathbf{r}'$ $\mathrm{d}\mathbf{r} = \mathrm{d}\mathbf{r}'$

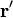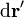donde tanto $\mathbf{r}'$ como $\mathrm{d}\mathbf{r}'$ son vectores ortogonales a $\mathbf{n}$ . Sustituyendo en la expresión del vector superficie

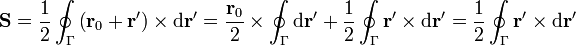
$\mathbf{S}=\frac{1}{2}\oint_\Gamma \left(\mathbf{r}_0+\mathbf{r}'\right)\times\mathrm{d}\mathbf{r}'=\frac{\mathbf{r}_0}{2}\times\oint_\Gamma\mathrm{d}\mathbf{r}'+\frac{1}{2}\oint_\Gamma\mathbf{r}'\times\mathrm{d}\mathbf{r}'=\frac{1}{2}\oint_\Gamma\mathbf{r}'\times\mathrm{d}\mathbf{r}'$

En la primera integral $\mathbf{r}_0$ puede salir de la integral por ser un vector constante, con lo que queda una integral de una diferencial exacta sobre una curva cerrada, que se anula.

Este resultado nos dice que el vector superficie es independiente del origen de coordenadas elegido. Este resultado es válido tanto si la curva es plana como si es alabeada.

Si lo que tenemos es una curva plana, de acuerdo con lo que se vio en el primer apartado

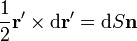
$\frac{1}{2}\mathbf{r}'\times\mathrm{d}\mathbf{r}' = \mathrm{d}S\mathbf{n}$

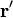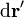siendo $d S$ el área del triángulo diferencial definido por $\mathbf{r}'$ y $\mathrm{d}\mathbf{r}'$ y $\mathbf{n}$ el vector normal al plano que contiene a ambos vectores. Por tanto el vector superficie es

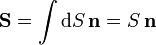
$\mathbf{S}=\int \mathrm{d}S\,\mathbf{n}=S\,\mathbf{n}$

esto es, para una curva plana, independientemente de cual sea su orientación, el vector superficie tiene por módulo el área de la sección de plano que define, por dirección la normal a dicho plano y por sentido el dado por la regla de la mano derecha.

3.3 Caso de una curva alabeada

Supongamos ahora que tenemos una curva alabeada, esto es, que no puede contenerse en un plano, o una curva plana pero que no está situada en ninguno de los planos coordenados.

3.3.1 Demostración

Vamos a probar el caso general. Para una curva cualquiera $Γ$ (alabeada o plana) veremos que

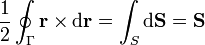
$\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r} = \int_S \mathrm{d}\mathbf{S} = \mathbf{S}$

donde $S$ es una superficie arbitraria apoyada en $Γ$ y orientada según la regla de la mano derecha.

Sea $\mathbf{A}$ un vector arbitrario constante. Si multiplicamos el primer miembro por este vector y aplicamos las propiedades del producto mixto

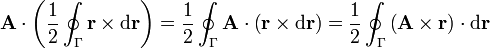
$\mathbf{A}\cdot\left(\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r}\right) = \frac{1}{2}\oint_\Gamma \mathbf{A}\cdot\left(\mathbf{r}\times\mathrm{d}\mathbf{r}\right)=\frac{1}{2}\oint_\Gamma \left(\mathbf{A}\times\mathbf{r}\right)\cdot\mathrm{d}\mathbf{r}$

Esta última integral es una circulación, a la que se puede aplicar el teorema de Stokes

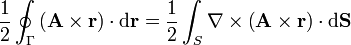
$\frac{1}{2}\oint_\Gamma \left(\mathbf{A}\times\mathbf{r}\right)\cdot\mathrm{d}\mathbf{r} = \frac{1}{2}\int_S \nabla\times\left(\mathbf{A}\times\mathbf{r}\right)\cdot\mathrm{d}\mathbf{S}$

Según se ve en un problema sobre algunas identidades vectoriales, para un vector constante $\mathbf{A}$

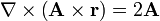
$\nabla\times\left(\mathbf{A}\times\mathbf{r}\right) = 2\mathbf{A}$

así que nos queda

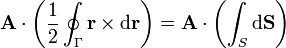
$\mathbf{A}\cdot\left(\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r}\right) = \mathbf{A}\cdot\left(\int_S \mathrm{d}\mathbf{S}\right)$

Esta identidad se cumple sea cual sea el vector $\mathbf{A}$ , lo cual solo es posible si

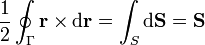
$\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r} = \int_S \mathrm{d}\mathbf{S} = \mathbf{S}$

como queríamos demostrar.

3.3.2 Interpretación de las componentes

En una curva tridimensional, tanto el vector de posición como el diferencial de camino poseen las tres componentes

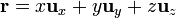
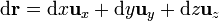
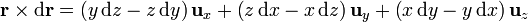
$\mathbf{r}=x\mathbf{u}_x+y\mathbf{u}_y+z\mathbf{u}_z$ $\mathrm{d}\mathbf{r}=\mathrm{d}x\mathbf{u}_x+\mathrm{d}y\mathbf{u}_y+\mathrm{d}z\mathbf{u}_z$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=\left(y\,\mathrm{d}z-z\,\mathrm{d}y\right)\mathbf{u}_x+\left(z\,\mathrm{d}x-x\,\mathrm{d}z\right)\mathbf{u}_y+\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)\mathbf{u}_z$

Al sustituir en la integral nos resulta la suma de tres términos

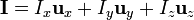
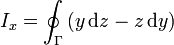
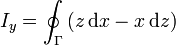
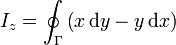
$\mathbf{I}=I_x\mathbf{u}_x+I_y\mathbf{u}_y+I_z\mathbf{u}_z$ $I_x=\oint_\Gamma\left(y\,\mathrm{d}z-z\,\mathrm{d}y\right)$ $I_y=\oint_\Gamma\left(z\,\mathrm{d}x-x\,\mathrm{d}z\right)$ $I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)$

Si nos fijamos, por ejemplo, en la tercera componente

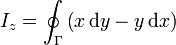
$I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)$

vemos que el integrando es exactamente el mismo que en el caso de una curva plana. La curva de integración en este caso es tridimensional, pero, puesto que en el integrando aparecen solamente $x$ e $y$ , realmente los valores de $z$ son irrelevantes. Otra curva, con diferentes valores de $z$ , en particular, una curva que tuviera $z = 0$ , pero los mismos valores de $x$ e $y$ , daría el mismo resultado. Esto es, que esta componente es igual a la integral sobre la proyección de la curva $Γ$ en el plano $X Y$ . La proyección es una curva plana, y por tanto, para ella es aplicable el resultado del apartado anterior. Por tanto

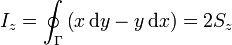
$I_z=\oint_\Gamma\left(x\,\mathrm{d}y-y\,\mathrm{d}x\right)=2S_z$

siendo $S z$ el área de la proyección de $Γ$ sobre el plano $z = 0$

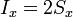
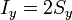
De la misma manera se interpretan las otras dos componentes $I_x = 2S_x\,$ $I_y=2S_y\,$

o, reuniendo los tres resultados

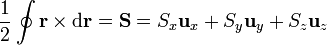
$\frac{1}{2}\oint\mathbf{r}\times\mathrm{d}\mathbf{r} = \mathbf{S}=S_x\mathbf{u}_x+S_y\mathbf{u}_y+S_z\mathbf{u}_z$

Siendo el vector superficie uno que tiene por componentes las áreas de las proyecciones de la curva $Γ$ sobre los tres planos coordenados.

En cuanto al signo de estas componentes, viene dado por la regla de la mano derecha. Si recorremos la proyección en $z = 0$ de tal forma que el vector normal (según esta regla) vaya en el mismo sentido que $\mathbf{u}_z$ , entonces el signo es positivo. En caso contrario es negativo.

Para el caso de una curva plana en un plano arbitrario, dado que el vector $\mathbf{n}$ tiene por componentes cartesianas los cosenos directores (cosenos de los ángulos que forma con cada eje)

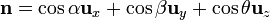
$\mathbf{n}=\cos\alpha\mathbf{u}_x+\cos\beta\mathbf{u}_y+\cos\theta\mathbf{u}_z$

resulta, para las componentes del vector superficie

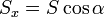
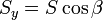
$S_x = S\cos\alpha\,$ $S_y=S\cos\beta\,$ $S_z=S\cos\theta\,$

4 Ejemplo

4.1 Integración del diferencial de superficie

Consideremos una superficie en forma de octante de esfera de radio $R$ . Una extensión ingenua del caso plano podría sugerir que el vector superficie es igual al área del octante ( $4π R 2 / 8$ ), multiplicado por el vector normal que sería 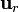$\mathbf{u}_r$ . Sin embargo, este resultado es incorrecto, pues 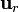$\mathbf{u}_r$ es dependiente de la posición y tiene significado para cada punto, pero no cuando consideramos la superficie como un todo.

Veamos cuánto sería el resultado correcto. Por tratarse se una superficie esférica, tenemos que

$\mathrm{d}\mathbf{S}=R^2\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\mathbf{u}_r$ $0<\theta<\frac{\pi}{2}\qquad 0<\varphi<\frac{\pi}{2}$ $\mathbf{u}_r=\mathrm{sen}\,\theta\cos\varphi\mathbf{u}_x+\mathrm{sen}\,\theta\,\mathrm{sen}\,\varphi\mathbf{u}_y+\cos\theta\mathbf{u}_z$

Sustituyendo todo esto nos quedan las componentes

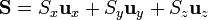
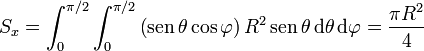
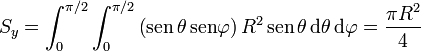
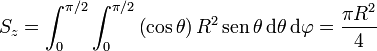
$\mathbf{S}=S_x\mathbf{u}_x+S_y\mathbf{u}_y+S_z\mathbf{u}_z$ $S_x = \int_0^{\pi/2}\int_0^{\pi/2}\left(\mathrm{sen}\,\theta\cos\varphi\right)R^2\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi = \frac{\pi R^2}{4}$ $S_y = \int_0^{\pi/2}\int_0^{\pi/2}\left(\mathrm{sen}\,\theta\,\mathrm{sen}\varphi\right)R^2\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi = \frac{\pi R^2}{4}$ $S_z = \int_0^{\pi/2}\int_0^{\pi/2}\left(\cos\theta\right)R^2\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi = \frac{\pi R^2}{4}$

y, reuniendo las tres componentes

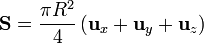
$\mathbf{S}=\frac{\pi R^2}{4}\left(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z\right)$

4.2 Cálculo de la integral de camino

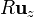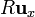Si el resultado anterior lo calculamos a partir de la integral curvilínea, tenemos tres sumandos, uno por cada arco circular. Para el que va desde $R\mathbf{u}_z$ a $R\mathbf{u}_x$ tenemos que 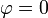$\varphi=0\,$ y recorremos la curva variando $θ$ de 0 a $π / 2$

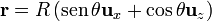
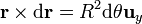
$\mathbf{r}=R\left(\mathrm{sen}\,\theta\mathbf{u}_x+\cos\theta\mathbf{u}_z\right)$ $\mathrm{d}\mathbf{r}=R\left(\cos\theta\mathbf{u}_x-\mathrm{sen}\,\theta\mathbf{u}_z\right)\mathrm{d}\theta$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=R^2\mathrm{d}\theta\mathbf{u}_y$

y la contribución de este tramo es

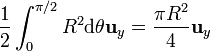
$\frac{1}{2}\int_0^{\pi/2}R^2\mathrm{d}\theta\mathbf{u}_y = \frac{\pi R^2}{4}\mathbf{u}_y$

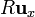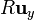Para el que va de $R\mathbf{u}_x$ a $R\mathbf{u}_y$ , $θ = π / 2$ y variamos $\varphi$ de 0 a $π / 2$

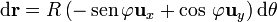
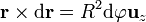
$\mathbf{r}=R\left(\cos\varphi\mathbf{u}_x+\mathrm{sen}\,\varphi\mathbf{u}_y\right)$ $\mathrm{d}\mathbf{r}=R\left(-\,\mathrm{sen}\,\varphi\mathbf{u}_x+\cos\,\varphi\mathbf{u}_y\right)\mathrm{d}\theta$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=R^2\mathrm{d}\varphi\mathbf{u}_z$

dando como resultado

$\frac{1}{2}\int_0^{\pi/2}R^2\mathrm{d}\varphi\mathbf{u}_z = \frac{\pi R^2}{4}\mathbf{u}_z$

Para el último tramo 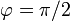$\varphi=\pi/2$ y variamos $θ$ de $π / 2$ a 0

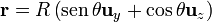
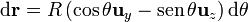
$\mathbf{r}=R\left(\mathrm{sen}\,\theta\mathbf{u}_y+\cos\theta\mathbf{u}_z\right)$ $\mathrm{d}\mathbf{r}=R\left(\cos\theta\mathbf{u}_y-\mathrm{sen}\,\theta\mathbf{u}_z\right)\mathrm{d}\theta$ $\mathbf{r}\times\mathrm{d}\mathbf{r}=-R^2\mathrm{d}\theta\mathbf{u}_x$

y la integral da

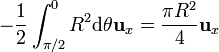
$-\frac{1}{2}\int_{\pi/2}^0R^2\mathrm{d}\theta\mathbf{u}_x = \frac{\pi R^2}{4}\mathbf{u}_x$

Sumando las tres contribuciones

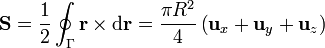
$\mathbf{S}=\frac{1}{2}\oint_\Gamma \mathbf{r}\times\mathrm{d}\mathbf{r} = \frac{\pi R^2}{4}\left(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z\right)$

4.3 Cálculo a partir de las proyecciones

La forma más simple de hallar este vector superficie es a partir de sus componentes cartesianas, calculadas como las proyecciones sobre los planos coordenados. Cada una de estas proyecciones es un cuarto de círculo de radio $R$ . El área de este sector circular es $π R 2 / 4$ . El vector superficie será entonces

$\mathbf{S}=\frac{\pi R^2}{4}\left(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z\right)$

5 Enlaces