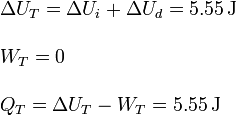Termómetro de gas

De Laplace

Contenido

1 Enunciado
2 Escala de temperaturas
3 Energía interna, calor y trabajo
4 Cálculo numérico de la temperatura
5 Cálculo numérico de calores, trabajos y variaciones de energía interna

1 Enunciado

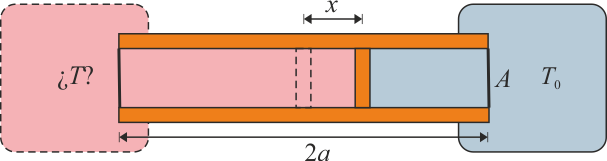
Se construye un termómetro de gas ideal según el siguiente principio: un tubo cilíndrico de sección $A$ y longitud $2 a$ con paredes adiabáticas y bases diatermas es dividido por un pistón, también adiabático, que puede deslizarse sin rozamiento por el interior del tubo. En el interior de las dos cámaras se encuentra un gas ideal. Una de las dos cámaras se mantiene en contacto térmico con un foco a temperatura $T 0$ , mientras que la otra se pone en contacto con el sistema cuya temperatura se quiere medir. Cuando las dos temperaturas son iguales el pistón se encuentra en la posición central y la presión del gas es $p 0$ .

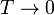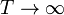Calcule la temperatura absoluta $T$ a la que se encuentra el sistema cuando el pistón se ha desplazado una cantidad $x$ desde el centro hacia el sistema a $T 0$ . ¿Resulta una escala lineal de temperaturas? ¿A cuánto tiende $x$ si $T\to 0$ o si $T\to\infty$ ?
Supongamos que se parte del equilibrio a $T 0$ y que la variación de la temperatura del gas de la cámara exterior y el desplazamiento del pistón en $x$ ha sido de forma cuasiestática y reversible. ¿Cuáles son los calores, trabajos e incrementos de energía interna para cada una de las cámaras y para el tubo completo, como función del desplazamiento $x$ del pistón?
Supongamos que el tubo mide 20 cm, la temperatura de referencia es 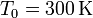$T_0 = 300\,\mathrm{K}$ y el pistón se desplaza 1 cm. ¿Cuál es la temperatura del sistema exterior?
Si además sabemos que la sección del tubo es de 10 cm², el gas contenido es aire y la presión inicial es 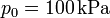$p_0 = 100\,\mathrm{kPa}$ , ¿cuánto valen los calores, trabajos e incrementos de energía interna del segundo apartado?

2 Escala de temperaturas

Nuestro sistema es el cilindro con las dos cámaras. Este sistema intercambia calor de dos modos. La cámara derecha cede o absorbe calor del foco a temperatura constante $T 0$ , de modo que la temperatura de esta cámara es siempre $T 0$ . La cámara de la izquierda intercambia calor con el sistema del que se quiere medir la temperatura. Es decir, ninguna de las dos cámaras es adiabática. Los procesos en la cámara de la derecha son isotermos, mientras que los de la izquierda no mantienen ninguna magnitud termodinámica constante.

Para medir la temperatura de un sistema ponemos en contacto la cámara izquierda con él. El trasvase de calor que se produce hace que varíe el estado del gas en esta cámara, por lo que se altera el valor de la presión. Entonces, el pistón se desplaza, con lo cual cambia el volumen de los dos gases. El equilibrio se recupera cuando la presión a ambos lados del pistón sea la misma. Los dos gases tendrán en general temperaturas distintas pues el pistón es adiabático y no permite el paso de calor.

Cuando las temperaturas son iguales en ambas cámaras el pistón está en el centro del cilindro y el volumen ocupado por los dos gases es el mismo

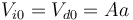
$V_{i0}=V_{d0}=Aa\,$

Como la temperatura de los dos gases en este caso es $T 0$ y la presión es $p 0$ , el número de moles es el mismo en las dos cámaras

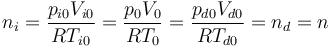
$\displaystyle n_i=\frac{p_{i0}V_{i0}}{RT_{i0}}=\frac{p_{0}V_{0}}{RT_{0}}=\frac{p_{d0}V_{d0}}{RT_{d0}}=n_d=n$

Si el pistón se desplaza hacia la derecha, el volumen de la cámara izquierda aumenta y el de la derecha disminuye

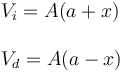
$\begin{array}{l} V_i=A(a+x)\\ \\ V_d=A(a-x) \end{array}$

Cuando el pistón se desplaza hacia la izquierda los valores de $x$ son negativos, con lo que estas expresiones también dan el valor correcto del volumen ocupado por cada gas.

Al poner en contacto el gas de la izquierda con el sistema a temperatura $T$ el nuevo equilibrio se alcanza cuando las presiones en los dos gases son iguales. En ese instante

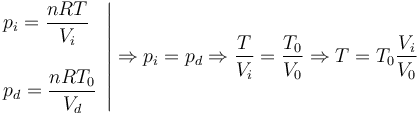
$\left. \begin{array}{l} \displaystyle p_i=\frac{nRT}{V_i}\\ \\ \displaystyle p_d=\frac{nRT_0}{V_d} \end{array} \right| \Rightarrow p_i=p_d\Rightarrow \displaystyle \frac{T}{V_i}=\frac{T_0}{V_0} \Rightarrow \displaystyle T=T_0\frac{V_i}{V_0}$

Usando las expresiones que nos dan los volúmenes en función de $x$ , teniendo en cuenta que el área $A$ aparece en el numerador y el denominador obtenemos

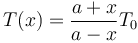
$\displaystyle T(x) = \frac{a+x}{a-x}T_0$

Está función no es lineal, pues su gráfica no corresponde a una línea recta.

Para examinar los límites propuestos en el enunciado despejamos $x$ en función de $T$

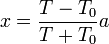
$\displaystyle x=\frac{T-T_0}{T+T_0}a$

Cuando 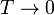$T\to 0$ obtenemos 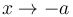$x\to -a$ . Si el sistema exterior está muy frío el pistón tiende a situarse en el extremo izquierdo. En el otro límite, si 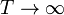$T\to\infty$ se tiene 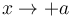$x\to +a$ . Si el sistema está muy caliente el pistón se desplaza hacia la derecha.

La figura muestra como depende la temperatura medida con la posición del émbolo. Pueden apreciarse los dos límites que hemos calculado.

3 Energía interna, calor y trabajo

Examinamos ahora los trasvases de calor, trabajo y variación de energía interna en el proceso termodinámico en cuestión. Suponemos que en el estado inicial la temperatura de ambos gases es $T 0$ , por lo que los volúmenes son iguales. El proceso es cuasiestático, esto es, los gases de las dos cámaras están siempre en equilibrio, es decir, con la misma presión a la izquierda y a la derecha (pero que cambia al calentarse el gas). Como el gas de la derecha está siempre a la temperatura $T 0$ el proceso en él es isotermo. Analizamos primero este pues es el más sencillo

3.1 Gas en la cámara derecha

Al ser iguales las temperaturas inicial y final, la energía interna del gas no cambia (es un gas ideal)

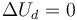
$\Delta U_d = 0\,$

Podemos calcular el trabajo que realiza el pistón sobre el gas pues el proceso es isotermo

$\displaystyle W_d=-\int_{V_0}^{V_d}p_d\mathrm{V_d}=-nRT_0\int_{V_0}^{V_d}\frac{\mathrm{d}V_d}{V_d}= -nRT_0\ln\frac{V_d}{V_0}= -nRT_0\ln\left(\frac{a-x}{a}\right)$

Con ayuda de la ecuación de los gases ideales podemos escribir esto sin usar el número de moles

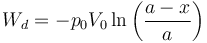
$W_d = -p_0V_0\ln\left(\frac{a-x}{a}\right)$

El Primer Principio de la Termodinámica nos dice que $Δ U = Q + W$ . Como $Δ U = 0$ nos queda

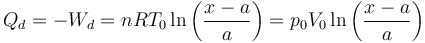
$Q_d = -W_d = nRT_0\ln\left(\frac{x-a}{a}\right)=p_0V_0\ln\left(\frac{x-a}{a}\right)$

El volumen que ocupa el gas en esta cámara es

$V_d = A(a-x) = V_0\frac{a-x}{a}$

y por tanto la presión en el equilibrio vale, por la ley de Boyle,

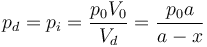
$p_d = p_i = \frac{p_0V_0}{V_d}=\frac{p_0a}{a-x}$

3.2 Gas en la cámara izquierda

Al ser un gas ideal la variación de energía interna depende únicamente de la temperatura. Entonces

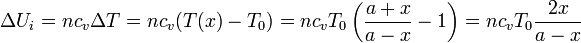
$\Delta U_i=nc_v\Delta T=nc_v(T(x)-T_0) = nc_vT_0\left(\frac{a+x}{a-x}-1\right)=nc_vT_0\frac{2x}{a-x}$

o, empleando la ley de los gases ideales, y la expresión para la capacidad calorífica a volumen constante

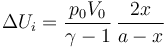
$\Delta U_i = \frac{p_0V_0}{\gamma-1}\,\frac{2x}{a-x}$

El trabajo es más difícil de calcular pues en este caso ninguna magnitud se mantiene constante. Podemos calcularlo si observamos que la presión en los dos gases es siempre la misma y que lo que aumenta el volumen de un lado es igual a lo que disminuye el volumen del otro.

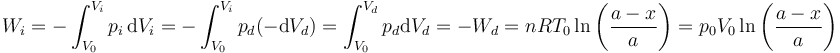
$W_i = -\int_{V_0}^{V_i}p_i\,\mathrm{d}V_i=-\int_{V_0}^{V_i}p_d(-\mathrm{d}V_d)=\int_{V_0}^{V_d}p_d\mathrm{d}V_d=-W_d= nRT_0\ln\left(\frac{a-x}{a}\right) = p_0V_0\ln\left(\frac{a-x}{a}\right)$

Este resultado también puede obtenerse si nos damos cuenta de que el trabajo sobre el sistema total es nulo, pues el volumen total del cilindro no cambia. Entonces, el trabajo que el gas de la izquierda realiza sobre el de la derecha debe ser igual al que el gas de la derecha realiza sobre el de la izquierda, cambiado de signo.

El calor que absorbe el gas de la izquierda lo obtenemos de la aplicación del Primer Principio

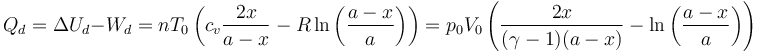
$Q_d=\Delta U_d-W_d = nT_0\left(c_v\frac{2x}{a-x}-R\ln\left(\frac{a-x}{a}\right)\right) = p_0V_0\left(\frac{2x}{(\gamma-1)(a-x)}-\ln\left(\frac{a-x}{a}\right)\right)$

El volumen final de esta cámara es

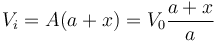
$V_i = A(a+x) = V_0\frac{a+x}{a}$

mientras que su presión final es la misma de la cámara de la derecha

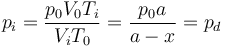
$p_i = \frac{p_0V_0T_i}{V_iT_0}=\frac{p_0a}{a-x}=p_d$

3.3 Tubo completo

La variación de energía interna es la suma de la variación en cada gas

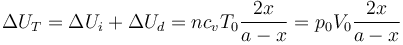
$\Delta U_T=\Delta U_i+\Delta U_d = nc_vT_0\frac{2x}{a-x}=p_0V_0 \frac{2x}{a-x}$

Como el volumen total del cilindro no cambia, el trabajo total es cero

$W_T=0\,$

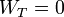
El calor total transferido lo obtenemos aplicando el Primer Principio

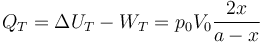
$Q_T = \Delta U_T-W_T=p_0V_0 \frac{2x}{a-x}$

La imagen muestra donde se realizan los trabajos y se producen las transferencias de calor en el sistema

4 Cálculo numérico de la temperatura

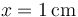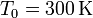De los datos del enunciado se deduce $a =10\,\mathrm{cm}$ y $x =1\,\mathrm{cm}$ . Si $T_0 = 300\,\mathrm{K}$ tenemos

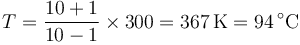
$T = \frac{10+1}{10-1}\times 300=367\,\mathrm{K}=94\,^\circ\mathrm{C}$

La presión en el equilibrio es

$p_d = p_i = \frac{p_0a}{a-x}= 111\,\mathrm{kPa}$

5 Cálculo numérico de calores, trabajos y variaciones de energía interna

Al ser aire el gas puede considerarse diatómico, es decir, $γ = 1.4$ . El volumen inicial es 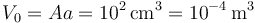$V_0=Aa=10^2\,\mathrm{cm}^3=10^{-4}\,\mathrm{m}^3$ . La presión inicial es 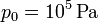$p_0=10^5\,\mathrm{Pa}$ . Con estos datos podemos calcular los valores numéricos pedidos.

5.1 Gas en la cámara derecha

$\begin{array}{l} \Delta U_d = 0\\ \\ \displaystyle W_d = -nRT_0\ln\left(\frac{a-x}{a}\right)=-p_0V_0\ln\left(\frac{a-x}{a}\right)=+1.05\,\mathrm{J}\\ \\ Q_d = -W_d = -1.05\,\mathrm{J} \end{array}$

5.2 Gas en la cámara izquierda

$\begin{array}{l} \displaystyle \Delta U_i = \frac{p_0V_0}{\gamma-1}\,\frac{2x}{(a-x)} =5.55\,\mathrm{J}\\ \\ \displaystyle W_i = nRT_0\ln\left(\frac{a-x}{a}\right)=-W_d =-1.05\,\mathrm{J}\\ \\ Q_i = \Delta U_i-W_i = 6.61\,\mathrm{J} \end{array}$

5.3 Tubo completo

$\begin{array}{l} \displaystyle \Delta U_T = \Delta U_i+\Delta U_d =5.55\,\mathrm{J}\\ \\ \displaystyle W_T = 0\\ \\ Q_T = \Delta U_T-W_T = 5.55\,\mathrm{J} \end{array}$

Termómetro de gas

De Laplace

Contenido

1 Enunciado

2 Escala de temperaturas

3 Energía interna, calor y trabajo

3.1 Gas en la cámara derecha

3.2 Gas en la cámara izquierda

3.3 Tubo completo

4 Cálculo numérico de la temperatura

5 Cálculo numérico de calores, trabajos y variaciones de energía interna

5.1 Gas en la cámara derecha

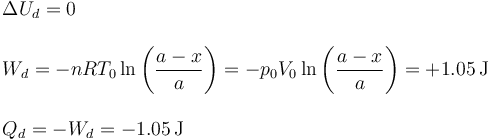
5.2 Gas en la cámara izquierda

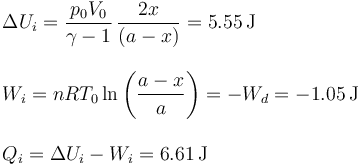
5.3 Tubo completo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES