MR 09 Fuerzas generalizadas
De Laplace
Fuerzas generalizadas
Al definir las coordenadas generalizados ampliamos el concepto de coordenada cartesiana para incluir cualquier magnitud que pueda usarse para caracterizar el estado de un sistema. En este apartado vamos a hacer un proceso similar para ampliar el concepto de fuerza al de fuerza generalizada. Veremos que a cada coordenada generalizada q se le puede asignar una magnitud escalar: su fuerza generalizada Qq. Esta fuerza generalizada recoge todas las contribuciones de las fuerzas y momentos del sistema que realicen un trabajo virtual cuando la coordenada generalizada sufre un desplazamiento virtual δq.
Consideremos un sistema holónomo con n grados de libertad: {qk}. Un desplazamiento virtual genérico se expresa {δqk}. Los desplazamientos virtuales de cualquier punto del sistema y las rotaciones virtuales se pueden expresar como
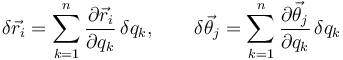
Sustituimos estas expresiones en el enunciado de del P.T.V. para un sistema de partículas y sólidos rígidos
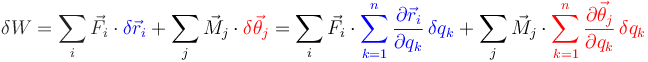
Usando la propiedad distributiva de la suma los sumatorios pueden intercambiarse
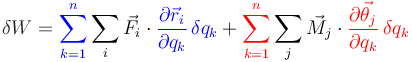
Y ahora sacamos factor común
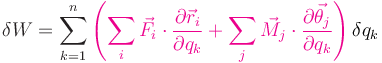
La expresión entre paréntesis es la fuerza generalizada Qk correspondiente a la coordenada generalizada qk
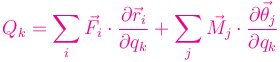
Vemos que recibe contribuciones de todas las fuerzas y momentos que realizan trabajo cuando la coordenada qk varía en δqk.
El P.T.V. puede expresarse como
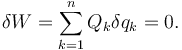
Se dice que un sistema es independiente si el número de coordenadas generalizadas y el número de grados de libertad es el mismo, es decir, todas las coordenadas generalizadas son independientes entre sí. Para que esto ocurra todas las ligaduras deben ser holónomas, aunque puede ocurrir que el sistema sea holónomo pero no independiente.
Para un sistema independiente, las qk pueden variar una cada vez sin afectar a las otras coordenadas. Entonces, para que se verifique el P.T.V. expresado en la forma anterior debe ocurrir que cada una de las fuerzas generalizadas sea cero, es decir
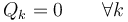
Esto proporciona n ecuaciones para las {qk}, con lo que el problema tiene solución.
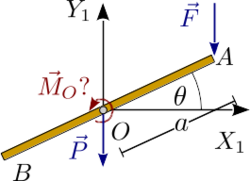
Vamos a analizar el ejemplo anterior usando fuerzas generalizadas. El problema tiene un grado de libertad y una coordenada generalizada {θ}. La fuerza generalizada es
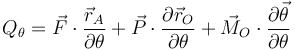
Usando las expresiones de 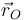 y
y 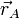 , y sabiendo que
, y sabiendo que 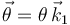 tenemos
tenemos
Qθ = − aFcosθ + MO
Como sólo hay un grado de libertad la condición de equilibrio es
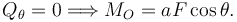
Por tanto, recuperamos el resultado obtenido antes.