Ley de Faraday (GIOI)
De Laplace
Contenido |
1 Evidencias experimentales
Los experimentos de Ørsted en 1820 pusieron de manifiesto que una corriente eléctrica produce un campo magnético, del mismo tipo que el causado por los imanes. El principio de reciprocidad, común a muchas áreas de la física, sugería que un campo magnético causa una corriente eléctrica. Sin embargo, durante 12 años los experimentos dieron resultados negativos. La simple presencia de un campo magnético no produce corriente alguna.
En 1831 Michael Faraday realizó importantes descubrimientos que probaban que efectivamente un campo magnético puede producir una corriente eléctrica, pero siempre que algo estuviera variando en el tiempo. Así descubrió:
- Si se mueve un imán en las proximidades de una espira, aparece una corriente en ésta, circulando la corriente en un sentido cuando el imán se acerca y en el opuesto cuando se aleja.
- El mismo resultado se obtiene si se deja el imán quieto y lo que se mueve es la espira.

- En lugar de un imán pueden usarse dos bobinas y se obtiene el mismo resultado. De nuevo, es indiferente cuál de las dos se mueva con tal de que haya un movimiento relativo.
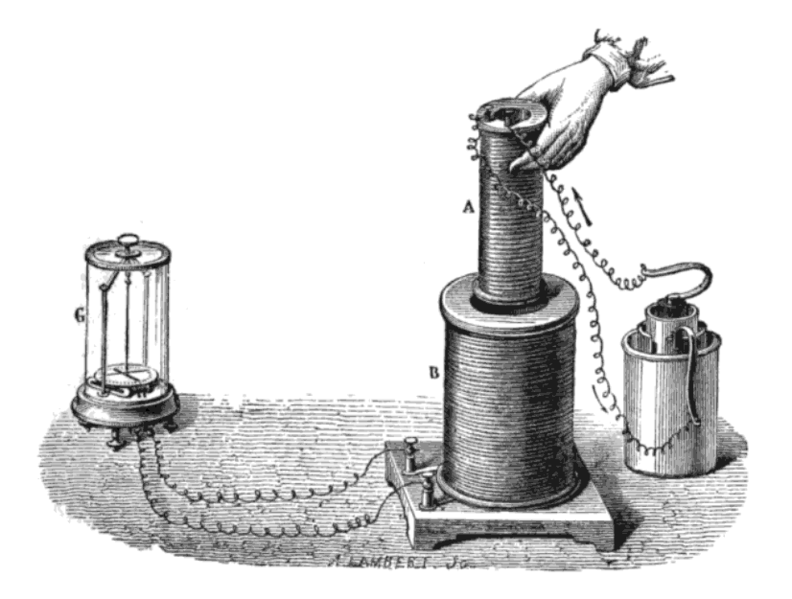
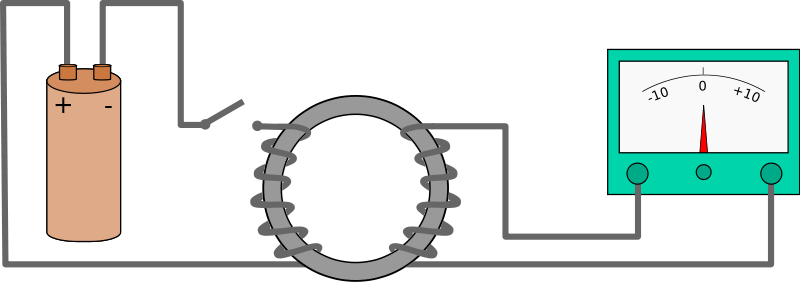
- No es imprescindible que haya movimiento. Faraday mostró que si arrollan dos bobinas alrededor de un núcleo de hierro, si por una de ellas (el “primario”) circula una corriente continua, en la otra (el “secundario”) no hay corriente alguna. Sin embargo, justo tras el cierre del interruptor, cuando la corriente del primario cambia en el tiempo, se induce una corriente en el secundario. Asimismo, tras la apertura del interruptor también aparece una corriente en el secundario, pero de sentido contrario a la anterior.
2 Enunciado de la ley de Faraday
2.1 General
Los resultados anteriores se pueden resumir todos en una sola forma matemática, conocida como ley de Faraday:
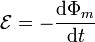
donde
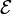
- es una fuerza electromotriz, adicional a otras que pudiera haber
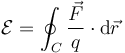
- siendo C una curva cerrada, que normalmente coincide con un circuito material (una malla de un circuito, por ejemplo), pero también puede ser una simple curva imaginaria. A esta f.e.m. se la denomina f.e.m. inducida.
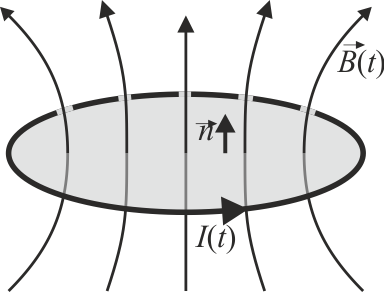
- Φm
- es el flujo magnético
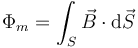
- siendo S una superficie apoyada en la curva C y orientada según la regla de la mano derecha respecto a esta. A la hora de aplicar la regla de la mano derecha es importante que se asigno el mismo sentido de recorrido a la hora de calcular la f.e.m y el flujo magnético.
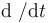
- es la derivada respecto al tiempo del flujo anterior. En el caso estacionario (corriente continua) la derivada es nula y no hay f.e.m. inducida.
- −
- El signo negativo es crucial en la ley de Faraday ya que nos indica el sentido de la corriente inducida. Las consecuencias de este signo se expresan en la ley de Lenz, que se comenta más adelante.
Una aplicación sencilla de la ley de Faraday sería el caso de una espira que penetra en un campo magnético uniforme.
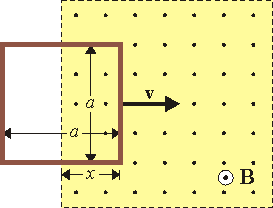
Considerando un sentido antihorario de recorrido de la espira, el vector a normal a una superficie apoyada en ella apunta hacia nosotros. El flujo magnético es igual al valor del campo por el área donde se halla, que no es toda la de la espira, sino solo la de la región ocupada por el campo.
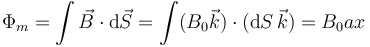
La fuerza electromotriz inducida por este flujo variable vale
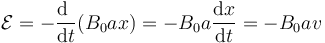
Si la espira tiene resistencia eléctrica R, la corriente que circula por ella es

En el caso de que la espira esté penetrando en el campo (v > 0), la corriente inducida es negativa, es decir, va en sentido horario (el opuesto al supuesto). Si está saliendo, es positiva, esto es, antihoraria (el mismo que el supuesto).
2.2 Caso de una espira móvil
A la hora de interpretar la ley de Faraday podemos plantearnos si es una consecuencia de otras leyes que conocemos. ¿Cuál es el origen de la f.e.m. inducida?
En el caso de una espira que se mueve en el seno de un campo magnético sí podemos hallar esta explicación. Consideremos en primer lugar el caso de una barra conductora que se mueve con velocidad 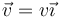 en el interior de un campo uniforme
en el interior de un campo uniforme 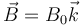 .
.
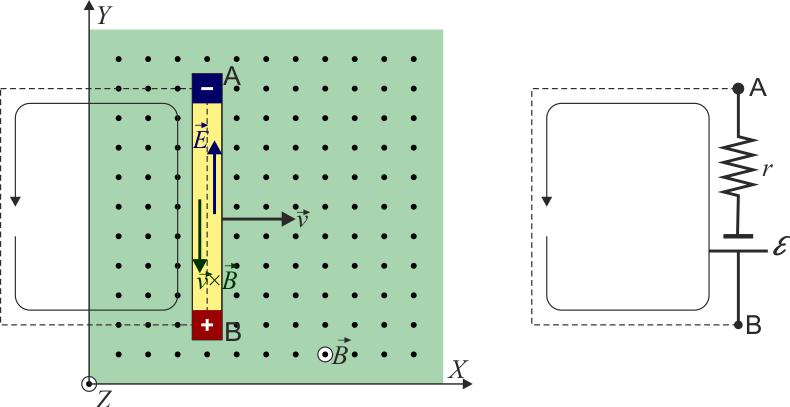
Sobre cada carga aparece una fuerza magnética
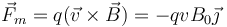
Esto quiere decir que sobre las cargas positivas aparece una fuerza hacia el extremo inferior de la barra y sobre las negativas una hacia el superior. El campo magnético provoca una separación de cargas y funciona como un campo efectivo 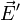 . La separación de cargas no es ilimitada. Una vez que las cargas se acumulan en los extremos se crea un campo eléctrico que se opone a la fuerza magnética. La separación se detiene cuando la fuerza sobre cada carga se anula
. La separación de cargas no es ilimitada. Una vez que las cargas se acumulan en los extremos se crea un campo eléctrico que se opone a la fuerza magnética. La separación se detiene cuando la fuerza sobre cada carga se anula
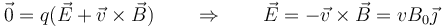
Este campo eléctrico dentro de la barra lleva asociada una diferencia de potencial entre el extremo superior y el inferior
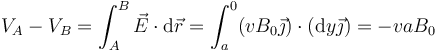
Lo que estamos describiendo no es otra cosa que un generador en circuito abierto. Los extremos de la barra funcionan como los polos de un generador (el positivo abajo, el negativo arriba).

Resulta una cantidad negativa porque recorremos la barra del polo positivo al negativo. No hay corriente circulando por la barra ya que la fuerza magnética y la eléctrica se anulan mutuamente.
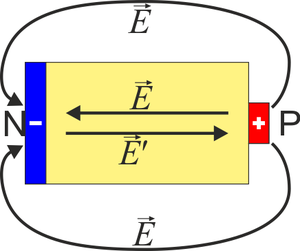
Supongamos ahora que la barra se cierra por otras tres, formando una espira cuadrada, estando uno de los lados en el exterior del campo magnético.
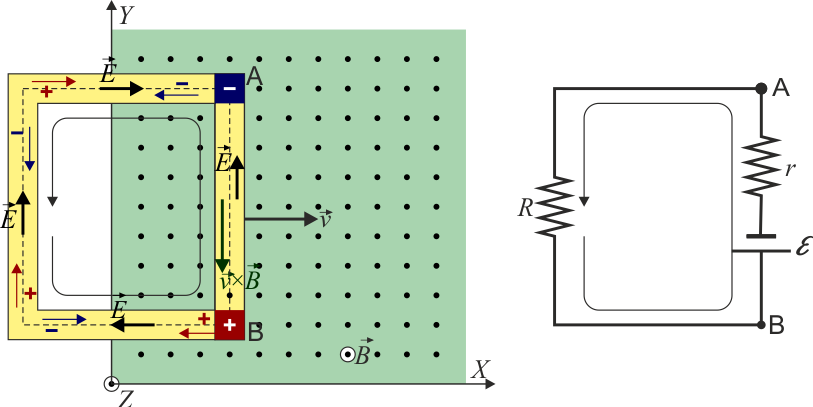
En este caso el campo eléctrico es capaz de reunir las cargas, moviéndolas por el exterior del campo magnético. Se produce entonces una corriente en la espira y tenemos un circuito cerrado. La barra que está dentro del campo magnético funciona como generador, con una resistencia interna igual a la resistencia óhmica de la barra. El resto de la espira funciona como resistencia externa. La corriente que circula por la espira, considerada en sentido antihorario es
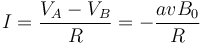
El mismo razonamiento se puede extender a otras espiras de formas arbitrarias y movimientos más complicados. En el caso del movimiento de una espira en un campo magnético estacionario, la fuerza electromotriz se debe a la fuerza magnética sobre las cargas en movimiento. Puede demostrarse que
2.3 Caso de una espira estacionaria
Supongamos ahora el caso de que tengamos una espira quieta y un imán en movimiento, que de las experiencias de Faraday sabemos que es equivalente al caso inverso. Si ahora nos preguntamos de nuevo quién mueve las cargas llegamos a que
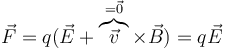
es decir, que en este caso, es la fuerza eléctrica la que mueve las cargas a lo largo de la espira. Pero, ¿cómo puede un campo eléctrico mover a las cargas en un circuito cerrado? ¿No equivale eso a que las cargas den vueltas cerradas yendo siempre “cuesta abajo” (o “cuesta arriba”, si son negativas), lo cual es imposible?

La respuesta es que este campo eléctrico no es un campo electrostático. No está causado por cargas eléctricas, no va de las cargas positivas a las negativas, ni de mayor a menor potencial.
Se trata de un campo eléctrico inducido por la variación del campo magnético, cumpliéndose la relación
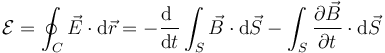
Si el campo magnético es constante o no existe, como ocurre en electrostática, el segundo miembro se anula y recuperamos el resultado de que un campo electrostático no puede conseguir que las cargas recorran un circuito cerrado.
Tenemos entonces que hay dos posibles fuentes de campo eléctrico:
- Las cargas eléctricas: las cargas positivas son manantiales de campo eléctrico, mientras que las negativas son sumideros.
- Los campos magnéticos variables en el tiempo: este campo eléctrico no tiene manantiales ni sumideros sino que puede tener líneas de campo cerradas alrededor del campo magnético.
3 Consecuencias
3.1 Ley de Lenz
El signo que aparece en la ley de Faraday tiene consecuencias muy importantes.
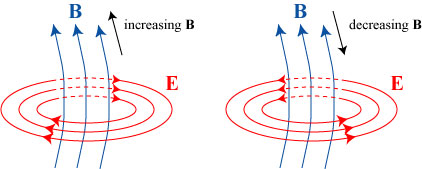
Consideremos el caso de un imán que se acerca por su polo norte a una espira conductora. A través de la espira, el flujo magnético está aumentando. De acuerdo con la ley de Faraday, la f.e.m. inducida es negativa, y la corriente que se induce en la espira es tal que el campo que ella misma produce se opone al campo aplicado. La cara norte de la espira está en la parte inferior y la cara sur en la superior. Esto implica que, además, la espira es repelida por el imán.
Parecería entonces que el campo inducido se opone al campo inductor, pero no es así. Supongamos ahora que el imán se está alejando de la espira (pero ofreciendo también su polo norte). En este caso el flujo magnético está disminuyendo y la corriente inducida es tal que el campo magnético inducido refuerza al inductor.
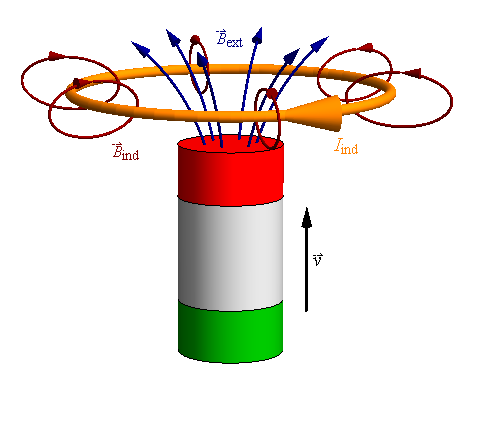

Vemos entonces que el sentido del campo inducido no depende solo del sentido del campo aplicado, sino de la variación de éste. Esto se expresa mediante la ley de Lenz:
- El sentido de la corriente inducida es tal que el campo que produce se opone a la variación del flujo del campo aplicado.
Si el campo está disminuyendo, tiende a aumentarlo; si está aumentando tiende a disminuirlo. Vemos así que los sistemas poseen una inercia, y tienden a permanecer en el estado en que estaban.
La ley de Lenz es la responsable, entre otros fenómenos, de las chispas que saltan al desenchufar un aparato, ya que el sistema tiende a mantener la corriente incluso aunque se abra el circuito, por lo que aparece una corriente inducida que circula brevemente por el aire, cerrando el circuito.
Esta ley es muy útil como regla para intuir el sentido de la corriente inducida, sin necesidad de hacer cálculos. Por ejemplo, en el caso de la espira cuadrada que penetra en el campo magnético, descrito anteriormente, la corriente inducida debe ser tal que su campo propio se oponga al existente y por tanto, debe ir hacia adentro del plano. La cara que vemos de la espira es una cara sur y la corriente en ella debe ser en sentido horario.
La ley de Lenz también se aplica a casos que no hay movimiento, como el de las dos bobinas ilustrado arriba. Al cerrar el interruptor el flujo magnético debido al primario aumenta, por lo que la corriente inducida en el secundario debe hacerlo disminuir. Al abrir el interruptor el flujo magnético del primario disminuye, por lo que la corriente inducida debe hacerlo aumentar.
3.2 Propiedades generales del campo eléctrico
La existencia de un campo eléctrico inducido por los campos magnéticos variable obliga a revisar muchas propiedades del campo eléctrico que son válidas solo en situaciones estáticas. Cuando se considera el caso de un campo eléctrico general, suma del debido a las cargas y a los campos magnéticos, hay que tener en cuenta las siguientes propiedades:
- El campo eléctrico es capaz de mover cargas a lo largo de una curva cerrada
- En electrostática el campo eléctrico solo puede mover cargas positivos de puntos de mayor a menor potencial, pero no en sentido inverso. Un campo inducido sí puede hacerlo y mantener una corriente en una curva cerrada.
- La circulación del campo eléctrico en una curva cerrada puede no ser nula
- es consecuencia de lo anterior, que se deduce de la ley de Faraday
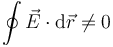
- Este permite, entre otras consecuencias, que el campo eléctrico tenga líneas de campo cerradas.
- El voltaje entre dos puntos depende del camino de integración
- Es consecuencia de lo anterior

- Esto implica que dos voltímetros conectados a los mismos puntos pueden dar lecturas diferentes. Esto no es lo habitual, pero cuando hay campos magnéticos variables en el sistema es necesario tener cuidado.
- No existe el potencial eléctrico
- La existencia del potencial eléctrico se deduce de que el campo eléctrico es conservativo. Esto es cierto en electrostática, pero no en general. Por tanto, no puede definirse una función
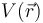 de la cual derive el campo eléctrico. Por la misma razón, en general no puede hablarse de diferencia de potencial, sino que es más correcto referirse al voltaje.
de la cual derive el campo eléctrico. Por la misma razón, en general no puede hablarse de diferencia de potencial, sino que es más correcto referirse al voltaje.
4 Aplicaciones
El número de aplicaciones de la ley de Faraday es infinito. Prácticamente toda la tecnología eléctrica se basa en ella, ya que generadores, transformadores y motores eléctricos se basan en ella. Aquí indicamos algunas de las aplicaciones más directas.
4.1 Generador
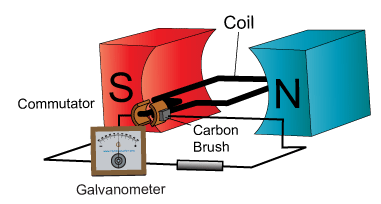
Al principio de este artículo se describe un generador de corriente continua elemental, consistente en una espira que penetra en un campo magnético. Este generador carece de utilidad práctica.
Mucho más importante es el alternador presente en la mayoría de las centrales eléctricas. En un alternador una turbina (movida por agua o vapor, por ejemplo) hace girar un imán (el rotor) estando rodeado por una serie de bobinas (el estator) en las que se induce una corriente eléctrica. Como el campo magnético se encuentra en rotación con velocidad angular ω el resultado es una corriente alterna de frecuencia angular ω. Cuando se usan 3 o 6 bobinas el resultado son tres corrientes alternas desfasadas un tercio de periodo, que es lo que se conoce como corriente alterna trifásica.
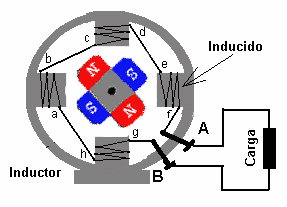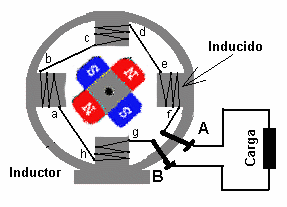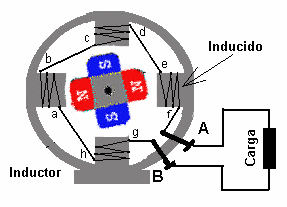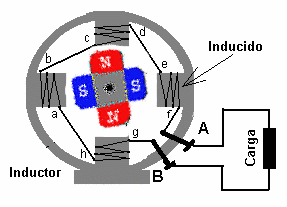
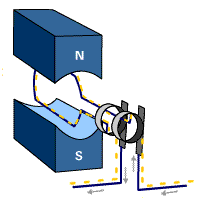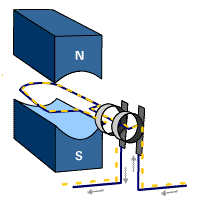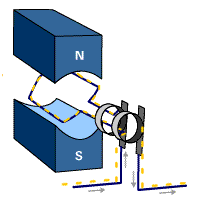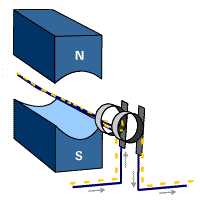
También puede construirse un generador mediante el sistema inverso de hacer girar una espira en un campo magnético estacionario. Empleando conexiones adecuadas puede conseguirse además que la corriente vaya siempre en el mismo sentido, lo que permite construir un generador de corriente continua.
4.2 Motor eléctrico
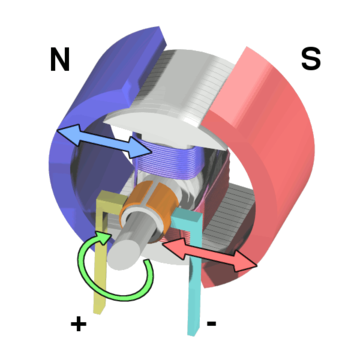
Relacionado con el generador está el motor eléctrico, en el cual lo que se hace es girar un electroimán (el rotor) en el interior del campo magnético creado por otros electroimanes (el estator). Haciendo que por el rotor circule una corriente alterna se puede conseguir una rotación continuada.
4.3 Transformador
Al estudiar los efectos de inducción de una bobina (primario) sobre otra (secundario) se obtiene que en el caso ideal, el voltaje que resulta en el secundario es proporcional al voltaje del primario. De esta manera se puede elevar o reducir el voltaje a voluntad. El dispositivo formado por estas dos bobinas alrededor de un núcleo es un transformador
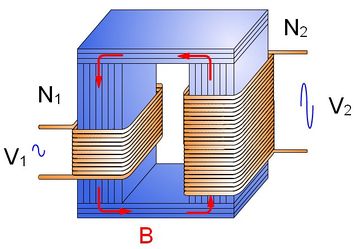
Los transformadores son esenciales en la transmisión de la energía eléctrica, porque al mismo tiempo que aumentan el voltaje, reducen la intensidad de corriente. De esta forma se minimizan las pérdidas por efecto Joule en la distribución de energía eléctrica.
4.4 Freno magnético
Otra aplicación directa de la ley de Faraday es su uso en frenos magnéticos. Estos no se basan, como podría pensarse, en la atracción magnética sobre una pieza de hierro o acero.



No es así, consiste en un electroimán que rodea a un disco metálico, unido rígidamente a la rueda que se desea frenar. Cuando se aprieta el pedal, se hace circular corriente por el electroimán, creando un campo magnético sobre el disco. Por la ley de Faraday se inducen corrientes en el material conductor. Estas corrientes en el interior del material se denominan corrientes de Foucault (eddy currents en ingles). Al existir corrientes se disipa energía por fecto Joule. Esta energía procede de la energía cinética de la rueda, que por tanto se ve frenada.
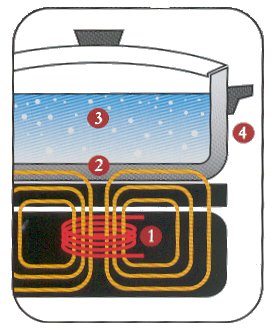
4.5 Cocinas de inducción
El mismo principio de los frenos magnéticos se plica si lo que queremos es producir calor. Una cocina de inducción consiste en un imán en espiral situado debajo de la placa vitrocerámica, que produce un campo magnético alterno (que varía como el coseno de ωt). Al colocar sobre la cocina un recipiente metálico se inducen corrientes de Foucault en el propio recipiente y en el agua y alimentos que contiene. El calor liberado por estas corrientes es el que se emplea para cocinar los alimentos