Gradiente
De Laplace
Contenido |
1 Definición
De la definición de derivada direccional resulta que dado un campo escalar, continuo y derivable, para cada punto del espacio existen infinitas derivadas direccionales, una por cada dirección. Resulta además que el concepto de derivada direccional depende tanto del campo escalar como de la dirección elegida.
¿Existe alguna cantidad, independiente de la dirección, que permita calcular las derivadas direccionales, sin necesidad de hallar infinitas cantidades para cada punto.
La respuesta la da el gradiente: Para un campo escalar  y un punto P, el gradiente
y un punto P, el gradiente 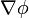 del campo en dicho punto es el único vector, dependiente exclusivamente del campo, tal que para cualquier dirección
del campo en dicho punto es el único vector, dependiente exclusivamente del campo, tal que para cualquier dirección  , la derivada direccional de
, la derivada direccional de  en P viene dada por el producto escalar
en P viene dada por el producto escalar
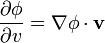
Equivalentemente, el gradiente puede definirse como el único vector tal que para cualquier desplazamiento diferencial \mathrm{d}\mathbf{r}, el incremento diferencial de  vale
vale

No demostraremos que esta definición implica que dicho vector existe y además es único.
2 Propiedades
A partir de la definición, pueden demostrarse varias propiedades generales que no requieren el uso de ningún sistema de coordenadas:
- El gradiente es ortogonal a las superficies equiescalares
- Sea un punto
 en el que está definido el campo
en el que está definido el campo  y consideremos una dirección tangente a una superficie equiescalar. La derivada direccional en dicha dirección es nula pues el valor del campo no cambia si nos movemos sobre una superficie equiescalar
y consideremos una dirección tangente a una superficie equiescalar. La derivada direccional en dicha dirección es nula pues el valor del campo no cambia si nos movemos sobre una superficie equiescalar
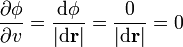
- Pero, por otro lado,
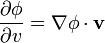
- Por tanto
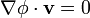

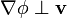
- para todas las direcciones tangentes a la superficie equiescalar. Si el gradiente es perpendicular a todas las direcciones tangentes a la superficie equiescalar, se deduce que es un vector perpendicular a la superficie equiescalar en dicho punto.
- De esta propiedad se deduce que el plano tangente a una superficie equiescalar en un punto
 tiene la ecuación vectorial
tiene la ecuación vectorial
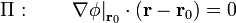
- El gradiente apunta en la dirección en que la derivada direccional es máxima
- Consideremos un campo escalar en un punto
 y evaluemos los posibles valores de las derivadas direccionales en dicho punto. De acuerdo con las definciones de gradiente y de producto escalar
y evaluemos los posibles valores de las derivadas direccionales en dicho punto. De acuerdo con las definciones de gradiente y de producto escalar
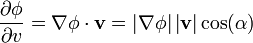
- siendo α el ángulo que forman el vector gradiente y el vector
 . Ahora bien, el módulo del gradiente será el que sea, pero en cualquier caso es independiente de la dirección de
. Ahora bien, el módulo del gradiente será el que sea, pero en cualquier caso es independiente de la dirección de  que tomemos. El módulo de
que tomemos. El módulo de  es la unidad. Por tanto los posibles valores de la derivada direccional, como función de la dirección, cumplen
es la unidad. Por tanto los posibles valores de la derivada direccional, como función de la dirección, cumplen
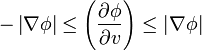
- alcanzándose el valor máximo cuando
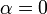 esto es, cuando la dirección de
esto es, cuando la dirección de  coincide con la del gradiente en ese punto.
coincide con la del gradiente en ese punto.
- Por tanto,
- la dirección del gradiente es aquella en que la derivada direccional es máxima.
- su sentido es aquél en que
 crece (ya que la derivada direccional es positiva).
crece (ya que la derivada direccional es positiva).
- su módulo es el valor de la derivada direccional máxima.
- El gradiente es nulo en los puntos críticos (máximos, mínimos y puntos de silla)
- Supongamos un campo escalar derivable que alcanza su valor máximo en un punto
 . En este punto, sea cual sea la dirección que tomemos, el valor de la función es máximo, por lo que la derivada direccional debe anularse (del mismo modo que la derivada de una función de una sola variable se anula en un máximo). Por tanto, para todo
. En este punto, sea cual sea la dirección que tomemos, el valor de la función es máximo, por lo que la derivada direccional debe anularse (del mismo modo que la derivada de una función de una sola variable se anula en un máximo). Por tanto, para todo  ,
,
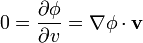
- y puesto que el único vector cuyo producto por cualquier otro es nulo es el vector nulo, se deduce que
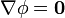 en un máximo
en un máximo- Por la misma razón
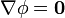 en un mínimo
en un mínimo- Esto es, el gradiente se anula en los extremos de la función (donde ésta sea derivable en todas direcciones). Inversamente, si el gradiente de un campo escalar se anula en un punto, podemos concluir que en dicho punto el campo posee un punto crítico, que puede ser:
- Un máximo
- Un mínimo
- Un punto de silla
- Para determinar de qué clase de punto crítico se trata, es preciso considerar las derivadas de orden superior. Si estas también se anulan, puede haber algún caso más, como que sea un punto de inflexión.





