Fuerzas ficticias (GIOI)
De Laplace
Contenido |
1 Introducción
Es común tanto en la vida diaria como en algunos libros de divulgación o de texto, el hablar de la “fuerza centrífuga'” como una fuerza real que mueve los objetos, empujándolos hacia afuera, responsable de que por ejemplo la Luna no se estrelle contra la Tierra. Incluso algún libro la identifica como la reacción a la fuerza centrípeta, que sería la acción.
Sin embargo, ¿quién ejerce la fuerza centrífuga? ¿Es eléctrica, gravitatoria o de qué tipo? ¿Si alguien ejerce una fuerza centrífuga sobre una partícula, ejercerá la partícula una fuerza centrífuga sobre ese alguien?
La respuesta es que nadie ejerce la fuerza centrífuga, porque la fuerza centrífuga no existe. Es una fuerza ficticia, un artificio matemático consecuencia de la generalización de las leyes de Newton a sistemas no inerciales.
Más adelante daremos la expresión matemática de esta fuerza ficticia, pero es fácil interpretarla con un ejemplo sencillo. Imaginemos un patinador montado en el interior de un vagón de tren, sin ningún tipo de rozamiento con el suelo.
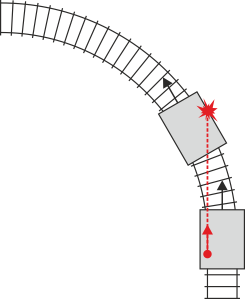
Cuando el tren toma una curva hacia la izquierda, el patinador, sobre el que no actúa ninguna fuerza, continúa en línea recta, con lo que finalmente es golpeado por la pared derecha del vagón. ¿Qué entiende el patinador (que solo ve el vagón y no el exterior)? Que de pronto ha actuado sobre él una fuerza hacia la derecha que ha terminado llevándolo hasta la pared. Pero esta fuerza es ficticia, es solo el resultado de emplear un sistema de referencia (el vagón) que está en rotación.
2 Sistema con aceleración lineal
Antes de analizar el caso de un sistema en rotación, consideraremos un caso más simple: el de un sistema de referencia que se traslada de forma acelerada respecto a uno inercial.
De nuevo, el ejemplo es el de un vagón de tren que se desplaza de manera acelerada por un camino ahora rectilíneo. Si del techo de este vagón cuelga un péndulo sabemos que el hilo se inclinará hacia atrás cuando el tren acelera y hacia adelante cuando frena. ¿Por qué lo hace? ¿Qué fuerza horizontal actúa sobre la masa para desviarlo de la vertical?
2.1 Interpretación por un observador inercial
Veamos cómo sería empleando las leyes de Newton en un sistema de referencia inercial, que sería el de un observador situado fuera del tren. Para este observador, la lenteja del péndulo se encuentra en reposo respecto al tren, es decir, se mueve aceleradamente respecto al observador. De acuerdo con la segunda ley de Newton esto implica que la masa no está en equilibrio, sino que debe haber una fuerza neta que actúa sobre ella. Las dos únicas fuerzas posibles son el peso y la tensión del hilo, por lo que
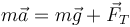
Separando en componentes
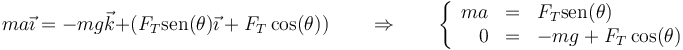
Si despejamos y dividimos nos queda, para el ángulo,
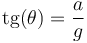
con lo cual, midiendo el ángulo, tenemos la aceleración, que podrá ser tanto positiva como negativa. Este es el principio de muchos acelerómetros.
Lo importante aquí es que (1) El péndulo no está en equilibrio, sino acelerado, (2) sobre la masa actúan dos fuerzas reales: peso y tensión y (3) la suma de las fuerzas no es cero.
Ahora bien, ¿cómo explica la inclinación un observador que va dentro del tren y por tanto no aprecia aceleración en la masa colgante?
2.2 Relación entre los sistemas de referencia
Para relacionar las medidas de los dos observadores debemos introducir dos sistemas de referencia:
- Uno inercial (usualmente llamado sistema laboratorio o sistema fijo) asociado al observador externo. Etiquetaremos este sistema como “1”. Su origen de coordenadas es el punto O1 y sus vectores de la base canónica son
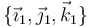 .
.
- Uno no inercial (denominado sistema móvil), que sería el del tren. Etiquetaremos este sistema como “0”. Su origen de coordenadas es el punto O0 y los vectores de su base canónica son
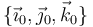 .
.
- La partícula en sí misma constituye un cuerpo adicional que etiquetaremos como 2. Aunque en el contexto de cinemática de la partícula esta etiqueta es superflua (ya que la identificamos a la vez como P y como “2”), la mantendremos ya que sí es útil al estudiar el movimiento de un sólido y de esta manera se evitan confusiones.
Dado que el sistema móvil describe un movimiento rectilíneo sin rotación, los vectores de la base móvil son los mismos que los de la base fija. Más adelante veremos qué ocurre cuando hay rotación.
La posición de una partícula que se mueve respecto a los dos sistemas verifica la relación entre posiciones relativas

Si derivamos aquí respecto al tiempo obtenemos una relación entre velocidades
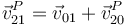
siendo 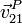 y
y 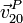 las velocidades de la partícula (“2”) respecto a los sistemas fijo (“1”) y móvil (“0”), respectivamente y
las velocidades de la partícula (“2”) respecto a los sistemas fijo (“1”) y móvil (“0”), respectivamente y  la velocidad instantánea con que se traslada el sistema móvil respecto al fijo.
la velocidad instantánea con que se traslada el sistema móvil respecto al fijo.
Derivando de nuevo obtenemos una relación entre aceleraciones

2.3 Fuerza ficticia de inercia
Desde el punto de vista cinemático no existe una diferencia esencial entre el sistema “1” y el “0”. Sus papeles podrían intercambiarse y las relaciones entre velocidades y aceleraciones seguirían siendo ciertas sin más que permutar los índices.
Sin embargo, desde el punto de vista dinámico existe una diferencia esencial. Por ser el sistema fijo uno inercial, en él se cumplen las leyes de Newton
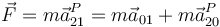
Esto quiere decir que si el observador móvil intenta aplicar las leyes de Newton en su sistema el producto de la masa por la aceleración no es igual a la fuerza aplicada, sino que
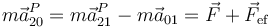
es decir, este observador percibe una fuerza efectiva adicional igual al producto de la masa por la aceleración relativa entre los dos sistemas, cambiada de signo.
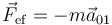
Esta es una fuerza ficticia. No hay ningún agente ejerciendo esta fuerza, sino que se trata de un artificio matemático que permite aplicar las leyes de Newton en este sistema de referencia.
Volviendo al sistema del péndulo en el vagón, para el observador móvil el péndulo se encuentra en equilibrio, por tanto, según él la suma de fuerzas debe ser nula. Para este observador, sobre la partícula actúan tres fuerzas: el peso, la tensión y la fuerza ficticia, cumpliéndose
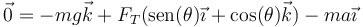
que lleva naturalmente al mismo resultado (solo hemos cambiado un término de miembro). Dando un paso más, el observador móvil puede interpretar el resultado como que la gravedad apunta en una dirección diferente
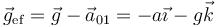
Esto es consecuencia de que la masa inercial y la gravitatoria sean idénticas y puedan extraerse la masa como factor común. En esta interpretación el péndulo está “vertical” pero respecto a la gravedad efectiva.
La visión de la fuerza ficticia como un cambio en la gravedad permite resolver esta cuestión: Si estamos montamos en un coche y sujetamos un globo de helio flotando y aceleramos el coche hacia adelante, ¿hacia dónde va el globo? La gravedad efectiva tiene ahora una componente hacia atrás. Por tanto el globo, que es menos pesado que el aire, se mueve hacia adelante, por el principio de Arquímedes.
Aún podemos dar un paso más y hacer la pregunta al revés: si la fuerza ficticia puede verse como una gravedad efectiva, ¿es posible interpretar la gravedad como una fuerza ficticia? ¿Es simplemente el resultado aparente de hacer observaciones en sistemas no inerciales? Esta pregunta entra de lleno en la Teoría de la Relatividad General. La respuesta es “sí, pero…”.
3 Sistema de referencia en rotación
Consideremos ahora el caso de que el observador móvil no se traslada, sino que está en un sistema giratorio. El ejemplo típico es la superficie de un tiovivo, pero también vale para la Tierra en su movimiento de rotación.
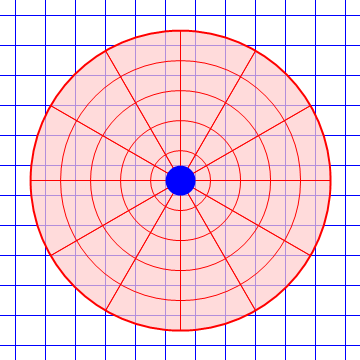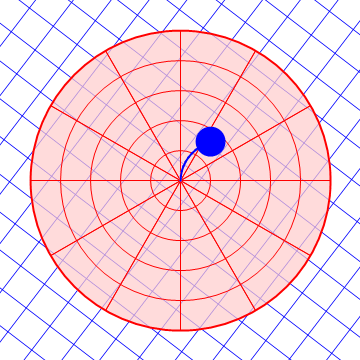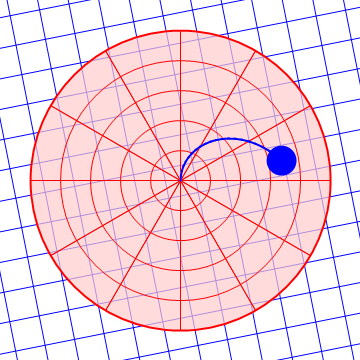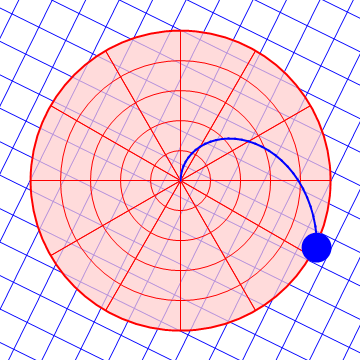
| Desde el suelo | Desde la plataforma |
|---|---|
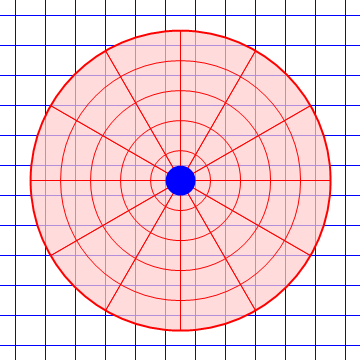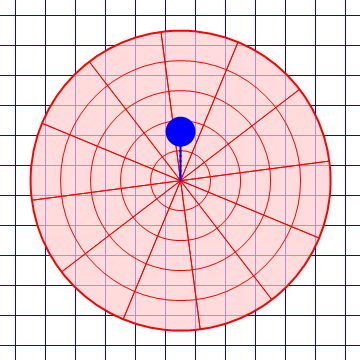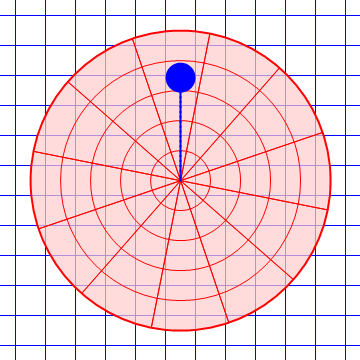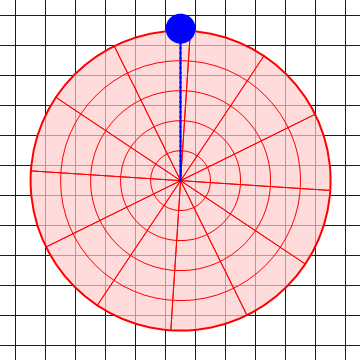
| 
|
Es claro que el observador móvil ve que los objetos se desvían lateralmente debido a la presencia de fuerzas adicionales.
En este caso podemos tomar el mismo origen de coordenadas, pero la orientación de los ejes va cambiando con el tiempo. Esto quiere decir que ahora el triedro móvil va a ser una función del tiempo y por tanto habrá que tenerlo en cuenta a la hora de derivar.
3.1 Fórmula de Poisson
Para una magnitud escalar (por ejemplo, la temperatura), que no depende de la base que se elija, los dos observadores estarán de acuerdo en su valor en cada instante y en cuánto vale su derivada respecto al tiempo
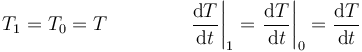
Supongamos ahora una magnitud vectorial (como puede ser la velocidad, o la fuerza aplicada). Esta magnitud tendrá una cierta descomposición en la base fija y otra en la móvil
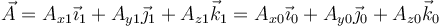
Hay que recordar que la magnitud vectorial es la misma, lo que cambian son sus componentes.
Cuando derivamos esta cantidad respecto al tiempo, tal como lo ve el observador inercial fijo, obtenemos que
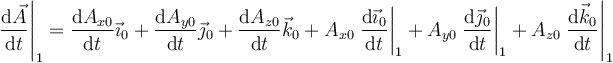
Los primeros tres sumandos no llevan el subíndice en la derivada porque al ser cantidades escalares los dos observadores están de acuerdo en su valor. La suma de estos tres términos es lo que el observador móvil interpreta como la derivada temporal de  (ya que para él los vectores de su base no se mueven)
(ya que para él los vectores de su base no se mueven)
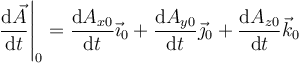
Ahora bien, ¿qué ocurre con los otros tres términos? Son los asociados a la rotación de los ejes. ¿Qué tipo de movimiento realiza el vector 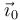 ? Es un vector de módulo constante, por lo que su derivada temporal será ortogonal a él mismo.
? Es un vector de módulo constante, por lo que su derivada temporal será ortogonal a él mismo.
En el caso de un tiovivo horizontal, lo que hace el vector 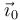 es describir circunferencias, por lo que se cumple la misma ecuación que para un movimiento circular
es describir circunferencias, por lo que se cumple la misma ecuación que para un movimiento circular
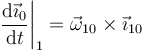
siendo  la velocidad angular con la que gira el sistema móvil respecto al fijo. Esta ecuación es general ya que el eje de giro no tiene por qué ser el eje Z. De la misma manera, los otros dos vectores de la base realizan la misma rotación
la velocidad angular con la que gira el sistema móvil respecto al fijo. Esta ecuación es general ya que el eje de giro no tiene por qué ser el eje Z. De la misma manera, los otros dos vectores de la base realizan la misma rotación

Esto nos permite relacionar las derivadas temporales vistas por uno y otro observador

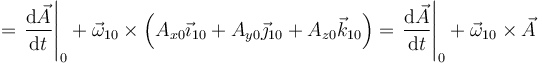
Llegamos finalmente a la conocida como fórmula de Poisson:
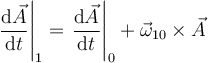
que nos relaciona la derivada temporal que mide el observador fijo con la que mide el observador móvil. Aquí  es cualquier magnitud vectorial.
es cualquier magnitud vectorial.
3.2 Teorema de Coriolis
Al tener el mismo origen de coordenadas, los dos observadores coinciden en el vector de posición de una partícula que se mueve respecto a ambos. Sin embargo discrepan en cuanto a la velocidad con la que se mueve.
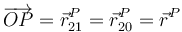
Cuando aplicamos la fórmula de Poisson al caso del vector de posición queda
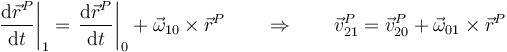
es decir, la velocidad con la que el observador fijo ve moverse la partícula es la suma de la que tiene en su traslación en el sistema móvil más la que tiene por la rotación de este sistema.
Si ahora volvemos a aplicar la fórmula de Poisson a las velocidades obtenemos la relación entre las aceleraciones.
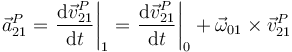
Sustituimos aquí la relación entre velocidades
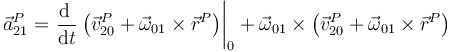
Desarrollamos la derivada respecto al tiempo y nos queda
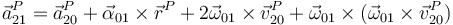
Este es el conocido como teorema de Coriolis.
El factor 2 del tercer sumando proviene de que hay un término procedente de la derivada de la posición y otro del producto vectorial.
Multiplicando por la masa y despejando llegamos a la fuerza aparente que mide el observador móvil
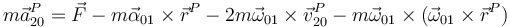
Como vemos, aparecen tres fuerzas ficticias adicionales que consideramos por separado.
3.2.1 Fuerza centrífuga
El término
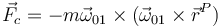
se conoce como “fuerza centrífuga”. Para ilustrar su efecto consideremos de nuevo la plataforma del tiovivo. La velocidad angular de esta plataforma es perpendicular a ella y un vector de posición es tangente a ella

con lo que, aplicando el doble producto vectorial, la fuerza centrífuga se reduce a

Es decir, se trata de una fuerza ficticia radial y hacia el exterior desde el eje del movimiento circular. Con ayuda de esta fuerza ficticia podemos explicar los movimientos de rotación uniformes como situaciones de equilibrio entre una fuerza radial hacia el interior (la fuerza gravitatoria en el caso orbital o una tensión en el péndulo cónico) conocida como fuerza centrípeta y una radial hacia el exterior que sería la fuerza centrífuga. Hay que insistir, no obstante en que se trata de la interpretación de un observador en rotación. En un sistema fijo la fuerza centrífuga no existe. Solo está la centrípeta, que provoca aceleración radial hacia adentro.
La fuerza centrífuga puede emplearse para calcular el ángulo que forma con la vertical un péndulo rotatorio
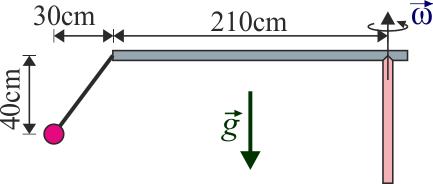
El péndulo se comporta como si estuviera “vertical” respecto a una gravedad dependiente de la posición como

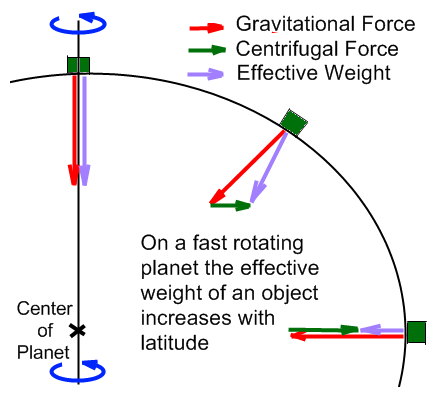
Llevando este mismo cálculo a la gravedad aparente en la superficie terrestre resulta que si suponemos ésta una esfera perfecta, la gravedad aparente (medible con plomadas y péndulos) no apunta en la dirección puramente radial, sino que se desvía por efecto de la aceleración centrífuga.
Este efecto depende de la latitud, ya que la aceleración centrífuga va siempre en la dirección horizontal y además depende de la distancia al eje de rotación, que es nula en los polos y máxima en el ecuador.
Si λ es la latitud medida desde el ecuador, podemos emplear coordenadas cilíndricas para escribir la gravedad aparente
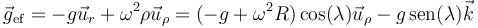
En módulo, esta gravedad aparente varía desde un valor máximo en los polos

a uno mínimo en el ecuador
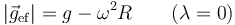
Dado que  , hay un 0.3% de variación entre los polos y el ecuador.
, hay un 0.3% de variación entre los polos y el ecuador.
La situación real es más compleja porque la Tierra no es esférica, sino achatada, justamente por los efectos centrífugos, siendo la variación por este efecto comprable a la desviación por la fuerza centrífuga.
3.2.2 Fuerza de Coriolis
El segundo de los términos que consideramos es el de la llamada fuerza de Coriolis, correspondiente a

Este término es no nulo sólo si 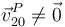 , es decir, requiere que la partícula se esté moviendo respecto al sistema en rotación.
, es decir, requiere que la partícula se esté moviendo respecto al sistema en rotación.
La fuerza de Coriolis es la fuerza ficticia que experimenta, por ejemplo, una piedra que es lanzada radialmente por un individuo situado en el eje de una plataforma en rotación. Atendiendo al desplazamiento horizontal, para un observador fijo externo la partícula describe una recta. Para el observador móvil (para el cual la partícula “se va quedando atrás”) existe una aceleración lateral que interpreta como que hay una fuerza actuando sobre la partícula.
Si nos restringimos al movimiento en el plano de una plataforma giratoria 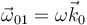 y queda
y queda

Esta fuerza es siempre ortogonal a la velocidad y, para este giro de la plataforma, siempre en el sentido hacia la derecha de la velocidad.
La fuerza de Coriolis es la responsable del sentido de giro de grandes masas de aire como los vientos alisios o los ciclones. No obstante, para que sus efectos sean apreciables en el movimiento de un fluido son necesarias grandes masas y extensiones. Por ello, no es responsable del sentido de giro de un tornado (que puede ir en los dos sentidos), ni mucho menos del giro del agua en el desagüe de una bañera.
En el caso de un ciclón el movimiento del aire se produce porque en su centro (el llamado ojo del huracán) existe una zona de muy bajas presiones, por lo que el aire acude desde el exterior en una dirección radial. Sin embargo, al converger el aire se ve desviado hacia la derecha (en el hemisferio norte), produciendo un giro antihorario del ciclón perfectamente observable en las fotografías vía satélite.


3.2.3 Fuerza ficticia por aceleración angular
Por último, existe una fuerza ficticia adicional
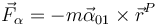
Esta fuerza es menos importante que las dos anteriores, ya que solo aparece en el caso de que la rotación no sea uniforme.
4 Caso general
Cuando el sistema de referencia móvil se traslada a la vez que gira, la aceleración resulta de una combinación de ambos casos

En esta expresión hay que indicar que 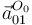 se refiere a la aceleración del origen de coordenadas O0 del sistema móvil, ya que cada punto de ese sistema de referencia tiene una aceleración diferente.
se refiere a la aceleración del origen de coordenadas O0 del sistema móvil, ya que cada punto de ese sistema de referencia tiene una aceleración diferente.





