Fuerzas de rozamiento (GIE)
De Laplace
Contenido |
1 Introducción
Una categoría de fuerzas que aparecen en casi todos los problemas de dinámica, tanto de la partícula como del sólido, es la de las fuerzas de rozamiento. La presencia de estas fuerzas es inevitable, como garantiza el segundo principio de la termodinámica, si bien en ocasiones pueden considerarse como despreciables o ausentes.
Estas fuerzas son difíciles de modelar ya que sus causas son variadas y no obedecen a una teoría física sencilla. Por ello, aquí nos limitaremos a describir cualitativamente los casos más frecuentes.
2 Rozamiento seco
El rozamiento seco es el producido entre dos superficies, no lubricadas, en contacto. El típico ejemplo es un bloque apoyado sobre un plano horizontal o inclinado.
Este rozamiento se produce debido a que los átomos de uno y otro sólido forman pequeños enlaces temporales, que es necesario romper para conseguir el desplazamiento relativo. Estos enlaces se forman debido a las irregularidades del material, a la presión con la que se forma el contacto y al área de la superficie de contacto.
La fuerza de rozamiento seco tiende dos modalidades:
- Rozamiento estático: se produce cuando las dos superficies están en reposo relativo
- Rozamiento dinámico: se da cuando una de las superficies desliza sobre la otra.
2.1 Rozamiento estático
El rozamiento estático posee las siguientes propiedades, conocidas como leyes de Coulomb del rozamiento:
- Es tangente a la superficie de contacto.
- Posee un valor máximo, proporcional a la componente normal de la fuerza aplicada entre los dos cuerpos

- siendo μ una magnitud adimensional conocida como coeficiente de rozamiento estático. Su valor depende de los dos materiales que estén en contacto:
| Material 1 | Material 2 | μ |
|---|---|---|
| Madera | Cemento | 0.6 |
| Madera | Madera | 0.25−0.5 |
| Goma | Cemento | 1.0 |
| Teflón | Teflón | 0.04 |
| Acero | Acero | 0.80 |
Es un error común el pensar que el coeficiente de rozamiento no puede superar a la unidad. Sí, puede hacerlo (el de goma sobre materiales muy abrasivos puede llegar a 4). No hay ningún impedimento físico para que la fuerza de rozamiento supere en módulo a la fuerza normal.
La ley de rozamiento estático nos da un valor máximo para la fuerza de rozamiento, no nos dice cuánto vale ésta.
Supongamos que tenemos un bloque de madera de 5 kg en reposo sobre el suelo de cemento y aplicamos lateralmente una fuerza de 10 N. ¿Se moverá el bloque? El valor máximo de la fuerza de rozamiento es
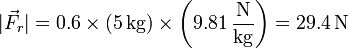
Pero naturalmente eso no es lo que vale la fuerza de rozamiento en este caso concreto, ya que si tuviera dicho valor, superaría a la fuerza aplicada y el bloque se movería en la dirección opuesta a la que se le empuja, lo que es absurdo. Lo que nos dice este resultado es que, puesto que el valor máximo supera a la fuerza aplicada, el bloque no se mueve. La fuerza de rozamiento vale, en este caso, 10 N (igual a la fuerza aplicada).
Si la fuerza aplicada hubiera sido de 40 N, este resultado nos diría que el rozamiento no es capaz de oponerse a la fuerza aplicada y el bloque empieza a moverse, momento a partir del cual se aplica la ley del rozamiento dinámico.
La situación en la que la fuerza de rozamiento alcanza su valor máximo se denomina de deslizamiento inminente, ya que una fuerza aplicada ligeramente superior a las de esta configuración es capaz de conseguir el deslizamiento de las superficies.
Asociado a la fuerza de rozamiento se encuentra el ángulo de fricción β definido por la relación

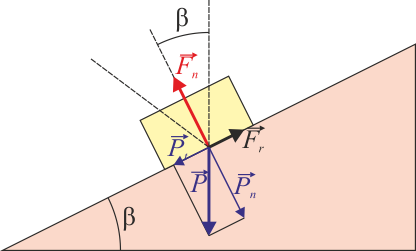
Este ángulo equivale a la mayor inclinación que puede tener un plano inclinado antes de que un bloque situado sobre él comience a deslizar, esto es, se encuentre en posición de deslizamiento inminente. Esta relación permite medir experimentalmente el coeficiente de rozamiento empleando un plano de inclinación variable, que se va elevando lentamente hasta que se produzca deslizamiento.
Gráficamente, el que la fuerza de rozamiento tenga un valor máximo quiere decir que para que la fricción consiga oponerse al resto de fuerzas aplicadas, la resultante de la fuerza normal y la fuerza de rozamiento que sería necesaria para conseguir la anulación del sistema, debe hallarse dentro de un cono con vértice el punto de contacto y de ángulo de apertura β. Si la resultante queda fuera, se produce deslizamiento, ya que la fuerza de rozamiento no puede alcanzar el valor necesario.
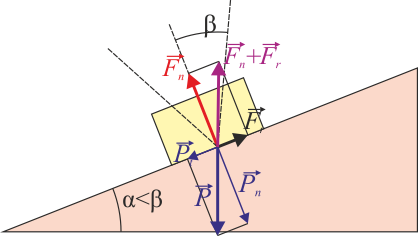
2.2 Rozamiento dinámico
El rozamiento dinámico o por deslizamiento se produce cuando una superficie desliza sobra sobre otra.
Este rozamiento se debe también a los enlaces que se forman entre átomos de ambos materiales. Sin embargo, al ser estos enlaces de menor duración, por el movimiento relativo, la fuerza de rozamiento estático es inferior que la máxima posible en el caso estático.
La fuerza de rozamiento dinámico verifica aproximadamente las siguientes propiedades:
- El proporcional a la fuerza aplicada
- Es independiente de la velocidad relativa
- Va en sentido opuesto a la velocidad relativa
La proporcionalidad puede expresarse por la relación
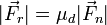
siendo μd el coeficiente de rozamiento dinámico, que será inferior al estático para los mismos materiales. De nuevo, no hay ninguna condición de que sea inferior a la unidad (aunque suele serlo).
| Material 1 | Material | μ |
|---|---|---|
| Madera | Madera | 0.4−0.5 |
| Goma | Cemento | 0.6−0.8 |
| Teflón | Teflón | 0.04 |
| Acero | Acero | 0.16 |
Asociado al coeficiente de rozamiento dinámico se encuentra otro ángulo de rozamiento

que sería el ángulo que debe tener un plano inclinado para que un bloque descienda por él a velocidad constante.
Si representamos conjuntamente la fuerza de rozamiento estático y de rozamiento dinámico, para un bloque, como función de la fuerza tangencial aplicada, obtenemos una gráfica como la de la figura

La pendiente del primer tramo es la unidad, ya que en esa región la fuerza de rozamiento no ha alcanzado su valor máximo y es igual en magnitud a la fuerza aplicada. Cuando se alcanza el deslizamiento inminente se produce un cambio brusco (que es muy fácil de experimentar al desplazar un mueble, por ejemplo) y a partir de ahí la fuerza de rozamiento es más o menos constante, pero con fluctuaciones. La flecha indica que este resultado se consigue aumentando progresivamente la fuerza. Si en lugar de aumentar fuéramos bajando, resultaría una gráfica diferente.
3 Rozamiento por rodadura
El rozamiento por rodadura es el que se produce cuando dos sólidos están en contacto y uno rueda sobre el otro. En una situación ideal de dos sólidos perfectamente indeformables, la rodadura no tendría rozamiento alguno, ya que el contacto se produciría en un solo punto, para el cual la velocidad es nula.
Sin embargo, todos los sólidos son deformables, y en el contacto de una rueda sobre el suelo éste no se produce en un solo punto, sino en una pequeña extensión (mayor cuanto más deformable sea la rueda). Dado que la rueda se encuentra en movimiento pero los puntos en contacto se hallan en reposo instantáneo, se producen esfuerzos en esos puntos, que disipan energía y producen rozamiento.
La fuerza de rozamiento por rodadura obedece también la fórmula

El coeficiente de rozamiento, para ruedas poco deformables, puede ser estimado como
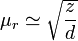
siendo d el diámetro de la rueda y z la “distancia de hundimiento”. Cuanto mayor sea ésta, mayor el rozamiento. Por ello es más barato enviar mercancías por ferrocarril que por camión.
Debido al rozamiento por rodadura hay que vigilar la presión de los neumáticos:
- Si es demasiado baja, aumenta el rozamiento y se consume una cantidad excesiva de energía
- Si es demasiado alta, se hace más difícil frenar un coche, ya que se reduce el área de contacto.
4 Rozamiento viscoso
Un tipo de rozamiento diferente se da en el caso del movimiento de un sólido en el interior de un fluido (líquido o gas). Este rozamiento está causado por las colisiones con las partículas del fluido, que deben ser apartadas para que el sólido pueda moverse por él.
Este rozamiento viscoso depende de numerosos factores:
- De la velocidad del objeto relativa al fluido que le rodea, siendo nulo para un objeto en reposo respecto al fluido.
- De la naturaleza del fluido, en particular de su densidad y de su viscosidad (medida de su cohesión interna del fluido que no debe confundirse con la densidad; el aceite de oliva es más viscoso que el agua, pero menos denso).
- De la forma del objeto. No es lo mismo tirarse de cabeza a una piscina que tirarse en plancha.
La forma matemática de la fuerza de rozamiento viscoso puede ser muy complicada. Los dos casos más simples son:
- Resistencia lineal
- Cuando el fluido es muy viscoso y la velocidad del objeto es pequeña, puede hacerse la aproximación de que la fuerza de rozamiento es proporcional a la velocidad:

- siendo γ una constante empírica, que depende de la forma y tamaño del objeto y de las propiedades del fluido. Se mide en N/(m/s) = kg/s. Para una esfera vale γ = 6πRη (η es la viscosidad); en ese caso se conoce la ley para el rozamiento como ley de Stokes. Aquí
 es siempre la velocidad relativa al fluido. Si este se encuentra en movimiento respecto a un sistema fijo con velocidad
es siempre la velocidad relativa al fluido. Si este se encuentra en movimiento respecto a un sistema fijo con velocidad  habrá que que calcular
habrá que que calcular 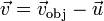 .
.
- Esta fórmula, aunque es muy usada por su simplicidad matemática, posee aplicación limitada, ya que vale para partículas que se mueven lentamente en agua o aceite, pero no es aplicable a cuerpos que se mueven a mayor velocidad, como un barco, o para medios poco densos o viscosos, como el aire.
- Resistencia cuadrática
- Para un objeto que se mueve en aire a una velocidad alta (pero no próximo a la barrera del sonido o supersónica) puede ser una mejor aproximación una ley cuadrática con la velocidad (ley de Rayleigh). En este caso, el módulo de la fuerza es proporcional al cuadrado de la rapidez, su dirección es la misma que la de la velocidad, y su sentido es el opuesto al de éste:

- Estas tres propiedades se pueden reunir en la expreisón vectorial

- Esta ley provoca una mayor complejidad matemática en los cálculos, pero es de mayor aplicabilidad que la anterior. Aquí ρ es la densidad del fluido, A la sección transversal del objeto y Cd el coeficiente de resistencia aerodinámica, empírico. Cuanto más bajo sea Cd más aerodinámico es un objeto (como un coche o una aeronave) y menor su fricción con el aire.
4.1 Velocidad terminal
Cuando un objeto se mueve en un fluido sometido a una fuerza externa constante partiendo del reposo, inicialmente se acelera, aumentando su rapidez, pero al hacerlo se incrementa la fuerza de rozamiento viscoso, que se opone a este aumento, con lo que la aceleración se va reduciendo progresivamente, hasta anularse. A partir de ese momento, la partícula se mueve con velocidad constante, conocida como velocidad terminal o velocidad límite.
Aplicando la segunda ley de Newton queda
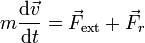
Cuando se alcanza la velocidad límite la aceleración se anula y la fuerza de rozamiento compensa exactamente a la fuerza aplicada
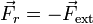
- Rozamiento lineal
- Para velocidades bajas o medios muy viscosos, esta ecuación nos da la velocidad terminal
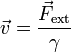
- Esta ecuación nos dice que para medios extremadamente viscosos o velocidades muy bajas, como los que se encuentra una bacteria en su movimiento por el agua, sí se cumple, como decía Aristóteles, que la fuerza es proporcional a la velocidad y que si no se aplica fuerza la partícula se para.
- Para el caso de que la fuerza sea el peso, esta ley nos da para la velocidad límite de caída
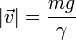
- Rozamiento cuadrático
- Para velocidades medias o altas, la rapidez límite resultante es
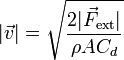
- En el caso particular de la caída de un objeto
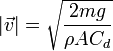
5 Potencia disipada por rozamiento
Cuando la velocidad no es nula, una fuerza de rozamiento (tanto seco como viscoso) desarrolla una potencia
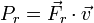
Dado que la fuerza de rozamiento se opone a la velocidad relativa, esta potencia es negativa, esto es, disipa energía.
En el caso del rozamiento seco dinámico, es proporcional a la rapidez
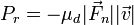
En el caso del rozamiento viscoso lineal, la disipación va como el cuadrado de la celeridad
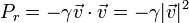
esto es, doble de velocidad implica cuádruple de energía disipada por unidad de tiempo.
En el caso del rozamiento viscoso cuadrático, la potencia va como el cubo de la rapidez: doble de velocidad, óctuple de potencia disipada
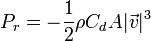
Esta energía disipada se transmite como calor, aumentando la temperatura de las superficies de contacto y llegando en ocasiones a su fusión (el “gripado” de los motores). Por ello es importante reducir la fricción en máquinas y mecanismos.






