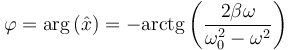Fasor (GIE)

De Laplace

Contenido

1 Fórmula de Euler
2 Producto por una exponencial de un número imaginario
3 Vectores rotatorios
4 Amplitudes complejas (fasores)
5 Derivación e integración de fasores
- 5.1 Velocidad en un MAS
- 5.2 Aceleración en un MAS
6 Integración de fasores
7 Aplicación al caso de un oscilador forzado

1 Fórmula de Euler

Existe una forma expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas

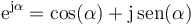
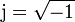
$\mathrm{e}^{\mathrm{j}\alpha} = \cos(\alpha)+\mathrm{j}\,\mathrm{sen}(\alpha)$ $\mathrm{j}=\sqrt{-1}$

o, equivalentemente,

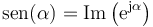
$\cos(\alpha) = \mathrm{Re}\left(\mathrm{e}^{\mathrm{j}\alpha}\right)$ $\mathrm{sen}(\alpha) = \mathrm{Im}\left(\mathrm{e}^{\mathrm{j}\alpha}\right)$

Gráficamente esta igualdad significa que la exponencial de un número imaginario es un vector en el plano complejo, siendo este vector de módulo unidad y que forma un ángulo $α$ con el eje real.

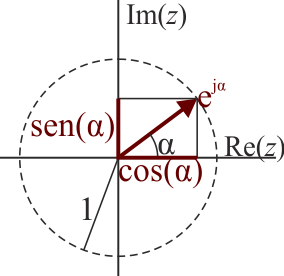
Como casos particulares importantes tenemos

$\mathrm{e}^{\mathrm{j}\pi/2}=\mathrm{j}\qquad\qquad \mathrm{e}^{\mathrm{j}\pi}=-1$

La segunda, escrita en la forma

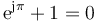
$\mathrm{e}^{\mathrm{j}\pi}+1 = 0\,$

está considerada como una de las fórmulas más bellas de las matemáticas por reunir los números más importantes: 0, 1, π, e y j (o i) en una sola expresión.

2 Producto por una exponencial de un número imaginario

La fórmula de Euler puede extenderse a cualquier número complejo, ya que

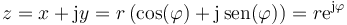
$z = x + \mathrm{j}y = r\left(\cos(\varphi)+\mathrm{j}\,\mathrm{sen}(\varphi)\right)=r\mathrm{e}^{\mathrm{j}\varphi}$

siendo $r = | z |$ el módulo del número complejo y $\varphi$ su argumento. Gráficamente se ve que esta es otra forma de presentar las coordenadas polares descritas en cinemática.

Cuando se multiplica un número complejo cualquiera por la exponencial de un número imaginario tenemos que

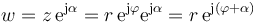
$w = z\,\mathrm{e}^{\mathrm{j}\alpha} = r\,\mathrm{e}^{\mathrm{j}\varphi}\mathrm{e}^{\mathrm{j}\alpha}=r\,\mathrm{e}^{\mathrm{j}(\varphi+\alpha)}$

Vemos que el resultado es otro número complejo con el mismo módulo que el original, pero cuyo argumento se ha incrementado en la cantidad $α$ . Es decir, la multiplicación por la exponencial de un número imaginario equivale a una rotación en el plano complejo.

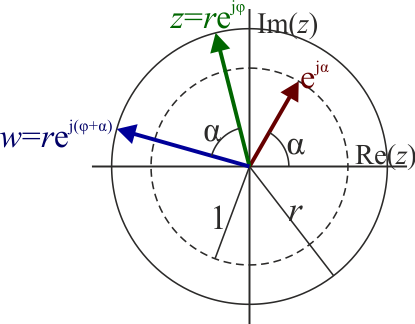
En particular:

La multiplicación de un número complejo por la unidad imaginaria $j$ equivale a una rotación de 90° en el plano complejo.
La multiplicación de un número complejo por −1 (igual a $j 2$ ) equivale a una rotación de 180° en el plano complejo.

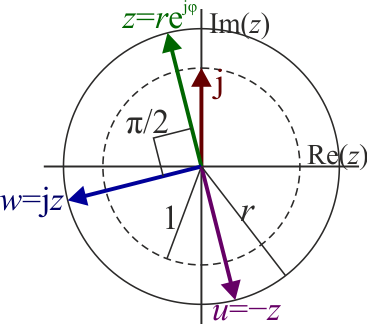
3 Vectores rotatorios

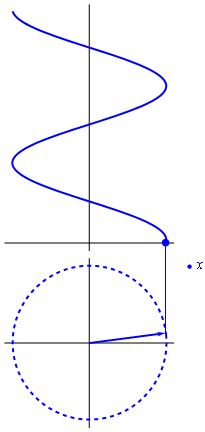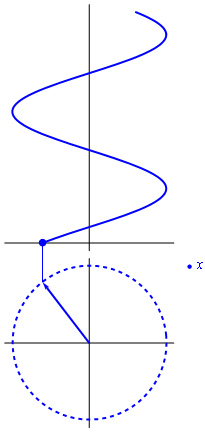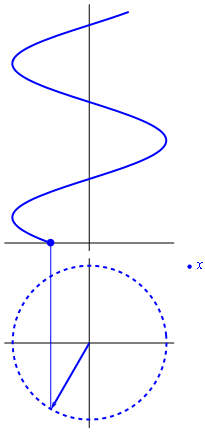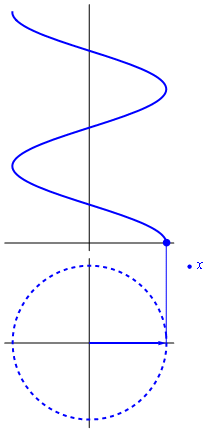
Si consideramos ahora que el exponente en la fórmula de Euler no es una cantidad fija, sino que aumenta con el tiempo, el resultado es un vector rotatorio en el plano complejo

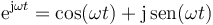
$\mathrm{e}^{\mathrm{j}\omega t} = \cos(\omega t)+\mathrm{j}\,\mathrm{sen}(\omega t)$

La parte real de este número complejo rotatorio, esto es, su proyección sobre el eje de abscisas, representa una oscilación cosenoidal. La parte imaginaria oscila igualmente, pero como un seno, esto es, desfasada un cuarto de periodo.

4 Amplitudes complejas (fasores)

La solución general del movimiento armónico simple, en función de las condiciones iniciales, es

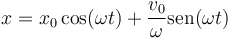
$x = x_0\cos(\omega t) + \frac{v_0}{\omega}\mathrm{sen}(\omega t)$

y, en función de la amplitud y la fase

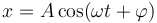
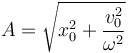
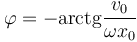
$x = A\cos(\omega t+\varphi)\,$ $A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$ $\varphi=-\mathrm{arctg}\frac{v_0}{\omega x_0}$

Aplicando la fórmula de Euler a la expresión anterior

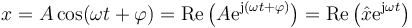
$x = A \cos(\omega t + \varphi) = \mathrm{Re}\left(A \mathrm{e}^{\mathrm{j}(\omega t + \varphi)}\right) = \mathrm{Re}\left(\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

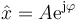
$\hat{x}=A\mathrm{e}^{\mathrm{j}\varphi}$

es la llamada amplitud compleja o fasor de la variable $x$ . El movimiento armónico simple se puede ver entonces como la proyección sobre el eje real de un vector que gira en el plano complejo y cuyo valor en el instante $t = 0$ es la amplitud compleja 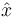$\hat{x}$ .

Se define entonces, en general, la amplitud compleja o fasor 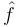$\hat{f}$ de una cantidad oscilante $f (t)$ como aquel número complejo constante que cuando se multiplica por $e jω t$ y se halla la parte real del producto, resulta la cantidad $f (t)$ .

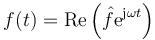
$f(t) = \mathrm{Re}\left(\hat{f}\mathrm{e}^{\mathrm{j}\omega t}\right)$

Este número complejo tiene por módulo la amplitud de las oscilaciones y por argumento la constante de fase

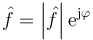
$\hat{f} = \left|\hat{f}\right|\mathrm{e}^{\mathrm{j}\varphi}$

Aplicando de nuevo la fórmula de Euler al caso del MAS obtenemos la parte real y la imaginaria del fasor de la posición

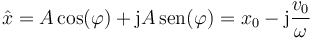
$\hat{x}= A\cos(\varphi)+\mathrm{j}A\,\mathrm{sen}(\varphi)= x_0-\mathrm{j}\frac{v_0}{\omega}$

esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales del movimiento.

5 Derivación e integración de fasores

La gran ventaja de la definición de los fasores es que simplifican enormemente las derivadas e integrales.

5.1 Velocidad en un MAS

Si derivamos la expresión fasorial obtenemos la velocidad instantánea de una partícula en un MAS

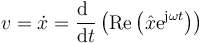
$v = \dot{x}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{Re}\left(\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)\right)$

La derivada de una parte real es la parte real de la derivada, y 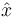$\hat{x}$ es una cantidad constante, por lo que

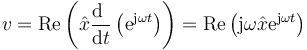
$v = \mathrm{Re}\left(\hat{x}\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\mathrm{e}^{\mathrm{j}\omega t}\right)\right) = \mathrm{Re}\left(\mathrm{j}\omega\hat{x}\mathrm{e}^{\mathrm{j}\omega t}\right)$

Esto es, la velocidad también se puede escribir en forma fasorial

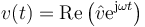
$v(t) = \mathrm{Re}\left(\hat{v}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

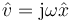
$\hat{v}=\mathrm{j}\omega \hat{x}$

es decir, para calcular el fasor de la derivada de una magnitud, solo necesitamos multiplicar el fasor de dicha magnitud por $jω$ . El uso de fasores transforma las derivadas en multiplicaciones.

En función de las condiciones iniciales el fasor de la velocidad es

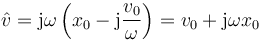
$\hat{v}=\mathrm{j}\omega\left(x_0-\mathrm{j}\frac{v_0}{\omega}\right) = v_0+\mathrm{j}\omega x_0$

Podemos comprobar que efectivamente este fasor produce la velocidad como función del tiempo

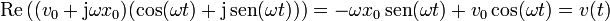
$\mathrm{Re}\left((v_0+\mathrm{j}\omega x_0)(\cos(\omega t)+\mathrm{j}\,\mathrm{sen}(\omega t))\right)=-\omega x_0\,\mathrm{sen}(\omega t)+v_0\cos(\omega t) = v(t)$

El resultado es la derivada temporal de la posición.

En el plano complejo, el fasor de la velocidad está girado 90° respecto al de la posición, como resultado de la multiplicación por la unidad imaginaria.

5.2 Aceleración en un MAS

La misma regla algebraica la podemos aplicar al cálculo de la aceleración. Su fasor será igual al de la velocidad multiplicado por $jω$

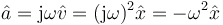
$\hat{a}=\mathrm{j}\omega\hat{v}=(\mathrm{j}\omega)^2\hat{x}=-\omega^2\hat{x}$

Gráficamente el fasor de la aceleración está girado 90° respecto al de la velocidad y por tanto posee sentido opuesto al de la posición.

6 Integración de fasores

La regla inversa a la de la derivación se aplica a la hora de integrar. Si se sabe que tanto una magnitud como su primitiva son funciones oscilantes, el fasor de la primitiva es simplemente el fasor de la magnitud dividido por $jω$ . Así

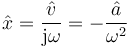
$\hat{x}=\frac{\hat{v}}{\mathrm{j}\omega}=-\frac{\hat{a}}{\omega^2}$

7 Aplicación al caso de un oscilador forzado

Un ejemplo en el que la solución empleando fasores es mucho más simple que la que usa funciones trigonométricas es el caso de un oscilador armónico con rozamiento sometido a una fuerza oscilante.

Suponemos un oscilador armónico unidimensional, de constante $k$ , masa $m$ y coeficiente de rozamiento viscoso $b$ . Se trata de ver cómo se mueve este oscilador cuando se encuentra sometido a una fuerza

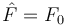
$F(t)=F_0\cos(\omega t)=\mathrm{Re}\left(\hat{F}\mathrm{e}^{\mathrm{j}\omega t}\right)$ $\hat{F}=F_0$

La ecuación de movimiento para la partícula es

$ma=-kx-bv+F_0\cos(\omega t)\,$

o, en términos de la posición,

$\ddot{x}+2\beta\dot{x}+\omega_0^2 x = \frac{F_0}{m}\cos(\omega t)\qquad\qquad \beta=\frac{\gamma}{2m}\qquad \omega_0=\sqrt{\frac{k}{m}}$

Tras un periodo transitorio inicial, el movimiento de la partícula se reduce a oscilaciones siguiendo a la fuerza, con la misma frecuencia, pero con un posible desfase

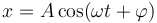
$x=A\cos(\omega t + \varphi)\,$

Para encontrar la amplitud y desfase de este movimiento oscilatorio, escribimos la ecuación la ecuación en forma fasorial, reemplazando las derivadas por multiplicaciones por $jω$ . Nos queda la ecuación algebraica

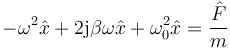
$-\omega^2\hat{x} +2\mathrm{j}\beta\omega\hat{x}+\omega_0^2\hat{x}=\frac{\hat{F}}{m}$

De aquí despejamos el fasor de la posición

$\hat{x}=\frac{\hat{F}/m}{(\omega_0^2-\omega^2)^2+2\mathrm{j}\beta \omega}$

Esta ecuación nos da la amplitud de las oscilaciones

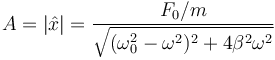
$A = |\hat{x}| = \frac{F_0/m}{\sqrt{(\omega_0^2-\omega^2)^2 + 4\beta^2\omega^2}}$

y el desfase respecto a la fuerza aplicada

$\varphi =\arg\left(\hat{x}\right) = -\mathrm{arctg}\left(\frac{2\beta\omega}{\omega_0^2-\omega^2}\right)$

Fasor (GIE)

De Laplace

Contenido

1 Fórmula de Euler

2 Producto por una exponencial de un número imaginario

3 Vectores rotatorios

4 Amplitudes complejas (fasores)

5 Derivación e integración de fasores

5.1 Velocidad en un MAS

5.2 Aceleración en un MAS

6 Integración de fasores

7 Aplicación al caso de un oscilador forzado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES