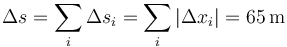Velocidad dependiente del tiempo (GIOI)
De Laplace
Contenido |
1 Enunciado
Una partícula describe un movimiento rectilíneo cuya velocidad, como función del tiempo entre  y
y  es la parábola de la figura.
es la parábola de la figura.
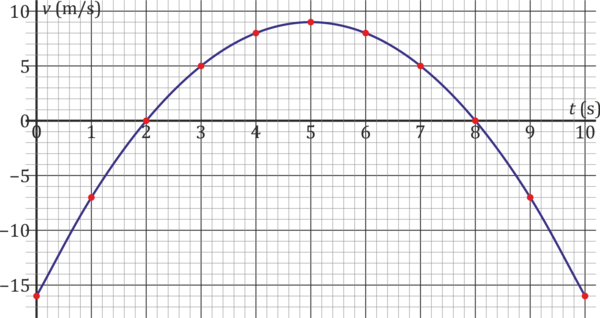
- ¿Cuánto vale, aproximadamente, el desplazamiento neto en el intervalo [0s, 10s]?
- ¿Cómo es la gráfica de la aceleración de la partícula?
- ¿En qué intervalos, en s, la partícula está frenando?
- ¿Cuánto vale, aproximadamente, la rapidez media en el intervalo [0s, 10s]?
2 Desplazamiento neto
Hallamos primero la ecuación de la velocidad como función del tiempo. Por ser una parábola es de la forma

Como se anula en t = 2 y t = 8 (segundos, usamos unidades fundamentales del SI) y en t = 0 vale -16, queda
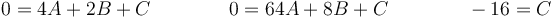
Restando
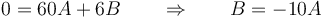
Sustituimos
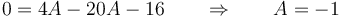
Por tanto la parábola es de la forma
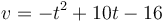
Integramos respecto al tiempo para hallar el desplazamiento

La velocidad media en este intervalo es

3 Gráfica de la aceleración
La velocidad es una función cuadrática, por lo que la aceleración, su derivada, debe ser una recta. Además, la velocidad es creciente en la primera mitad del intervalo y decreciente en la segunda, por lo que la aceleración debe ser poitiva en la primera mitad y negativa en la segunda. Por ello, su gráfica es la B.
Evidentemente, también puede demostrarse derivando respecto al tiempo la expresión de la velocidad.
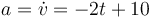
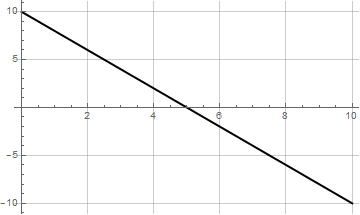
4 Frenado de la partícula
El frenado de la partícula corresponde a que su rapidez esté disminuyendo. Gráficamente esto corresponde a que la curva de la velocidad se esté acercando al eje v=0. Esto ocurre en dos intervalos
- Entre t = 0s y t = 2s.
- Entre t = 5s y t = 8s.
5 Rapidez media
La rapidez media se calcula como la distancia total recorrida dividida por el intervalo empleado.
La distancia recorrida la calculamos dividiendo el intervalo en tres tramos, según el signo de la velocidad
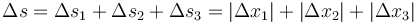
- El primer tramo es entre t = 0s y t = 2s, en el que la velocidad es negativa
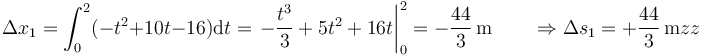
- El segundo entre t=2s y t = 8s, en los que v >0
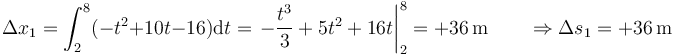
- El tercero entre t=8s y t = 10s, en los que vuelve a ser negativa
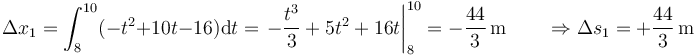
Sale lo mismo que en el primero por la simetría de la curva.
Sumando las tres contribuciones tenemos la distancia total recorrida
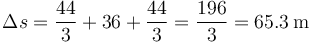
y la rapidez media
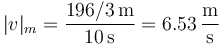
6 Solución numérica
Este problema puede servir para ilustrar los métodos numéricos aproximados, para lo que conviene tener a mano un programa como Excel.
En lugar de buscar primero la ecuación de la parábola y luego integrar analíticamente, puede calcularse la integral aproximada sustituyendo la curva por una serie de tramos rectos que unen los puntos marcados. La integral, para cada tramo es el área de un trapecio
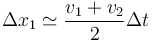
En cada uno de los tramos, el intervalo de tiempo es el mismo, un segundo, mientras que las velocidades valen
| t (s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| v (m/s) | -16 | -7 | 0 | 5 | 8 | 9 | 8 | 5 | 0 | -7 | -16 |
Esto nos da los sucesivos desplazamientos, calculados en cada caso con la fórmula anterior
| Δt (s) | 0-1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | 8-8 | 9-10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \Delta x (m) | -11.5 | -3.5 | +2.5 | +1.5 | +0.5 | +0.5 | +1.5 | +2.5 | -3.5 | -11.5 |
| \Delta s (m) | 11.5 | 3.5 | 2.5 | 1.5 | 0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 11.5 |
Sumando todos los desplazamientos, obtenemos un desplazamiento total aproximados
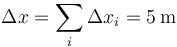
y una distancia total recorrida