Transmisión del calor
De Laplace
Contenido |
1 Introducción
(Apéndice del tema 2 de Çengel & Bole, “Temas de especial interés”)
En los apartados anteriores se ha hablado del calor como de una transferencia de energía no asociada a variaciones en variables macroscópicas, pero no se ha dicho nada de cómo se transmite esa energía. Esto es, en el caso del trabajo uno “ve” cómo se realiza el trabajo (en el caso mecánico) o al menos posee un modelo del proceso (en el caso eléctrico), pero ¿cómo se transfiere el calor? ¿Cómo pasa esa energía de un cuerpo a otro?
Al estar asociado a variables microscópicas, cualquier descripción de la transferencia de calor debe basarse en el estudio de las colisiones e interacciones entre las moléculas de las diferentes sustancias, así como de la radiación que emiten (estando la radiación infrarroja usualmente asociada a la temperatura del cuerpo).
Independientemente de que se elabore un modelo microscópico más o menos detallado de las sustancias, sí pueden describirse las formas en que el calor se transmite de un cuerpo a otro. Estos mecanismo son:
- Conducción
- Convección
- Radiación
Estos mecanismos no son incompatibles entre sí y de hecho es habitual que se den simultáneamente.
2 Conducción
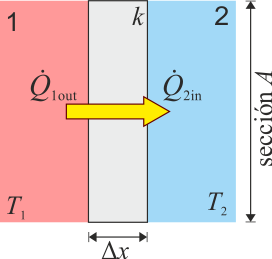
La transmisión de calor por conducción se da cuando se ponen en contacto dos materiales a diferente temperatura.
La agitación térmica es mayor en el de temperatura más elevada, por lo que cuando se produce un choque de una de las moléculas de la superficie del más caliente con una de las moléculas superficiales del más frío, el que se movía más rápido pierde algo de su energía y el más lento la gana. El resultado es que la temperatura del más caliente disminuye y la del más frío aumenta. Se produce un flujo de energía a través de la superficie de contacto, que identificamos como calor.
En su modelo más sencillo, suponemos que tenemos una lámina de un cierto material (por ejemplo, el vidrio de una ventana) a uno de cuyos lados se encuentra un sistema a una temperatura T2 (por ejemplo, la calle a 15°C) y al otro uno a temperatura T2 (la habitación, a 22°C). Se produce entonces un flujo de calor 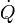 (¡ojo al punto!) desde el sistema a mayor temperatura al de menor. ¿De qué depende este flujo de calor?
(¡ojo al punto!) desde el sistema a mayor temperatura al de menor. ¿De qué depende este flujo de calor?
- De la diferencia de temperaturas ΔT = T2 − T1, cuánto mayor sea ésta, más grande es el flujo de calor.
- Del espesor del material intermedio, Δx. Cuanto más grueso sea, menos calor fluye.
- Del área A del material. Por una ventana grande fluye más calor que por un ventanuco.
- De la naturaleza del material intermedio. No fluye el mismo calor a través de una lámina metálica que a través de una de aislante de fibra de vidrio.
Todas estas propiedades se resumen en la siguiente fórmula, conocida como ley de Fourier:
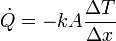
donde 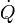 es el flujo de calor considerando que va del medio 1 al 2, es decir, sería
es el flujo de calor considerando que va del medio 1 al 2, es decir, sería
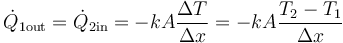
Si T1 > T2 entonces ΔT > 0 y el signo es positivo, como corresponde. Si T2 > T1 resulta un valor negativo, lo que implica que en ese caso el calor va del medio 2 al 1, como cabe esperar. Jugando con los signos, podemos escribir esta relación de forma simétrica apara los dos medios:
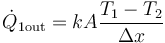
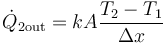
es decir, el calor que escapa de un sistema es proporcional a la diferencia entre la temperatura de ese sistema y la de lo que le rodea.
La constante k es una propiedad de cada material denominada conductividad térmica. Se mide en el SI en W/(K·m). Valores aproximados para algunos materiales conocidos son
| Material | k (W/(K·m)) | Material | k (W/(K·m)) | Material | k (W/(K·m)) |
|---|---|---|---|---|---|
| Aire seco | 0.024 | Agua | 0.58 | Cobre | 385.0 |
| Lana | 0.04 | Ladrillo | ∼0.6 | Hierro | 80 |
| Microfibra | 0.033 | Madera | ∼0.15 | Vidrio | 0.96 |
Vemos que los metales son excelentes conductores del calor, mientras que los tejidos y el aire son aislantes térmicos.
Es la conductividad térmica y no la temperatura la que provoca que al pisar el suelo al levantarnos nos parezca frío, mientras que una zapatilla nos parece caliente. El suelo y la zapatilla están a la misma temperatura, pero mientras el calor se escapa de nuestros pies por el suelo, queda bloqueado por la zapatilla. Por la misma razón sería incorrecto hablar del calor que dan las mantas. Una manta actúa como un aislante térmico para que no se escape el calor humano, pero no producen calor por sí mismas.
2.1 Distribución de temperaturas
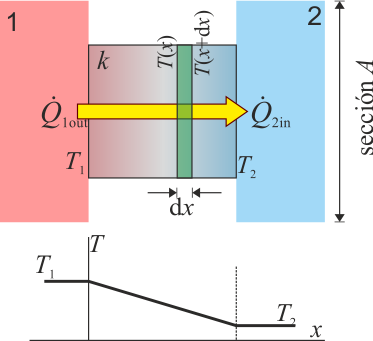
Consideremos el caso de una barra metálica, uno de cuyos extremos está en contacto con una fuente de calor, mientras que el otro se encuentra sumergido en agua con hielo. Sabemos que se producirá un flujo de calor a través del metal desde la fuente de calor hasta el sumidero, pero podemos decir más: la temperatura de la barra metálica no será la misma en todos los puntos (no estará, por tanto, en equilibrio térmico), sino que varía gradualmente desde su valor mínimo al máximo.
Si consideramos un corte de la barra de espesor diferencial dx, el flujo de calor que lo atraviesa cumplirá la ley de Fourier, pero para una diferencia de temperaturas muy pequeña (la que hay entre x y x + dx), con lo que obtenemos una relación con la derivada de la temperatura respecto a la posición
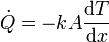
Esta se conoce también como ley de Fourier y nos permite determinar, con las condiciones adecuadas, cuál es la distribución de temperaturas dentro de un sistema en presencia de flujos de calor.
En el caso de una capa de material situada entre dos focos a diferente temperatura, el resultado es que la temperatura varía linealmente con la posición.
2.2 Resistencia térmica
En el caso anterior de una lámina entre dos sistemas a diferente temperatura, existe una relación de proporcionalidad entre flujo de calor y temperatura que se puede escribir
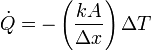
La cantidad entre paréntesis no depende de la diferencia de temperaturas sino solo de las propiedades físicas y las dimensiones del material. A la inversa de este factor se lo denomina resistencia térmica de la lámina
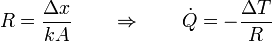
La resistencia térmica (que se mide en K/W) es una medida de la oposición al paso de calor. Cuanto mayor es el espesor de la lámina, menor su conductividad térmica o su área, menor es el flujo de calor. Un recubrimiento que tenga una resistencia térmica muy alta será un buen aislante térmico (una pared adiabática), mientras que si es muy baja (un envase metálico, por ejemplo) constituirá una pared diaterma.
- Resistencias en paralelo
- Consideremos el caso de una habitación. Parte de su frontera será ladrillo, parte vidrio, parte madera… El flujo de calor que entra en la habitación será la suma del que atraviesa cada uno de los materiales
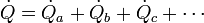
- Si todo el interior está a la misma temperatura Tint y todo el exterior a una sola temperatura exterior Text, entonces la diferencia de temperaturas a los lados de cada material es la misma para todos ellos
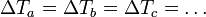
- Por tanto nos queda
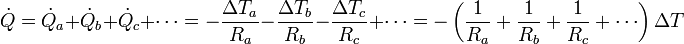
- Si consideramos la resistencia del conjunto de la frontera verifica
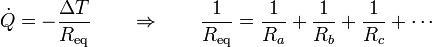
- Por tanto, cuando tenemos resistencias térmicas en paralelo, la inversa de la resistencia equivalente es igual a la suma de las respectivas inversas.
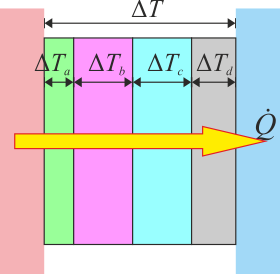
- Resistencias en serie
- Consideremos ahora varias capas puestas a continuación una de la otra, como pueden ser una sábana, dos mantas y un edredón. En este caso, no se cumple que el flujo de calor sea la suma de los flujos individuales, sino por el contrario, que el mismo calor que atraviesa la sábana, atraviesa las mantas y el edredón
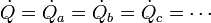
- La diferencia de temperaturas en cambio, será la suma de las sucesivas diferencias de temperatura
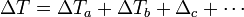
- esto nos da la relación
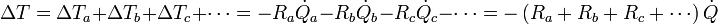
- según la cual la resistencia térmica equivalente a varias capas puestas en serie es la suma de las resistencias respectivas
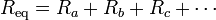
El efecto entonces de colocar diversas capas sobre la piel no es reducir la diferencia de temperaturas con el exterior, que permanece constante, sino disminuir el flujo de calor. El calor que escapa del cuerpo debe ser repuesto por el organismo a partir de su metabolismo. Si este flujo es excesivo, el cuerpo no es capaz de compensarlo y sobreviene la hipotermia.
3 Convección
A la vista de las conductividades térmicas de la tabla anterior, es claro que el aire es más aislante que los tejidos, con lo cual surge la pregunta, ¿por qué nos vestimos? ¿por qué es necesario taparse con una manta en invierno, si el aire es más aislante que la lana?
La razón es que en un sistema fluido, como un gas o un líquido, la conducción no es el único mecanismo de transmisión de calor. Además de este, está presente la convección, que es la transferencia de energía arrastrada por el propio movimiento del fluido.
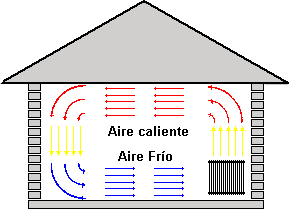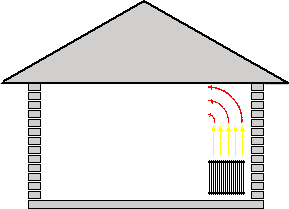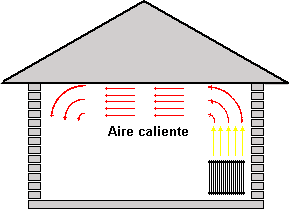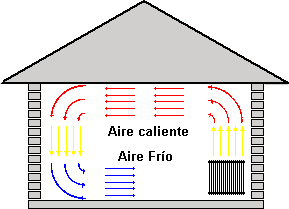
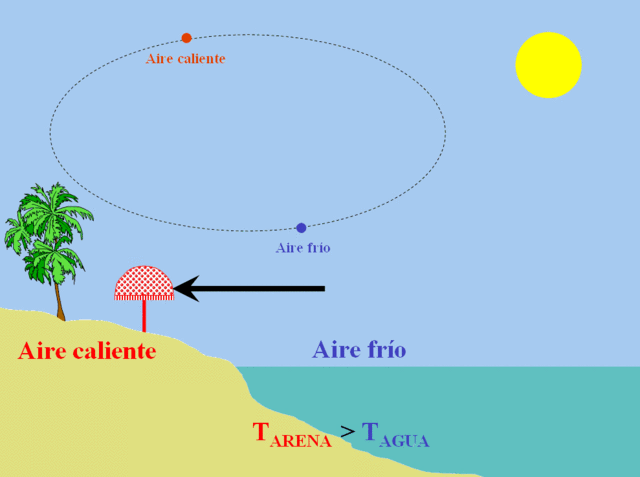
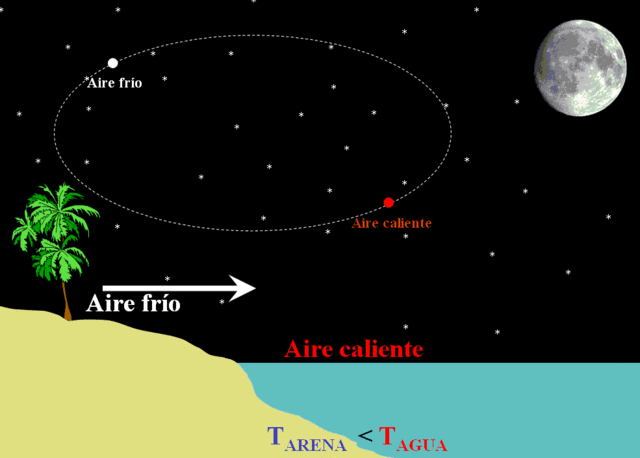
Consideremos el caso de una habitación, en la cual se encuentra un radiador, que calienta el aire a su alrededor. Si tuviéramos que esperar que el calor llegara por conducción al otro lado de la habitación, probablemente podríamos morir congelados. Lo que ocurre en realidad es que, al ser el aire caliente menos denso que el frío, asciende hacia el techo de la habitación, creando una depresión que es llenada por aire frío, el cual es calentado a su vez, continuando el proceso. Se establece así una circulación de corriente en forma de rollo. El efecto neto es la transmisión de calor desde el radiador hasta el otro extremo de la habitación. A este fenómeno se lo denomina “convección” y al movimiento del aire (o del fluido en general) se lo denomina “corriente de convección”.
Las corrientes de convección son responsables de fenómenos como la brisa, que durante el día va desde el mar hacia la tierra y durante la noche a la inversa.
También son las causantes de la deriva de los continentes, arrastrados por las corrientes de convección del manto.
No es posible escribir una ecuación sencilla para la cantidad de calor transportada por convección, ya que depende de la solución del problema de dinámica de fluidos que implica el estudio de las corrientes de convección.
Cuando las corrientes de convección se producen espontáneamente, por la acción de la gravedad, la convección se denomina libre (o natural). Si es causada por algún agente externo, como un ventilador, se llama “convección forzada”.
La razón entonces de las mantas en invierno es tanto funcionar como aislante térmico como impedir que el aire en las proximidades del cuerpo humano escape. Sin ningún tipo de abrigo, el aire caliente próximo al cuerpo asciende por convección y es sustituido por aire frío, refrigerando el organismo.
Inversamente, el efecto de un ventilador en verano es forzar la convección y refrescar el cuerpo sustituyendo el aire caliente y húmedo que lo rodea por aire más fresco y seco (en este caso también es muy importante el efecto de la evaporación ya que, como se ha dicho, el cambio de fase requiere una gran cantidad de calor, que se extrae del organismo).
4 Radiación
El tercer mecanismo de transmisión de calor es la radiación. Todo cuerpo, por estar a una cierta temperatura, emite ondas electromagnéticas, pudiendo también absorberlas. La emisión de estas ondas por un cuerpo y su absorción por otro implica una transmisión de energía que identificamos como calor.
La longitud de onda y la potencia relativa de la radiación emitida depende de la temperatura del cuerpo, según la llamada ley del cuerpo negro. Para las temperaturas habituales a nuestro alrededor, la mayor parte de esta radiación está en la banda de infrarrojos. Por ello, las cámaras de visión nocturna y los termogramas se basan en la detección de radiación infrarroja, de forma que se asocia un calor a cada longitud de onda y por tanto a cada temperatura.
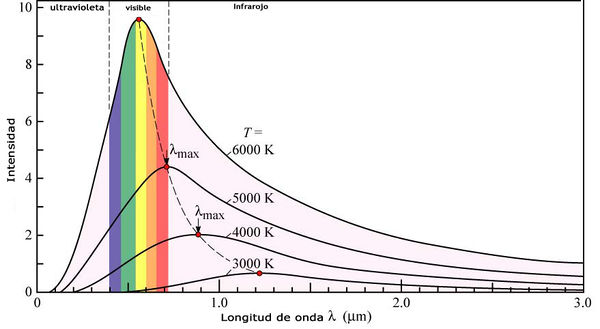

Para cuerpos a altas temperaturas, la radiación térmica emitida entra en el espectro visible y por ello tenemos “hierro al rojo vivo”. Una mayor temperatura supone emisión centrada en el naranja (como en el Sol) o incluso en colores de longitudes de onda más corta. De esta forma, a partir del color de una estrella se conoce su temperatura exterior.
La potencia emitida por un cuerpo en forma de radiación depende su temperatura según la llamada ley de Stefan-Boltzmann. Para un cuerpo negro ideal
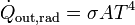
donde A es el área del cuerpo y
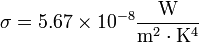
es una constante universal conocida como constante de Stefan-Boltzmann. En un cuerpo real, la radiación emitida nunca alcanza este valor, por lo que se escribe
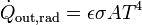
siendo ε una cantidad entre 0 y 1 denominada emisividad del cuerpo. El que la potencia radiada vaya como la cuarta potencia de la temperatura absoluta quiere decir que a bajas temperaturas el calor emitido o absorbido por radiación puede ser despreciable, pero a altas temperaturas puede ser el factor dominante.
La emisión por radiación no puede ser impedida nunca de manera completa, ya que el simple hecho de tener una temperatura provoca emisión de radiación. Por ello es imposible construir unas paredes totalmente adiabáticas. Sí puede ser reducida con ayuda de paredes reflectantes que devuelvan parte de la radiación emitida (por ello, las paredes de la cámara de los termos o vasos Dewar están metalizadas).
Si consideramos un cuerpo a temperatura T1 rodeado de un ambiente a temperatura T0, el calor que entra en el cuerpo por radiación será
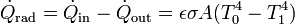
Si la temperatura del entorno es superior a la del cuerpo se produce absorción neta de calor por radiación, mientras que si el cuerpo está a mayor temperatura que el ambiente es a la inversa, como cabe esperar.
Las pérdidas de energía por radiación son responsables del “relente”: el fenómeno de que en una noche despejada un objeto situado en la calle (un coche aparcado, por ejemplo) puede estar más frío que el aire circundante. La razón de este desequilibrio térmico se debe a que en este caso el “entorno” es el vacío interplanetario, que se encuentra a una temperatura de 2.7K. Por ello, la radiación que emite el vehículo hacia el espacio es mucho mayor que la que puede recibir de él y se produce un enfriamiento continuado. Si desapareciera el Sol, este efecto congelaría la Tierra entera rápidamente.



El relente no se produce en una noche cubierta, ya que en ese caso la radiación emitida por el coche se refleja en las nubes, que funcionan como entorno. Aunque las nubes también se enfrían, la capa de aire entre ellas y el suelo mantiene una temperatura mucho más alta que en el caso de una noche despejada.