Trabajo en un gas con resorte
De Laplace
Contenido[ocultar] |
1 Enunciado
Se tiene un cilindro de sección S en el interior del cual hay un pistón que puede deslizarse sin rozamiento. El pistón cierra una cámara en la que hay aire. La cara exterior del pistón está unida al extremo del tubo mediante un resorte de constante k y longitud natural l0. Esta parte del tubo está abierta a la atmósfera. Para un cierto valor de la temperatura, T0, la presión es la atmosférica, el pistón se encuentra a una distancia h0 del fondo y el resorte no ejerce fuerza alguna. Cuando el gas se calienta, se expande y el resorte se comprime.
- Halle el trabajo realizado sobre el gas cuando la posición del pistón pasa de x0 = 0 a x.
- Calcule la variación de la energía interna del gas y el calor transferido al gas en el proceso.
- Calcule el trabajo, la variación en la energía total y el calor, si consideramos que el sistema esta formado por el gas y el muelle.
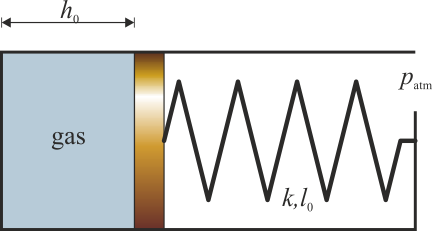
2 Trabajo sobre el gas
El trabajo realizado sobre un gas se calcula mediante la integral
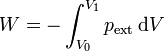
Cuando el émbolo se encuentra a una distancia x de su posición inicial, el volumen ocupado por el gas es
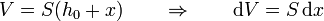
El muelle se ha comprimido en esta distancia y la presión externa sobre el gas es
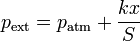
por lo que el trabajo en una expansión del gas vale
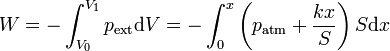
Integrando esta función en la que la única variable es la posición x

Para poner este resultado en función de la temperatura se aplica que existe una relación entre la temperatura y la posición del émbolo, que se obtiene por la ley de los gases ideales
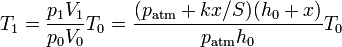
3 Energía interna y calor
3.1 Energía interna
La energía interna de un gas ideal depende exclusivamente de su temperatura, siendo su incremento
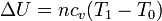
En el caso del aire, se puede tratar como un gas diatómico, con capacidad calorífica molar cv = 5R / 2, o, más en general
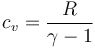
lo que nos da el incremento de energía interna
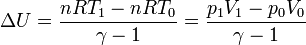
En función de la posición del pistón, sustituyendo las presiones y los volúmenes,
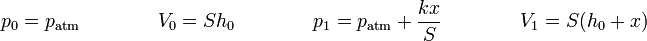
queda

3.2 Calor
Una vez que tenemos el trabajo y la variación de la energía interna, hallamos el calor por el primer principio de la termodinámica
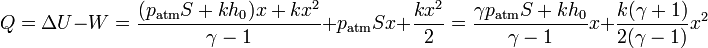
El calor que entra en el sistema se emplea en dos funciones:
- Incremento de la energía interna
- Trabajo realizado por el gas, que a su vez se divide en:
- Expansión del gas contra la presión atmosférica
- Expansión del gas contra el resorte.
4 Sistema incluyendo el resorte
4.1 Trabajo
Si contamos el muelle como parte del sistema, entonces el trabajo es la suma del que se realiza contra el gas
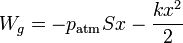
más el que se realiza contra el muelle. El trabajo sobre el muelle se almacena como energía potencial elástica
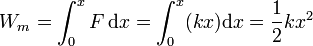
Ponemos +kx y no -kx porque hemos hallado el trabajo de la fuerza que se ejerce sobre el muelle, que será igual y opuesta a la que este produce.
El trabajo total sobre el sistema es entonces
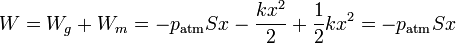
es decir, el trabajo total es sólo el que se hace contra la presión atmosférica.
4.2 Energía
Al existir una energía potencial en el sistema, para aplicar el primer principio de la termodinámica ya no debemos hablar de la energía interna, sino de la energía total
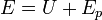
cuyo incremento en este caso vale

Poniéndolo en función de la posición
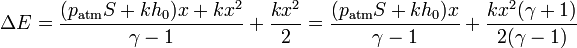
4.3 Calor
Aplicando el primer principio nos queda exactamente el mismo calor que en el cálculo anterior
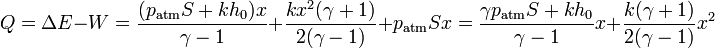
Esto era de esperar pues en el resorte no entra calor, por lo que solo hay que contar el que llega al gas, que será el mismo se calcule como se calcule.
En este caso, el calor que entra en el sistema se emplea en
- Incremento de la energía total, que se divide en:
- Aumento de la energía interna del gas
- Compresión del muelle
- Trabajo realizado por el sistema, solo contra la presión atmosférica
Vemos que, aunque el balance sigue manteniéndose, un término que antes se contaba como trabajo, ahora se incluye como energía.





