Teorema de Gauss
De Laplace
1 Enunciado
El flujo de un campo a través de una superficie cerrada y la divergencia están estrechamente relacionados a través del Teorema de Gauss
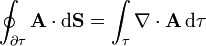
que nos dice que la cantidad de campo que escapa hacia el exterior de una superficie cerrada 
es igual a la suma neta de las fuentes escalares contenidas en el interior de dicha superficie.
