Rotación instantánea de un sólido rígido
De Laplace
Contenido |
1 Introducción
El campo de velocidades de un sólido rígido tiene la forma
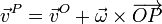
Un caso particular importante se da cuando existe al menos un punto tal que su velocidad es nula. Tomando dicho punto como origen de coordenadas, tenemos
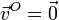
de forma que la velocidad instantánea de cada punto se reduce a
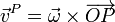
Esta forma del campo de velocidades posee una serie de propiedades que lo identifican como movimiento de rotación:
- Existe una línea recta (eje de rotación) cuyos puntos poseen velocidad nula
- La velocidad de cualquier otro punto es perpendicular al eje de rotación.
- Todos los puntos a la misma distancia del eje poseen la misma celeridad.
- La celeridad de cada punto es proporcional a su distancia al eje.
- El sentido de las velocidades cumple la regla de la mano derecha respecto al vector
 .
.
Veamos cada una de ellas por separado:
2 Eje instantáneo de rotación
De la expresión de la velocidad vemos de forma inmediata que el origen de coordenadas posee velocidad nula
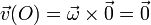
pero no es el único. Consideremos los puntos de la recta que pasa por el origen y posee la dirección dada por 
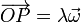
Para todos estos puntos se cumple
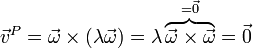
Por tanto, existe toda una recta de puntos en reposo. A esta recta se la denomina eje de rotación (o eje de giro). Su dirección es la del vector velocidad angular  .
.
3 Movimiento plano
Al tratarse de un producto vectorial
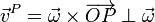
esto quiere decir que la velocidad en cada punto es perpendicular al eje de rotación y por tanto se encuentra contenida en un plano perpendicular a dicho eje.
Más aun, si consideramos dos puntos situados sobre la misma vertical (entendida como la dirección del eje de rotación)
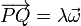

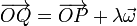
entonces la velocidad en estos dos puntos es exactamente la misma
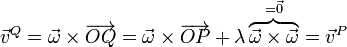
Por tanto, no solo la velocidad de todos los puntos situados en un plano perpendicular al eje de giro está contenida en dicho plano. Si tomamos planos paralelos la distribución de velocidades es idéntica en todos ellos.
4 Dependencia con la distancia
Tomando el módulo del producto vectorial obtenemos la celeridad de cada punto
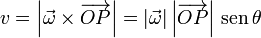
pero

siendo d la distancia al eje de giro. Por tanto, todos los puntos que se encuentren a la misma distancia del eje tienen la misma celeridad y además ésta es proporcional a la distancia al eje, esto es, un punto situado al doble de distancia que otro se mueve el doble de rápido.
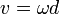
Dado que esta relación es la misma que se tiene para un movimiento circular, a ω se la denomina velocidad angular y a  el vector velocidad angular.
el vector velocidad angular.
5 Regla de la mano derecha
Por último, para el sentido de las velocidades, consideramos los puntos situados sobre una circunferencia contenida en un plano perpendicular al eje de giro y con centro en éste. Las velocidades de todos estos puntos están contenidas en el plano, sus direcciones son perpendiculares al eje de giro y al vector de posición radial, sus módulos son iguales, y su sentido viene dado por la regla de la mano derecha. Es tal que si nuestros dedos siguen el sentido de las velocidades, el pulgar indica el sentido de la velocidad angular.
6 La trayectoria NO es una circunferencia
Al estudiar el movimiento de rotación y describir las velocidades según la ley
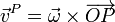
se puede adquirir la idea errónea de que las partículas del sólido describe un movimiento circular. Eso NO es correcto.
Lo que hemos hecho es describir la distribución instantánea de velocidades, esto es, que velocidad tiene cada punto del sólido en un instante dado, pero no hemos analizado cómo se mueve cada punto a lo largo del tiempo (en términos llanos, hemos tomado una fotografía, no una película de vídeo).
Puesto que 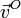 y
y  son vectores variables en el tiempo, el movimiento de una partícula puede ser extremadamente complicado.
son vectores variables en el tiempo, el movimiento de una partícula puede ser extremadamente complicado.
Consideremos el caso de un cilindro que rueda sobre el suelo. La línea de contacto esta formada por puntos con velocidad nula y por tanto se trata de un eje instantáneo de rotación. El cilindro está efectuando una rotación pura instantánea en torno a esta línea de contacto (y no respecto al eje del cilindro, como podría pensarse), pero la trayectoria de cada punto del cilindro no es una circunferencia, sino una cicloide (técnicamente, para los puntos que no son de la superficie exterior es una hipocicloide).
La razón es que aunque instantáneamente esté rotando en torno a esta línea, el eje de rotación va cambiando en el tiempo.
Otro ejemplo lo da una peonza. Su punto de apoyo puede considerarse fijo y el movimiento en cada instante es una rotación en torno un eje que pasa por este punto, pero, salvo en el caso particular de una peonza puramente vertical, la peonza experimenta movimientos de precesión (su eje instantáneo de rotación va rotando en torno a la vertical) y nutación (el eje oscila, subiendo y bajando) por lo que la trayectoria de una partícula de la peonza puede ser extremadamente complicada.
7 Movimiento con un punto fijo
Supongamos el caso particular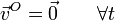
En este caso tenemos un punto O para el cual la velocidad es siempre nula y, por tanto, se encuentra permanentemente en reposo.
El movimiento del sólido es, en cada instante una rotación en torno a un eje que pasa por este punto.
No podemos asegurar que haya más puntos permanentemente en reposo, ya que la orientación del eje de giro puede cambiar con el tiempo haciendo que los puntos instantáneamente en reposo sean diferentes en cada momento.
El ejemplo típico de movimiento de un sólido con un punto fijo es el balanceo de una peonza o de un giróscopo
8 Movimiento con un eje fijo
Supongamos el caso aun más restrictivo
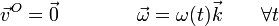
esto es, la velocidad angular, aunque variable en módulo, posee siempre la misma dirección.
En este caso, el eje de rotación es siempre el mismo y todos sus puntos están permanentemente en reposo. Se dice entonces que tenemos un movimiento con un eje fijo (eje permanente de rotación), y que el sólido es un rotor.
Este es el típico movimiento de un sólido ensartado a un eje permanente. Para este caso, sí es cierto que la trayectoria de los diferentes puntos es una circunferencia (o un arco de circunferencia).
Un ejemplo es el de un péndulo cuya barra es rígida y por tanto de longitud constante. La lenteja del péndulo efectúa un movimiento que, aunque oscilante, es de rotación en torno a un eje fijo.






